 |
Кинетическая энергия тела. вращающегося вокруг неподвижной оси?
|
|
|
|
Работа внешних сил при вращении твердого тела вокруг неподвижной оси определяется действием момента Mz этих сил относительно данной оси. Если силы таковы, что их момент Mz=0, то работы они не производят.
Из следует выражение для мощности внешних сил 
, вызывающих вращение вокруг неподвижной оси. Учитывая, что 
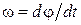, получим:
Кинетическая энергия котящегося тела?
Если тело катится (шар, колесо, и т.д.), то его энергия движения складывается из энергии вращения вокруг оси, проходящей через центр масс и энергии поступательного движения, т.е. для тела массы 
можно записать:
;
Формула справедлива для произвольного движения, поскольку его можно разложить на совокупность вращения относительно оси инерции и поступательного движения.
Какие колебания называются гармоническими?
.Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:
x(t)=A sin(ωt+φ)
, x(t)=A cos(ωt+φ)
где х — значение изменяющейся величины, t — время, остальные параметры — постоянные: А — амплитуда колебаний, ω — циклическая частота колебаний, (ωt+φ) — полная фаза колебаний, φ 
— начальная фаза колебаний.
Скорость материальной точки, совершающей гармонические колебания?
Скорость точки, совершающей гармонические колебания, определяется формулой:
Ускорение материальной точки, совершающей гармонические колебания?
- дифференциальное уравнение гармонических колебаний. Его решение описывает колебательное движение материальной точки, происходящее под действием квазиупругой силы в отсутствии сил сопротивления.
|
|
|
Смещение Хот положения равновесия при незатухающих колебаниях?
51.Пружинный маятник (определение, период колебаний)?
Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.
Период колебаний пружинного маятника вычисляется по формуле:
э
Полная механическая энергия колеблющейся точки при незатухающих колебаниях?
Свободными или собственными называются колебания, которые совершает система около положения равновесия после того, как она каким-либо образом была выведена из состояния устойчивого равновесия и представлена самой себе.
Как только тело (или система) выводится из положения равновесия, сразу же появляется сила, стремящаяся возвратить тело в положение равновесия. Эта сила называется возвращающей, она всегда направлена к положению равновесия, происхождение ее различно:
а) для пружинного маятника - сила упругости;
б) для математического маятника - составляющая сила тяжести.
Свободные или собственные колебания - это колебание, происходящие под действием возвращающей силы.
Если в системе отсутствуют силы трения, колебания продолжаются бесконечно долго с постоянной амплитудой и называются собственными незатухающими колебаниями.
Пружинный маятник - материальная точка массой m, подвешенная на абсолютно упругой невесомой пружине и совершающая колебания под действием упругой силы.
Дифференциальное уровнение затухающих гармонических колебаниях?
Коэффициент затухания?
Коэффициент затухания - это постепенное ослабевание собственных колебаний, обусловленное потерями энергии колебательной системой и приводящее к уменьшению амплитуды колебаний.
55.Смещение Ч от положения равновесия при затухающих колебаниях?
|
|
|
56. Амплитуда затухающих колебаний?
Затуханием колебаний называется постепенное уменьшение амплитуды колебаний с течением времени, обусловленное потерей энергии колебательной системой.
Собственные колебания без затухания – это идеализация. Причины затухания могут быть разные. В механической системе к затуханию колебаний приводит наличие трения. Когда израсходуется вся энергия, запасенная в колебательной системе, колебания прекратятся. Поэтому амплитуда затухающих колебаний уменьшается, пока не станет равной нулю.
Затухающие колебания, как и собственные, в системах, разных по своей природе, можно рассматривать с единой точки зрения – общих признаков. Однако, такие характеристики, как амплитуда и период, требуют переопределения, а другие – дополнения и уточнения по сравнению с такими же признаками для собственных незатухающих колебаний. Общие признаки и понятия затухающих колебаний следующие:
· Дифференциальное уравнение должно быть получено с учетом убывания в процессе колебаний колебательной энергии.
· Уравнение колебаний – решение дифференциального уравнения.
· Амплитуда затухающих колебаний зависит от времени.
· Частота и период зависят от степени затухания колебаний.
· Фаза и начальная фаза имеют тот же смысл, что и для незатухающих колебаний.
Декремент затухания?
58. Логарифми́ческий декреме́нт колеба́ний (декреме́нт затуха́ния;?
Логарифми́ческий декреме́нт колеба́ний (декреме́нт затуха́ния; от лат. decrementum — «уменьшение, убыль») — безразмерная физическая величина, описывающая уменьшение амплитуды колебательного процесса и равная натуральному логарифму отношения двух последовательных амплитуд колеблющейся величины x в одну и ту же сторону:
Добротность?
Добро́тность — параметр колебательной системы, определяющий ирину резонанса и характеризующий, во сколько раз запасы энергии в системе больше, чем потери энергии за время изменения фазы на 1 радиан. Обозначается символом Q. Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.
|
|
|
60. Какие колебания называются вынужденными?
ОПРЕДЕЛЕНИЕ: вынужденными называются такие колебания, которые возникают в колебательной системе под действием внешней периодически изменяющейся силы.
|
|
|
