 |
1. 3. Задание 3. Итак, зададим плоскость боковой грани АВС проекциями названных точек, рис. 1. 5. Общие рекомендации
|
|
|
|
1. 3. ЗАДАНИЕ 3
Последовательность выполнения задания представлена на рис. 4.
Требуется построить следы плоскости боковой грани АВС заданной пирамиды. Напомним [3], что след плоскости – это прямая пересечения заданной плоскости с плоскостью проекций. Плоскоcть общего положения пересекается и с фронтальной П2 (V), и с горизонтальной П1 (H) плоскостями проекций, поэтому и следов будет два: a1 и a2. Если плоскость занимает особое (частное) положение в пространстве, то она может иметь единственный след. Например, горизонтальная плоскость имеет единственный след на плоскости проекций П2 (V) в виде горизонтальной прямой.
Итак, зададим плоскость боковой грани АВС проекциями названных точек, рис. 4, а.
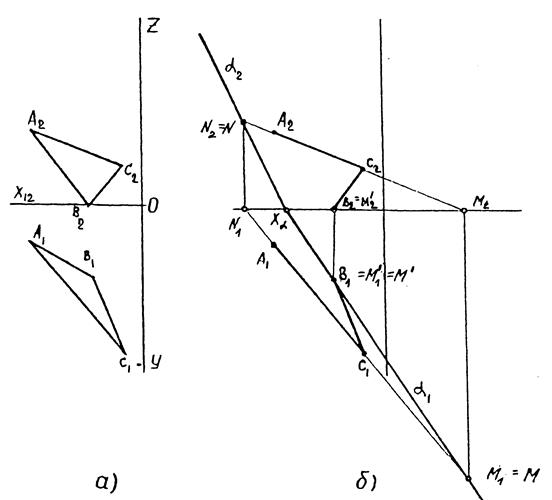
Рис. 4
Чтобы построить след плоскости, достаточно построить следы двух любых прямых, принадлежащих этой плоскости, и соединить их одноименные проекции. Выбираем прямые АС и ВС.
Строим горизонтальный след прямой АС – точку М1 пересечения указанной прямой с плоскостью П1 (H), рис. 4, б. Горизонтальный след прямой ВС совпадает с проекцией В1, поскольку точка В расположена непосредственно на горизонтальной плоскости проекций. Соединяя проекции М1 и М1`, строим горизонтальный след a1 плоскости боковой грани АВС.
Описанные построения могут быть представлены стандартными обозначениями:
МÎ (АС)LМÎ П1,
где Î - принадлежит;
L - объединение «и».
Запись означает: точка М принадлежит прямой АС и одновременно точка М принадлежит плоскости П1 (Н).
Аналогично читается вторая строка на рис. 1:
М`Î (AB)LM`Î П1.
Следующая строка показывает, что прямая (след) включает (Ì ) точки М и М` в плоскости П1(Н):
a1Ì (М, М`)Ì П1.
|
|
|
Точка пересечения горизонтального следа a1 с осью ОХ обозначена Хa (рис. 4, б). Очевидно, что для построения фронтального следа a2 достаточно построить только один фронтальный след любой из прямых, принадлежащих заданной плоскости боковой грани АВС. Например, прямой АС на рис. 4, б. След N=N2 строят по схеме, приведенной для точки М.
Соединяя точки Хa и N2, строят искомый фронтальный след a2 плоскости боковой грани АВС.
1. 4. ЗАДАНИЕ 4
Последовательность выполнения задания представлена на рис. 5.
Требуется построить плоскость, параллельную плоскости боковой грани АВС (a1, a2) и проходящую через вершину пирамиды D. Исходные данные для этой задачи представлены на рис. 5, а.
Если искомая плоскость параллельна заданной, то ее следы параллельны следам заданной плоскости (a1, a2). Поэтому достаточно построить единственную точку на пересечении искомой плоскости с любой из плоскостей проекций П1(H) либо П2(V)) и задача будет решена.

Рис. 5
Построим в точке D горизонталь h [3]. Очевидно, что ее проекция h1 будет обязательно параллельна следу a1, иначе нарушаются условия параллельности плоскостей (рис. 5, б).
Таким образом, легко строится точка 1(11, 12) пересечения горизонтали h с фронтальной плоскостью проекций П2 (V). Это и есть искомая точка, через которую должны быть проведены следы b2 и далее b1 искомой плоскости:
h'DLh1||a1;
12Î b2Lb2||a2, b1||a1.
Аналогичные построения могут быть выполнены с помощью фронтали f (f1, f2), проведенной через точку D. На рис. 1 приведены оба варианта построений. При выполнении заданий студент должен воспользоваться либо построением горизонтали h, либо фронтали f. Пояснения к рещению задачи 4 даются только для выбранного варианта решения.
1. 5. ОБЩИЕ РЕКОМЕНДАЦИИ
Как видно из примера рис. 1, задачи 3 и 4 компонуются на одном чертеже. Полученные решения необходимо выделить цветными карандашами. Например, лучи a2 и a1 – красным, b2 и b1- синим.
|
|
|
Измерения координат необходимо выполнять в натуральном масштабе миллиметровой шкалы.
В случае необходимости задачи 3 и 4 могут быть представлены на различных чертежах аналогично рис. 4, б и 5, б.
В отдельных вариантах следы прямых при построениях могут выходить за пределы формата. В этом случае необходимо воспользоваться временно зафиксированным вспомогательным листом писчей бумаги. Оставшиеся на формате линии обводят в соответствии с предложенной схемой.
|
|
|


