 |
Сложение и вычитание положительных и отрицательных чисел
|
|
|
|
ПРИЗНАКИ ДЕЛИМОСТИ
| Признак делимостина | Число делится «на», если | Делятся | Не делятся |
| оно оканчивается чётной цифрой (0,2,4,6,8) | 148; 10006; 74; 270 | 43; 1225; 1007 | |
| оно оканчивается нулём | 20; 69800; 430 | 255; 6631; 14; 87 | |
| оно оканчивается 0 или 5 | 2205; 980; 70; 9875 | 2201; 987; 74; 552 | |
| сумма цифр числа делится на 3 | 411(4+1+1=6); 1002; 81; 111000 | 751; 33800; 80821 | |
| сумма цифр числа делится на9 | 1260; 6039; 70704 | 111115; 120; 30305 |
РАЗЛОЖЕНИЕ НА ПРОСТЫЕ МНОЖИТЕЛИ
Разложить число на простые множители – значит представить его в виде произведения простых чисел.
75 = 5∙5∙3
1) 28 = 2∙2∙7; 2) 363 = 3∙11∙11; 3) 264 = 2∙2∙2∙3∙11
Ход работы в примере 3): 264 2
264:2 = 132 132 2
13 2:2 = 66 66 2
66: 2 = 33 33 3
33:3 = 11 11 11
11:1 1= 1 делители – только простые числа
НОК и НОД (наименьшее общее кратное и наибольший общий делитель)
НОД (63и98) = 7 НОД(120и45) = 5∙3=15
63 3 98 2 120 5 45 5
21 3 49 7 24 2 9 3
7 7 7 7 12 2 3 3
63=3∙3∙7 98=2∙7∙76 2 120=5∙2∙2∙2∙3; 45= 5∙3∙3
3 3
НОК(15и20) = (5∙3)∙ 2 ∙ 2 =60 НОК(12и40) = (2∙3∙2)∙ 5 ∙ 2 =120
15 5 20 2 нетвразложе - 12 2 40 2 нет враз-
3 3 10 2 нии 15 6 2 - 5 ложении12
5 5 3 3 4 2
2 2
СОКРАЩЕНИЕ ДРОБЕЙ
Чтобы сократить дробь, нужно и числитель и знаменатель разделить на одно и то же число.
(сократили на 5)
= 
(сократили на 2)
= 
(сокр. на 10)= 
(сокр. на 2)
, , ─ несократимые дроби
ПРИВЕДЕНИЕ ДРОБЕЙ К ОБЩЕМУ ЗНАМЕНАТЕЛЮ
Любые две дроби можно привести к общему (одинаковому) знаменателю. Обычно дроби приводят к наименьшему общему знаменателю (НОЗ). НОЗ = НОК знаменателей
1) 
и 
; а) НОК(9и 6)=18; б) 18:9=2, 18:6=3 (2 и 3 – дополнительные мно –
Жители)
В) умножаем на дополнительные множители и числители и
|
|
|
Знаменатели данных дробей.
Ответ: и → 
и 
2) 
и 
; а) НОК(12 и 15)=60; б)60:12=5, 60:15=4 (5 и 4 – дополн. множ.)
В) см.пример 1.
Ответ: и → 
и 
СРАВНЕНИЕ, СЛОЖЕНИЕ И ВЫЧИТАНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ
Чтобы сравнить, сложить или вычесть обыкновенные дроби, надо:
· привести дроби к общему знаменателю;
· сравнить, сложить или вычесть числители новых дробей, оставляя их знаменатели без изменения.
1. Сравнить: 
и 
;а) НОЗ (9и7)=63; б) 
= 
; 
= 
; в) 
› → 
› 
2.
+ 
(НОЗ(10и15) = 30 ← в уме) = 
+ 
= 
Вычислить: 
– 
(НОЗ(12и8) = 24 ← в уме) = 
– 
= 
ЗАПИСЬ: 
+ 
= 
= 
= 
СЛОЖЕНИЕ И ВЫЧИТАНИЕ СМЕШАННЫХ ЧИСЕЛ
1. 
+ 
= 
= 
= 
← в ответе дробь должна быть правильной
2. 
–1 
= 
= 4 = 4 ← в ответе дробь должна быть несокра-
Тимой
3. 3 
– 
= 
←? (9 
11): занимаем у 2 целых 1 и дробим её на 
,которые добавляем к дробной части, имеем: 
= 
= 
1 = 
= 
= …… = 
= …… = 
= …… = 
= ….
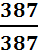УМНОЖЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ
· Для умножения обыкновенных дробей нужно перемножить их числители и их знаменатели.
· Если возможно сокращение – его надо выполнить, это облегчит вычисления .
· При умножении смешанных и целых чисел их заменяют неправильными дробями.
1. 
∙ 
= 
= 
2. 2 
∙ 
= 
= 
= 
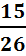= 1 
3. 7 ∙ = 
∙ = 
= 4 
ДЕЛЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ
Деление обыкновенных дробей можно заменить умножением на «перевёрнутую» дробь.
Шаги деления обыкновенных дробей:
1. преобразовать пример: 
: (все компоненты – дроби)
2. заменить: : 
= ∙ 
Выполнить умножение
1) : 
= 
∙ 
= 
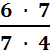= = 1 ;
2) 
: 6 
= 
: 
= ∙ 
= 
= 
НАХОЖДЕНИЕ ДРОБИ ОТ ЧИСЛА
| всё целое (знаем) |
| дробь (?) |
Задача. В книге 140 страниц. Андрей прочитал 0,3 этой книги. Сколько страниц прочитал Андрей?
|
|
|
Решение
0,3 от 140 стр.; 140 ∙ 0,3 = 42 (стр.)
Ответ: Андрей прочитал 42 страницы.
НАХОЖДЕНИЕ ЧИСЛА ПО ЕГО ДРОБИ
| всё целое (?) |
| дробь (знаем) |
Задача. Девочка прошла на лыжах 300 метров, что составляет 
дистанции. Какова длина дистанции?
Решение
300 м сост. дистанции; 300: = 
∙ 
= 
= 800 (м)
Ответ: длина дистанции 800 метров.
ОТНОШЕНИЯ И ПРОПОРЦИИ
1) 2: 48; 36: 1,8; х: 15 - отношения.
2) Пропорция – равенство двух отношений.
3) 12: 6 = 100: 50 12 и 50 – крайние члены
И 100 – средние члены
= 
4) Основное свойство пропорции: е сли пропорция верна, то произведение крайних членов равно произведению средних членов пропорции: 12: 6 = 100: 50; → 12 ∙ 50 = 6 ∙ 100 = 600;
5) Решение уравнений
= 
10: Х = 2,5: 5
0,4 ∙х = 2∙ 5 2,5Х = 10 ∙ 5
0,4х = 10; х = 10: 0,4 = 100:4=25; Х = 25 2,5Х = 50; Х = 50: 2,5 = 500: 25; Х = 20
ДЛИНА ОКРУЖНОСТИ. ПЛОЩАДЬ КРУГА.
C– длина окружности; S – площадь круга;
∏(пи) ≈ 3,1415926536… (3,14);R(r)-радиус;
C = 2∏RS = ∏ 
Задача Найти длину окружности и площадь круга с радиусом5 см.
Решение
1. 
r = 2 ∙ 3,14 ∙5 = 6,28 ∙ 5 = 31,4(см)
2. 
= 3,14 ∙ 
= 3,14 ∙ 25 = 78,5( 
)
Окружность – линия, Круг – часть плоскости
| КРУГ |
КООРДИНАТЫ НА ПРЯМОЙ. ПРОТИВОПОЛОЖНЫЕ ЧИСЛА. МОДУЛЬ ЧИСЛА.
| -5 |
| -1 |
| -2 |
| -3 |
| -4 |
| A |
| B |
| C |
1.
В(-5); А(2); С(3,4) – координаты точек
Противоположные числа: 2 и-2; 5 и-5; -135 и 135; -2,3 и 2,3
3. а - модуль числа а
│ а │ = а, если а ≥ 0 → │9│ = 9; │138│ = 138; │0│ = 0
│ а │ = -а, если а ≤ 0 → │-5│ = 5; │-18│ = 18
Модуль числа не может быть отрицательным!
СРАВНЕНИЕ ЧИСЕЛ
| -5 |
| -1 |
1. Из двух чисел всегда больше то, которое расположено на числовой прямой правее:
21 › -40; 18 › 11; -2 › -2339.
2. Любое положительное число всегда больше
отрицательного: 0,12 › -743; 1 › -5
3. Любое положительное число больше нуля, а любое отрицательное меньше нуля: 25 › 0; 0 ‹ 987; 0 › -45; -2,47 ‹ 0
4. Из двух отрицательных чисел больше то, у которого модуль меньше:
-287 ‹ -5; -18 › -35; -100 ‹ -1
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ
1. Чтобы сложить два отрицательных числа, нужно сложить их модули и в ответе поставить знак «-«:
|
|
|
(-5) + (-11) = -16; -100 + (2,9) = -102,9
2. Чтобы сложить два числа с разными знаками, нужно из большего модуля вычесть меньший и в ответе поставить знак слагаемого с большим модулем:
25 + (- 8 ) = 17 |25| › |-8| → в ответе знак «+»
-25 + 8 = -17; |-25| › |8| → в ответе знак «-«
3. Чтобы из одного числа вычесть другое, нужно к уменьшаемому прибавить число, противоположное вычитаемому: а) -6 – 10 = -6 + (-10) = -16; б) 2 – (-3) = 2 + 3 = 5; в) -1 – (-5) = -1 + 5 = 4;
|
|
|
