 |
Решение задач на определение кинематических характеристик вращательного движения твердого тела.
|
|
|
|
Задачи на вращение твердого тела вокруг неподвижной оси можно разбить на два типа.
Первый тип задач – дано уравнение вращения твердого тела, требуется найти кинематические характеристики вращательного движения: угловую скорость, угловое ускорение, скорость и ускорение заданной точки твердого тела.
Задачи этого типа следует решать, придерживаясь следующих правил:
1. Выбрать систему координат, направив одну из осей координат на оси вращения;
2. записать уравнение вращения твердого тела  ;
;
3. Определить угловую скорость вращения тела:  ;
;
4. Найти угловое ускорение вращения твердого тела:  ;
;
5. Определить скорость точки твердого тела, вращающегося вокруг неподвижной оси.
6. Найти нормальное и касательное ускорения точки  ,
,  ;
;
7. Определить полное ускорение точки по величине и направлению.
Второй тип задач представляет собой обратную задачу. Заданы кинематические характеристики: угловая скорость или угловое ускорение, требуется найти уравнение вращения твердого тела, скорость и ускорение точек твердого тела.
В этом случае алгоритм решения задачи будет таким:
1. Определить проекцию угловой скорости на ось вращения, для чего нужно проинтегрировать дифференциальное уравнение  ;
;
2. Зная угловую скорость, как функцию времени, определить уравнения вращения твердого тела;
3. Найти величину скорости и нормального ускорения точки.
4. Найти величину касательного ускорения очки;
5. Определить полное ускорение точки.
Задача №17 (Мещерский И.В. 13.4)
Тело начинает вращаться равноускоренно из состояния покоя, делая 3600 оборотов за первые две минуты. Определить угловое ускорение.
Решение: Дано n = 3600 оборотов
t = 2 мин. = 120 с.
Определить ε.
|
|
|
1. Запишем уравнение движения, зная, что тело движется равноускоренно  . В нашем случае
. В нашем случае  ,
,  (вращательное движение тела начинается из состояния покоя).
(вращательное движение тела начинается из состояния покоя).
2. Определим угловое ускорение  :
:  , здесь
, здесь  . Подставляя значения
. Подставляя значения  и t, получим
и t, получим

Ответ:  .
.
Задача №18 (Мещерский И.В. 13.7)
Колесо, имеющее неподвижную ось, получило начальную угловую скорость  , сделав 10 оборотов. Оно вследствие трения в подшипниках остановилось. Определить угловое ускорение εколеса, считая его постоянным.
, сделав 10 оборотов. Оно вследствие трения в подшипниках остановилось. Определить угловое ускорение εколеса, считая его постоянным.
Дано: 
 оборотов
оборотов
Определить ε.
Решение.
1. Определим закон вращательного движения колеса, зная, что оно вращается равнозамедленно  ;
;
2. Для определения углового ускорения ε воспользуемся формулой  , так как
, так как  (колесо остановилось), то
(колесо остановилось), то  ;
;
3. Найдем угол, описанный телом за 10 оборотов  ;
;
4. Определим время вращения тела, используя закон движения  , получим
, получим  . Подставляя численные значения
. Подставляя численные значения  и
и 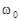 , найдем t
, найдем t
 сек.
сек.
5. Зная, что  , найдем
, найдем  .
.
Ответ:  .
.
Задача №19 (Мещерский И.В. 13.13)
Моховое колесо радиуса r =0,5 м вращается равномерно вокруг своей оси; скорость точек обода  2 м/с
2 м/с
Сколько оборотов в секунду делает колесо

Дано: r =0,5м
 2 м/с
2 м/с
Определим n об/мин.
Решение:
1. Определим угловую скорость вращения колес, пользуясь формулой
 ;
;  ;
;  рад/сек
рад/сек
3. Найдем число оборотов в минуту, которое делает колесо, имея угловую скорость 4 рад/сек.
 ;
; 
Подставляя численные значения 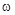 и
и  , получим
, получим
 об/мин.
об/мин.
Ответ: колесо делает 38,2 оборотов в минуту.
Задача №20 (Мещерский И.В. 13.16)
Найти горизонтальную скорость v, которую надо сообщить телу находящемуся на экваторе, для того, чтобы оно двигалось равномерно вокруг Земли по экватору в особых направляющих, имея ускорение q.
Определить также время T, чтобы оно вернулось назад.
Радиус Земли Rз =637*106 см, q=978 см/с2
Дано: R=637*106 см,
Q=978
Определить: V и T.
Решение:
1. Такое движение тел равномерно на тело действует только нормативная составляющая ускорения Wn=V/R=mg.
|
|
|
Отсюда V =  ,V =
,V =  см/с=7,89 км/с.
см/с=7,89 км/с.
2. За один оборот тело проходит путь S=2  R. С другой стороны S = VT, 2
R. С другой стороны S = VT, 2  R = VT,
R = VT, 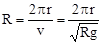
 часа.
часа.
Ответ: V=7,89 км/с, T=1,4 часа.
Задача №21 (Мещерский И.В. 13.12)
Определить скорость v и ускорение w точки Ленинграда, принимая во внимание только вращение Земли вокруг оси. Широта Ленинграда φ=600 , радиус земли R=6370 км.
Дано: φ=600
R=6370 км
Определить: V и W.
Решение: 1. Определим скорость точки по формуле
 ,
,
где 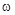 - угловая скорость вращения Земли, она определяется по формуле
- угловая скорость вращения Земли, она определяется по формуле  рад/сек,
рад/сек,
 r-расстояние точки от оси вращения
r-расстояние точки от оси вращения
 .
.
Подставляя значения 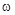 и
и 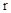 в формулу для вычисления скорости точки, будем иметь
в формулу для вычисления скорости точки, будем иметь 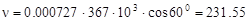 2.Определим ускорение точки
2.Определим ускорение точки 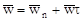 , т.к. вращение земли равномерное, то
, т.к. вращение земли равномерное, то 
 ;
;  м/с2.
м/с2.
Ответ:  м/с,
м/с, 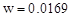 м/с2.
м/с2.
Задачи на преобразование простейших движений твердого тела.
Задача №22 (Мещерский И.В. 13.18)
Вал радиуса R=10 см. приводится в движение гирей Р, которая перемещается вертикально по закону X = 100 t2 см. Определить угловую скорость и угловое ускорение вала ε, а также ускорение точки вала, лежащей на ободе в момент времени t.
Дано: R=10 см.
X=100 t2 см.
Определить: ω и ε и w.
Решение: 1. Определим скорость точки М 
 2. Найдем угловую скорость вращения вала по формуле
2. Найдем угловую скорость вращения вала по формуле  , т.к. вал приводится в движение из состояния покоя, то
, т.к. вал приводится в движение из состояния покоя, то  . Угловое ускорение, входящее в формулу, определим из условия
. Угловое ускорение, входящее в формулу, определим из условия  ,
,  ,
, 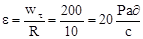 . Следовательно угловая скорость вращения будет
. Следовательно угловая скорость вращения будет  .
.
3. Определим ускорение точки М по формуле 

Полное ускорение точки M будет

Ответ:  рад/сек,
рад/сек,  рад/сек,
рад/сек,  см/с2 .
см/с2 .
Задача №23 (Мещерский И.В. 14.10)
Ведущий вал Iфрикционной передачи вращается с угловой скоростью ω=20л рад/с и на ходу передвигается (направление указано стрелкой) так,что расстояние d меняется по закону d=(10-0,5t)см (t в секундах)
Определить:
1. Угловое ускорение вала II как функцию ускорения d.
2. Ускорение точки m обода колес B в момент когда d=r.
Даны радиусы фрикционных колес r =5см, R=15см.
Дано: ω=2π рад/с,
d=(10-0,5t) см
r=5 см
R=15см
 Определить: w и ε.
Определить: w и ε.
Решение: 1. Определим угловую скорость вращения вала II, исходя из того, что линейные скорости вала в точке К равны  отсюда
отсюда 
2.Определим угловое ускорение вращение вала II 
Здесь d величина переменная

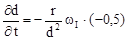
 рад/с.
рад/с.
3.Найдем полное ускорение

где  ;
;  ;
;  . Для d=r
. Для d=r  ,
,
 ,
,  см/с2.
см/с2.
Ответ:  ,
,  см/с2.
см/с2.
Задача №24 (Мещерский И.В. 14.16)
|
|
|
 Найти закон движения и построить график возвратно-поступательного движения стержня АВ, если задано профиля кулака
Найти закон движения и построить график возвратно-поступательного движения стержня АВ, если задано профиля кулака  см, 0<φ<2π. Кулак вращается с угловой скоростью
см, 0<φ<2π. Кулак вращается с угловой скоростью  .
.
Дано:  см,
см,
 ,
, 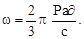
Определить: x(t)=x.
Решение: 1. Определим закон изменения угла φ. Так как кулак вращается равномерно, то


при t=0, φ=0, c=0.
Следовательно, 
2. Найдем закон изменения r в зависимости от t.

Так как стержень АВ совершает поступательное движение, то x=20+10t.
3.  Определим время за которое точка А возвращается прежние положение при изменение угла φ.
Определим время за которое точка А возвращается прежние положение при изменение угла φ.

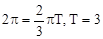 сек.
сек.
Ответ: x = 20+10t.
|
|
|


