2.6. Цепь переменного тока с индуктивностью

2. 6. Цепь переменного тока с индуктивностью

Условное обозначение индуктивности на рис. 2. 8.

                            

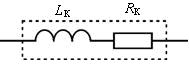
Рис. 2. 8                                                                                Рис. 2. 9

 

Катушка с проводом кроме свойства создавать магнитное поле обладает активным сопротивлением R.

Условное обозначение реальной индуктивности на рис. 2. 9.

Единицей измерения индуктивности является генри (Гн). Рассмотрим цепь (рис. 2. 10), в которой к катуш­ке индуктивности L, не обладающей активным со­противлением (R=0), приложено синусоидальное на­пряжение. Векторная диаграмма для этой цепи изображена на рис. 2. 11.

            

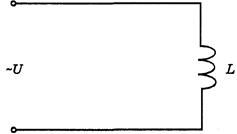
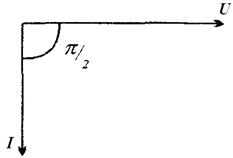
Рис. 2. 10                                                                       Рис. 2. 11

 

Протекающий через катушку переменный ток создает в ней ЭДС самоиндукции e_L.

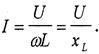                                                     2. 3

Соотношение (2. 3) представляет собой закон Ома для цепи с идеальной индуктивностью, а величина x_L называется индуктивным сопротивлением.

Мощность, потребляемая цепью с чис­то и индуктивным сопротивлением, изменяется по закону синуса с удвоенной частотой (рис. 2. 12).

 

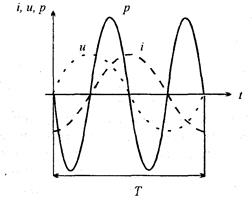Положительные значения мощности соответству­ют потреблению энергии катушкой, а отрицательные, возврату запасенной энергии обратно источнику.

Средняя за период мощность равна нулю. Мы видим, что цепь с индуктивностью мощности не потребляет – это реактивная нагрузка. В этой цепи происходит лишь перекачивание электри­ческой энергии от источника в катушку и обратно.

Рис. 2. 12

2. 7. Цепь переменного тока с активно-индуктивной нагрузкой

Теперь рассмотрим электрическую цепь (рис. 2. 13), в которой через катушку индуктивности L, обладаю­щую активным сопротивлением R, протекает пере­менный ток:

I = I₀ sin ω t                                                  2. 4

Через катушку и через резистор протекает один и тот же ток, поэтому в качестве основного выберем вектор тока, и будем искать вектор напряжения, при­ложенного к этой цепи.

Рис. 2. 13

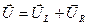                                                                 2. 5

 Напряжение, приложенное к цепи, равно векторной сумме падений напряжений на катушке индуктивности и на резисторе.

Из векторной диаграммы видим, что напряжение на индуктивности опережает ток на 90^о:

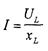                                                        2. 6

Закон Ома для цепи с идеальной индуктив­ностью (т. е. не обладающей активным сопротивле­нием) выглядит так: 2. 6, величина x_L называется индуктивным сопротивлением. Построив векторы I, U_R и U_L и вос­пользовавшись формулой (2. 5), найдем вектор U.

 Векторная диаграмма для этой цепи показана на рис. 2. 14.

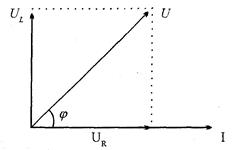
Рис. 2. 14

Величина

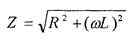                                                   2. 7

называется полным сопротивлением цепи. Сдвиг по фазе   между током и напряжением также определяется из векторной диаграммы. В данной цепи угол сдвига фаз между током и напряжением зависит от значений R и L и изменяется в пределах от 0 до 90^о.

Рассмотрим теперь, как изменяется со временем мощность в цепи с активно-индуктивной нагрузкой.

Мы видим, что мгновенное значение мощности имеет две составляющие: первое слагаемое – актив­ная, и второе – реактивная (индуктивная). Поэто­му средняя за период мощность не равна нулю. Соответствующая этой мощности электрическая энергия превращает­ся в активном сопротивлении R в теплоту.

 

2. 8. Цепь переменного тока с емкостью

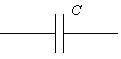
Условным обозначением емкости является символ C (рис. 2. 15)

Рис. 2. 15

 

Рассмотрим электрическую цепь, в которой пере­менное напряжение приложено к емкости С (рис. 2. 16). Векторная диаграмма показана на рис. 2. 17. Мгновенное значение тока в цепи с емкостью равно скорости изменения заряда на обкладках кон­денсатора (2. 8).

                        

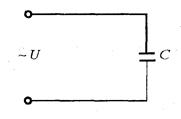
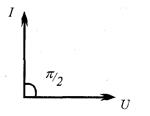
Рис. 2. 16                                                                 Рис. 2. 17

 

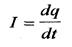                                                        2. 8

В этой цепи ток опережает напряжение на 90^о.

                                                       2. 9

Закон Ома для цепи переменного тока с емкостью (2. 9), а величина х_с называется емкостным сопротивлением. Векторная диаграмма для этой цепи показана на рис. 2. 18.

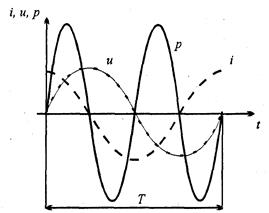
Рис. 2. 18

 

В этой цепи мгновенная мощность изменяется с удвоенной частотой (рис. 2. 18). При этом положи­тельные значения мощности соответствуют заряду конденсатора, а отрицательные – его разряду и воз­врату запасенной энергии в источник. Средняя за период мощность здесь равна нулю, поскольку в цепи с конденсатором активная мощность не потребляется, а происходит обмен электрической энергией между конденсатором и источником.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: