Главная | Обратная связь | Поможем написать вашу работу!

Примеры рефлексивных отношений

Существуют два основных способа задания множеств: перечисление и описание его элементов. Перечисление состоит в получении полного списка элементов множества, а описание заключается в задании такого свойства, которым элементы данного множества обладают, а все остальные нет.

4. Пересечением двух множеств называют множество, состоящее из всех общих элементов этих множеств.

Пример:
Возьмем числа 12 и 18. Найдем их делители, обозначив все множество этих делителей соответственно буквами А и B:
А = {1, 2, 3, 4, 6, 12},
B = {1, 2, 3, 6, 9, 18}.

Мы видим, что у чисел 12 и 18 есть общие делители: 1, 2, 3, 6. Обозначим их буквой C:
C = {1, 2, 3, 6}.

Множество C и является пересечением множеств А и B. Пишут это так:
А ∩B =C.

А ∩B= {1, 2, 3, 6}.

Если два множества не имеют общих элементов, то пересечением этих множеств является пустоемножество.
Пустое множество обозначают знаком Ø, а используют такую запись:

X ∩Y = Ø.

Объединение двух множеств – это множество, состоящее из всех элементов этих множеств.

Для примера вернемся к числам 12 и 18 и множеству их элементов A и B. Выпишем сначала элементы множества А, затем добавим к ним те элементы множества B, которых нет во множестве А. Мы получим множество элементов, которым обладают А и B в совокупности. Обозначим его буквой D:

D = {1, 2, 3, 4, 6, 12, 9, 18}.

Множество D и является объединением множеств A и B. Пишется это так:

D =A U B.

A U B= {1, 2, 3, 4, 6, 12, 9, 18}.

5.Декартовым произведением множеств A и B называется такое результирующее множество пар вида (x,y), построенных таким образом, что первый элемент из множества A, а второй элемент пары — из множества B. Общепринятое обозначение:

A×B={(x,y)|x∈A,y∈B}

Произведения трёх и более множеств можно построить следующим образом:

A×B×C={(x,y,z)|x∈A,y∈B,z∈C}

Примеры

1.Положим A={1,2},B={3,4}. Тогда результат декартова произведения можно записать так: A×B={(1,3),(1,4),(2,3),(2,4)}, а B×A={(3,1),(3,2),(4,1),(4,2)}

2.Если в предыдущем примере положить B=A, очевидно, что A×B=B×A={(1,3),(1,4),(2,3),(2,4)}

3.Возьмём A={x∈R|0≤x≤5},B={x∈R|5≤x≤10}. Тогда A×B={(x,y)∈R^2|0≤x≤5∧5≤x≤10}

6. Разностью множеств A и B называется множество элементов, принадлежащих A и не принадлежащих B. Обозначают A \ B и читают "разность A и B ".

Пример 1. Пусть A есть отрезок [1, 3], B - отрезок [2, 4]; тогда объединением будет отрезок [1, 4], пересечением - отрезок [2, 3], разностью A \ B - полуинтервал [1, 2), B \ A - полуинтервал (3, 4].

Пример 2. Пусть A есть множество прямоугольников, B - множество всех ромбов на плоскости. Тогда есть множество всех квадратов, A \ B - множество прямоугольников с неравными сторонами, B \ A - множество всех ромбов с неравными углами.

7. Пересечение множеств является бинарной операцией на произвольном булеане ;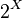

§ Операция пересечения множеств коммутативна:

§ Операция пересечения множеств транзитивна:

§ Универсальное множество является нейтральным элементом операции пересечения множеств:

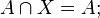
§ Таким образом булеан вместе с операцией пересечения множеств является абелевой группой;

§ Операция пересечения множеств идемпотентна:

§ Если — пустое множество, то

8. Объединение множеств является бинарной операцией на произвольном булеане

§ Операция объединения множеств коммутативна:

§ Операция объединения множеств транзитивна:

§ Пустое множество является нейтральным элементом операции объединения множеств:

§ Таким образом булеан вместе с операцией объединения множеств является моноидом;

§ Операция пересечения множеств идемпотентна:

Виды отношений

1.Бинарное отношение (двучленное отношение). Бина́рное отноше́ние в математике — двухместное отношение между любыми двумя множествами и , то есть всякое подмножество декартова произведения этих множеств: ^[1]. Бинарное отношение на множестве — любое подмножество , такие бинарные отношения наиболее часто используются в математике, в частности, таковы равенство, неравенство, эквивалентность, отношение порядка.

2. Тернарное отношение — то же, что трёхместное отношение (трёхчленное отношение).

3.Кватернарное отношение — то же, что четырёхместное отношение (четырёхчленное отношение)

10. Рефлексивное отношение в математике — бинарное отношение на множестве , при котором всякий элемент этого множества находится в отношении с самим собой.

Формально, отношение рефлексивно, если .

Свойство рефлексивности при заданных отношениях матрицей характеризуется тем, что все диагональные элементы матрицы равняются 1; при заданных отношениях графом каждый элемент х имеет петлю — дугу (х, х).

Бинарное отношение на множестве является рефлексивным тогда и только тогда, когда его подмножеством является тождественное отношение на множестве (), то есть .

Если это условие не выполнено ни для какого элемента множества , то отношение называется антирефлексивным (или иррефлексивным).

Если антирефлексивное отношение задано матрицей, то все диагональные элементы являются нулевыми. При задании такого отношения графом каждая вершина не имеет петли — нет дуг вида (х, х).

Формально антирефлексивность отношения определяется как: .