 |
Элементы комбинаторики.
|
|
|
|
Если из множества, содержащего m элементов, требуется выбрать какие-то k элементов, то возникает вопрос: сколькими способами это можно сделать и какие подмножества при этом получаются. Такие задачи называются комбинаторными, а соответствующий раздел математики – комбинаторикой.
Все формулы для подсчета числа решений в комбинаторных задачах опираются на правило произведения: если элемент X можно выбрать k способами, а элемент Y можно выбрать n способами, то пару XY можно составить kn способами.
Размещение с повторением. Из множества, содержащего m элементов, нужно выбрать k элементов, причем выбранный элемент, после того, как его взяли, вновь возвращается в исходное множество (то есть элементы в выбранном множестве могут повторяться). Пользуясь правилом произведения, получим, что каждый из k элементов может быть выбран m способами. Таким образом, общее число комбинаций равно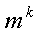 
.
Пример. Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5, 7.
Решение. Первой цифрой в числе может быть любая из четырех имеющихся. То же самое можно сказать и о последующих цифрах числа, поэтому общее число комбинаций: 
Размещение без повторений. Из множества, содержащего m различных элементов, надо выбрать упорядоченное подмножество из k элементов (k £ m), то есть такое подмножество, в котором элементы располагаются в определенном порядке, и изменение порядка элементов изменяет подмножество. Кроме этого, элементы в выбранном подмножестве не повторяются. Требуется выяснить, сколько таких комбинаций существует. По правилу произведения получаем, что первый элемент можно выбрать m способами, второй элемент – (m-1) способом, и так далее, а элемент с номером k можно выбрать (m – k + 1) способами. Следовательно, число упорядоченных k-элементных подмножеств, взятых из множества, содержащего m элементов равно m(m-1)(m-2)…(m-k+1). Такие подмножества называются размещениями из m элементов по k элементов, а их общее число можно выразить формулой 
|
|
|
Пример. Сколько различных четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, при условии. Что цифры в числе не повторяются?
Решение. Общее число комбинаций равно числу размещений из 6 элементов по 4: 
Перестановки. Пусть множество содержит m различных элементов. Рассмотрим все возможные варианты перестановок элементов этого множества. Получаемые при этом упорядоченные множества отличаются друг от друга только порядком входящих в них элементов. Такие упорядоченные множества называются перестановками. Число перестановок из m элементов равно: 
Пример. Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5. 7, если цифры в числе не повторяются?
Решение. Количество чисел равно числу перестановок из четырех элементов: 
Сочетания. Пусть из множества, содержащего m различных элементов, требуется выбрать подмножество, содержащее k различных элементов (k £ m). Получаемые при этом подмножества не упорядочены. Такие неупорядоченные подмножества называются сочетаниями. Число сочетаний из m элементов по k элементов вычисляется по формуле: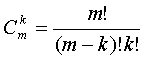 
Пример. В группе 10 студентов. Сколькими способами можно выбрать из этой группы троих студентов для участия в конференции?
Решение. Число способов равно числу сочетаний из 10 элементов по 3 элемента: 
.
18. Полином Жегалкина — многочлен над кольцом 
, то есть полином с коэффициентами вида 0 и 1, где в качестве произведения берётся конъюнкция, а в качестве сложения —исключающее или. Полином был предложен в 1927 году Иваном Жегалкиным в качестве удобного средства для представления функций булевой логики. В зарубежной литературе представление в виде полинома Жегалкина обычно называется алгебраической нормальной формой (АНФ).
|
|
|
Теорема Жегалкина — утверждение о существовании и единственности представления всякой булевой функции в виде полинома Жегалкина.
Полином Жегалкина представляет собой сумму по модулю два произведений неинвертированных переменных, а также (если необходимо) константы 1. Формально полином Жегалкина можно представить в виде
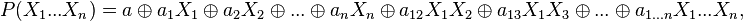
или в более формализованном виде как:
Примеры полиномов Жегалкина:
19. Конъюнкцией предикатов 
называют предикат 
определенный на том же множестве и обращающийся в истинное высказывание при тех и только тех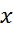 
, при которых оба предиката обращаются в истинные высказывания:
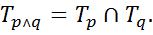
Дизъюнкцией предикатов называют предикат 
определенный на том же множестве и обращающийся в истинное высказывание при тех и только тех 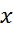, при которых хотя бы один из этих предикатов обращается в истинное высказывание:
Отрицанием предиката 
называют предикат 
определенный на том же множестве и обращающийся в истинное высказывание при тех значения 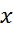, при которых обращается в ложное высказывание, т.е.
20. Импликацией предикатов называют предикат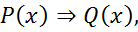 
определенный на том же множестве и обращающийся в да ложное высказыванием при тех и только тех 
при которых обращаются в истинные высказывания, а 
ложное. Согласно данному определению область ложности импликации предикатов находят по формуле
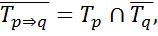
А область истинности импликации предикатов по формуле
Эквиваленцией предикатов называют предикат 
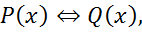
Определенный на том же множестве и обращающийся в истинное высказывание при тех и только тех 
при которых обращаются оба в истинные высказывания или оба в ложные.
Пользуясь данным определением, можно записать формулу для нахождения области истинности эквиваленции предикатов:
Последнюю формулу можно записать иначе:
21. Формула бинома Ньютона для натуральных n имеет вид 
, где 
- биномиальные коэффициенты, представляющие из себя сочетания из n по k, k=0,1,2,…,n, а "!" – это знак факториала).
К примеру, известная формула сокращенного умножения "квадрат суммы" вида 
есть частный случай бинома Ньютона при n=2.
|
|
|
Выражение, которое находится в правой части формулы бинома Ньютона, называют разложением выражения (a+b)n, а выражение 
называют (k+1) -ым членом разложения, k=0,1,2,…,n.
22. Формула де-Моргана:
23. Теория графов – это раздел дискретной математики, исследующий свойства конечных множеств с заданными отношениями между их элементами.
Граф – это конечное множество Х, состоящее из n элементов 
называемых вершинами графа, и подмножество V декартова произведения 
называемое множеством дуг.
Граф, или неориентированный граф 
— это упорядоченная пара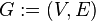 
, где 
— это непустое множество вершин или узлов, а 
— множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами.
(а значит и, , иначе оно было бы мультимножеством) обычно считаются конечными множествами. Многие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов, поскольку не все утверждения, имеющие место для конечных совокупностей, выполняются в случае бесконечных множеств.
Вершины и рёбра графа называются также элементами графа, число вершин в графе 
— порядком, число рёбер 
— размером графа.
Вершины 
и 
называются концевыми вершинами (или просто концами) ребра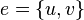 
. Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.
Два ребра называются смежными, если они имеют общую концевую вершину.
Два ребра называются кратными, если множества их концевых вершин совпадают.
Ребро называется петлёй, если его концы совпадают, то есть 
.
Степенью 
вершины называют количество инцидентных ей рёбер (при этом петли считают дважды).
Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.
Графы делятся на два типа,обычные и сложные
|
|
|
