 |
Контур с отрицательной обратной связью
|
|
|
|
Общий вид контура с отрицательной обратной связью приведен на рис 7.8.

При построении модели возникает необходимость введения различных вспомогательных переменных, отражающих промежуточные этапы определения уровней и темпов. Вспомогательные переменные обозначаются окружностью.
В отличие от контура положительной обратной связи, здесь темп потока зависит от разности DISC между фактическим и желаемым состоянием системы GL. Желаемое состояние - это цель, задаваемая извне. В данном случае величина DISC является вспомогательной переменной.
Контур отрицательной обратной связи описывается следующей системой уравнений:
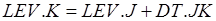 , (7)
, (7)
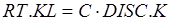 , (8)
, (8)
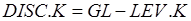 , (9)
, (9)
где LEV - уровень, RT - темп, C - константа пропорциональности, характеризующая чувствительность системы, DISC - разность между целью и уровнем.
Подставив (7.9) в (7.8) и полученное выражение в (7.7), получим:
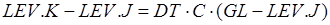 . (10)
. (10)
Используя те же обозначения, что и в п.7.1.1, и обозначив 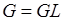 , получим аналитическое выражение для уровня
, получим аналитическое выражение для уровня
 . (11)
. (11)
Разделив обе части на D t и переходя к пределу при 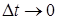 , приходим к дифференциальному уравнению
, приходим к дифференциальному уравнению
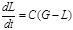 . (12)
. (12)
Проведя разделение переменных
 ,
,
получим общее решение
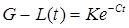 ,
,
где K - постоянная интегрирования. При начальном условии  получаем
получаем
 .
.
Таким образом, решение уравнения (7.12) при заданном начальном условии имеет вид
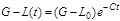 . (13)
. (13)
Из выражения (13) следует, что отклонение текущего уровня L(t) от желаемого состояния G при t ® ¥ стремится к нулю.
|
|
|
Поведение системы зависит от начального условия и показано на рис. 7.9.
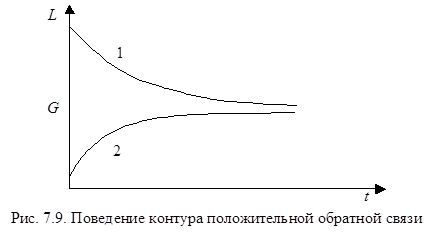
Кривая 1 соответствует случаю G < L0, а кривая 2 - случаю G > L0.
Моделирование S-образного роста
Часто поведение системы описывается S-образной или логистической кривой, показанной на рис. 7.10.

Кривая имеет два участка: начальный участок экспоненциального роста, характерный для положительной обратной связи, и участок асимптотического роста, характерный для отрицательной обратной связи. Типичным примером S-образной кривой является рост численности популяции на замкнутой территории или рост производительности однотипного оборудования по мере его амортизации. Такое поведение системы означает, что в ней сначала действует положительная обратная связь, а затем отрицательная. Диаграмма потока и уровня для простейшей системы с S-образным ростом приведена на рис. 7.11.

Такого рода поведение обеспечивается специальным способом определения темпа. Величина темпа задается таблично в виде функции RTV, зависящей от значения уровня LEV. На начальном участке темп нарастает, а затем уменьшается.
Моделирование запаздывания
В реальных системах всегда имеется запаздывание, связанное с тем, что принимаемое решение реализоваться мгновенно не может, так как все процессы в природе инерционны. Смысл запаздывания состоит в том, что любой входящий поток появляется на выходе не сразу, а через некоторое время. Типичные случаи запаздывания показаны на рис. 7.12. Для учета запаздывания в модели системной динамики вводятся специальные элементы запаздывания.

Запаздывание реализуется путем перетекания потока через ряд промежуточных резервуаров. Пример реализации блока запаздывания приведен на рис. 7.13.

Построение модели
Весь процесс построения модели системной динамики можно разбить на ряд этапов.
|
|
|
1. Анализ вербального описания моделируемой системы с целью выделения отдельных элементов и выяснения способов их взаимодействия.
. Построение диаграммы причинно-следственных связей, определение полярностей связей и контуров причинно-следственных связей.
3. Выделение среди переменных уровней и потоков.
. Построение на основе диаграммы причинно-следственных связей диаграммы потоков и уровней.
. Перевод диаграммы потоков и уровней в математическую форму, т.е. написание уравнений динамики модели.
Задавая различные варианты поведения модели, меняя ее уравнения и структуру, можно изучать поведение моделируемого объекта и находить управленческие решения, приводящие объект в желаемое состояние.
Модели мировой динамики
В этом пункте мы рассмотрим модели мировой динамики, предложенные Дж. Форрестером и Д. Медоузом. В основе этих моделей лежит рассмотренный выше метод системной динамики.
При создании простой модели мира специалистов в области управления интересовали лишь наиболее общие режимы поведения во времени системы «население - капитал». Под термином «режимы поведения» понимаются основные тенденции изменения во времени переменных системы (например, численности населения или величины загрязнения окружающей среды).
В модели Форрестера проводится анализ пяти основных тенденций мирового развития:
- ускоряющаяся индустриализация;
- быстрый рост населения;
- необеспеченность продуктами питания;
- истощение невозобновимых ресурсов;
- ухудшение состояния окружающей среды.
Пользуясь своим методом, Форрестер разработал модель МИР-2, где описал мир в целом. В качестве основных элементов мира рассматривались: население; капиталовложения (фонды); природные ресурсы; часть фондов, вкладываемая в сельское хозяйство; загрязнение (уровень загрязнения). Параметры модели оценивались с помощью статистики в интервале с 1900 по 1970 год, прогнозные расчеты велись для интервала с 1970 до 2100 года.
Расчеты показали, что при инерционном развитии в результате ухудшения условий жизни численность населения снизится примерно с 6 млрд человек в 2030 году до 1 млрд в 2065 году. Условия жизни и численность населения стабилизируются, если в 1970 году уменьшатся следующие показатели: темп использования природных ресурсов на 75%, образование загрязнений на 50%, инвестиции на 40%, производство продовольствия на 20%, темп рождаемости на 30%.
|
|
|
Каждый из пяти уровней является основной переменной в основных подсистемах мировой модели. Пять уровней по-разному взаимодействуют друг с другом. Каждый уровень увеличивается или уменьшается в зависимости от связанных с ним темпов. Во всех системах уровни изменяются только вследствие темпов потока, а темпы зависят только от системных уровней с помощью схемы информационных связей. Системная структура состоит только из уровней и темпов.
Д. Медоуз и его коллеги предложили «стандартный компьютерный расчет модели мира». Они выдвинули предположение о том, что в будущем не произойдет великих перемен ни в системе общечеловеческих ценностей, ни в механизме функционирования глобальной системы «население - капитал» (этот механизм уже работает на протяжении ста последних лет). С помощью компьютера были построены графики изменения во времени восьми величин:
- суммарной численности населения;
- выпуска промышленной продукции на душу населения (долларовый эквивалент на человека в год);
- производства продуктов питания на душу населения (килограмм зернового эквивалента на человека в год);
- загрязнения окружающей среды (множитель к уровню 1970 года);
- невозобновимых ресурсов (доля оставшихся ресурсов в сравнении с резервными запасами на 1900 год);
- общего темпа рождаемости (количество рождений на 1000 человек в год);
- общего темпа смертности (количество смертей на 1000 человек в год);
- производства услуг на душу населения (долларовый эквивалент на человека в год).
Начальные значения всех уровней модели (население, капитал, загрязнение окружающей среды, и т.п.) задаются равными их значениям в 1900 году. Были получены следующие результаты.
Значения основных переменных с 1900 по 1970 год в основном согласуются с их историческими значениями в той степени, в какой эти исторические значения нам известны. Население возрастает с 1,6 млрд человек в 1900 году до 3,5 млрд к 1970 году. Хотя темп рождаемости постепенно снижается, темп смертности снижается более быстро, в особенности после 1940 года, и в итоге общий темп роста численности населения возрастает. Выпуск промышленной продукции, производство продуктов питания и услуг на душу населения растут экспоненциально. В 1970 году ресурсная база все еще составляет около 95 % в сравнении со значением на 1900 год, но после этого она катастрофически уменьшается, в то время как численность населения и выпуск промышленной продукции продолжают расти.
|
|
|
Имитационный эксперимент с полной очевидностью показал неизбежность наступления глобального кризиса. Причиной наступления краха является истощение невозобновимых природных ресурсов. Запасы промышленного капитала возрастают до такого уровня, что для его эксплуатации требуются колоссальные затраты ресурсов. Именно этот процесс роста капитала приводит к расходованию большой доли доступных запасов ресурсов. Когда цены на ресурсы начинают расти, а их месторождения истощаться, становится необходимым использование всевозрастающих объемов капитала в ресурсных отраслях, в результате чего уменьшается доля, идущая на инвестирование и обеспечение роста в других отраслях. Наконец, это инвестирование становится настолько малым, что уже не может покрывать даже амортизацию капитала, и наступает крах промышленной производственной базы. Он тянет за собой системы производства услуг и сельского хозяйства, которые стали зависимыми от производимых для них промышленностью факторов обеспечения производства (таких, как удобрения, пестициды, клинические лаборатории, компьютеры и, особенно, энергоносители для механизированного оборудования). В течение короткого промежутка времени ситуация остается особенно серьезной из-за того, что население продолжает расти вследствие наличия запаздываний, определяемых его возрастной структурой и длительностью процессов социальной адаптации. В конце концов численность населения снижается, когда темп смертности вырастает из-за недостатка продуктов питания и медицинских услуг. Точное время наступления этих событий не является значимым при данном высоком уровне агрегирования и большом количестве неопределенностей в модели.
Заключение
Анализируя системно-динамический подход в целом, необходимо отметить следующие аспекты прогнозирования.
1. Все сценарии прогноза нужно воспринимать прежде всего с качественной стороны, что само но себе уже крайне важно.
|
|
|
2. Прогнозы на длительные сроки заведомо неустойчивы, поскольку они представляют собой экстраполирование современных экономических и технологических возможностей на далекое будущее.
3. Как известно, мультипликатор научно-технического прогресса является экспоненциально растущим во времени. В силу этого цикл смены технологий сильно сокращается: если раньше от составлял десятки лет, то теперь высокие технологии обновляются всего за несколько лет. Следовательно, мы сейчас стоим па пороге разработки и внедрения принципиально новых ресурсосберегающих, ресурсозаменяющих и замкнутых технологий производства. Разумеется, процесс использования таких технологий будет далеко не равномерным по разным странам и регионам.
4. По-видимому, в ближайшем будущем имеет смысл проводить прогноз с использованием системно-динамических моделей с обновленными программными модулями отражающими новые технологии, причем в силу возрастающей интенсивности темпов развития этих технологий вряд ли имеет смысл прогнозирование на период более 50 лет.
5. Ввиду активизации процессов глобализации мировой экономики следует уделять большее внимание аспекту координированного управления экономическими процессами и техногенным влиянием человека на биосферу и окружающую среду с целью выбора оптимальных стратегий эволюции эколого-экономических систем.
модель мировая динамика
Используемая литература
1. Форрестер Дж. Мировая динамика. М.: Наука, 1978.
2. М.С. Красс, Б.П. Чупрынов Математические методы и модели для магистрантов экономики.
.Горстко А.Б., Угольницкий Г.А. Введение в моделирование эколого-экономических систем. Ростов н/Д.: Изд-во Ростов. ун-та, 1990.
|
|
|


