 |
Пример решения задачи линейного программирования симплексным методом
|
|
|
|
Задания к выполнению лабораторной работы
Специальность 080502 Экономика и управление на предприятии (в аграрном производстве)
080801 Прикладная информатика в экономике
Уфа 2006
УДК 519.8
ББК 22.18
Л 12
Рекомендовано к изданию методической комиссией экономического факультета (протокол № 7 от «__29_» мая 2006 г.)
Составитель: ст. преподаватель Сагадеева Э. Ф.
Рецензент: к.т.н., доцент кафедры информатики и информационных технологий Т. Г. Дидык
Ответственный за выпуск: заведующий кафедрой статистики и информационных систем в экономике д.э.н., профессор Рафикова Н.Т.
ОГЛАВЛЕНИЕ
| Введение | |
| 1. Алгоритм симплексного метода | |
| 2. Пример решения задачи линейного программирования симплексным методом | |
| 3. Задачи для самостоятельного решения | |
| Библиографический список | |
Введение
Решение любой ЗЛП можно найти либо симплекс методом, либо симплекс методом с искусственным базисом.
Симплекс метод – это вычислительная процедура, основанная на принципе последовательного улучшения решения.
Симплекс метод позволяет, исходя из известного опорного плана задачи, за конечное число шагов получить ее оптимальное решение.
Каждый из шагов (итераций) состоит в нахождении нового плана, которому соответствует лучшее, или, по крайней мере, не худшее значение целевой функции (по сравнению с предыдущим планом).
Доказано, что если оптимальное решение существует, то оно будет найдено через конечное число шагов.
Если задача не имеет решения или линейная функция не ограничена, симплекс метод позволяет установить это в процессе вычисления.
|
|
|
В отличие от графического метода, симплекс метод позволяет решать задачи не с двумя, а с п переменными.
Симплексный метод - это вычислительная процедура, основанная на принципе последовательного улучшения решений при переходе от одной базисной точки (базисного решения) к другой. При этом значение целевой функции улучшается.
Базисным решением является одно из допустимых решений, находящихся в вершинах области допустимых значений. Проверяя на оптимальность вершину за вершиной симплекса, приходят к искомому оптимуму. На этом принципе основан симплекс-метод.
Симплекс - это выпуклый многоугольник в n-мерном пространстве с n+1 вершинами, не лежащими в одной гиперплоскости (гиперплоскость делит пространство на два полупространства).
Например, линия бюджетных ограничений делит блага на доступные и недоступные.
Доказано, что если оптимальное решение существует, то оно обязательно будет найдено через конечное число итераций (шагов), кроме случаев «зацикливания».
1 Алгоритм симплексного метода.
Алгоритм симплексного метода состоит из ряда этапов
Первый этап. Строится исходная ОМ. Далее исходная матрица условий преобразуется в приведенную каноническую форму, которая среди всех других канонических форм выделяется тем, что:
а) правые части условий (свободные члены bi) являются величинами неотрицательными;
б) сами условия являются равенствами;
в) матрица условий содержит полную единичную подматрицу.
Если свободные члены отрицательные, то обе части неравенства умножаются на -1, а знак неравенства меняется на противоположный. Для преобразования неравенств в равенства вводятся дополнительные переменные, которые, обычно, обозначают объем недоиспользованных ресурсов. В этом их экономический смысл.
|
|
|
Наконец, если после добавления дополнительных переменных, матрица условий не содержит полную единичную подматрицу, то вводятся искусственные переменные, которые не имеют никакого экономического смысла. Они вводятся исключительно для того, чтобы получить единичную подматрицу и начать процесс решения задачи при помощи симплексного метода.
В оптимальном решении задачи все искусственные переменные (ИП) должны быть равными нулю. Для этого вводят ИП в целевую функцию задачи с большими отрицательными коэффициентами (-М) при решении задачи на max, и с большими положительными коэффициентами (+М), когда задача решается на min. В этом случае даже незначительное ненулевое значение ИП будет резко уменьшать (увеличивать) значение целевой функции. Обычно М в 1000 раз должно быть больше, чем значения коэффициентов при основных переменных.
Второй этап. Строится исходная симплекс-таблица и отыскивается некоторое начальное базисное решение. Множество переменных, образующих единичную подматрицу, принимается за начальное базисное решение. Значения этих переменных равны свободным членам. Все остальные внебазисные переменные равны нулю.
Третий этап. Проверка базисного решения на оптимальность осуществляется при помощи специальных оценок коэффициентов целевой функции. Если все оценки коэффициентов целевой функции отрицательны или равны нулю, то имеющееся базисное решение - оптимальное. Если хотя бы одна оценка коэффициента целевой функции больше нуля, то имеющееся базисное решение не является оптимальным и должно быть улучшено.
Четвертый этап. Переход к новому базисному решению. Очевидно, что в оптимальный план должна быть введена такая переменная, которая в наибольшей степени увеличивает целевую функцию. При решении задач на максимум прибыли в оптимальный план вводится продукция, производство которой наиболее выгодно. Это определяется по максимальному положительному значению оценки коэффициента целевой функции.
Столбец симплексной таблицы с этим номером на данной итерации называется генеральным столбцом.
Далее, если хотя бы один элемент генерального столбца аij0 строго положителен, то отыскивается генеральная строка (в противном случае задача не имеет оптимального решения).
|
|
|
Для отыскания генеральной строки все свободные члены (ресурсы) делятся на соответствующие элементы генерального столбца (норма расхода ресурса на единицу изделия). Из полученных результатов выбирается наименьший. Соответствующая ему строка на данной итерации называется генеральной. Она соответствует ресурсу, который лимитирует производство на данной итерации.
Элемент симплексной таблицы, находящийся на пересечении генеральных столбца и строки, называется генеральным элементом.
Затем все элементы генеральной строки (включая свободный член), делятся на генеральный элемент. В результате этой операции генеральный элемент становится равным единице. Далее необходимо, чтобы все другие элементы генерального столбца стали бы равны нулю, т.е. генеральный столбец должен стать единичным. Все строки (кроме генеральной) преобразуются следующим образом. Полученные элементы новой строки умножаются на соответствующий элемент генерального столбца и полученное произведение вычитается из элементов старой строки.
Значения новых базисных переменных получим в соответствующих ячейках столбца свободных членов.
Пятый этап. Полученное базисное решение проверяется на оптимальность (см. третий этап). Если оно оптимально, то вычисления прекращаются. В противном случае необходимо найти новое базисное решение (четвертый этап) и т. д.
Пример решения задачи линейного программирования симплексным методом
Пусть необходимо найти оптимальный план производства двух видов продукции (х1 и х2).
Исходные данные:
| Вид продукции | Норма расхода ресурса на единицу прибыли | Прибыль на единицу изделия | |
| А | В | ||
| Объем ресурса |
1. Построим экономико-математическую модель
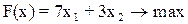
 - ограничение по ресурсу А;
- ограничение по ресурсу А;
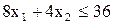 - ограничение по ресурсу В.
- ограничение по ресурсу В.
2. Приведем задачу к приведенной канонической форме. Для этого достаточно ввести дополнительные переменные Х3 и Х4. В результате неравенства преобразуются в строгие равенства.
|
|
|

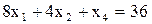
Построим исходную симплексную таблицу и найдем начальное базисное решение. Им будут дополнительные переменные, т. к. им соответствует единичная подматрица.
x3 =20 и x4 =36
| Базисные переменные | Свободные члены (план) | x1 | x2 | x3 | x4 |
| x3 | |||||
| x4 | |||||
| Fj - Cj |
1- я итерация. Находим генеральный столбец и генеральную строку
max (7,3) = 7
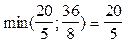
Генеральный элемент равняется 5.
| Базисные переменные | Свободные члены (план) | x1 | x2 | x3 | x4 |
| x1 | 0.4 | 0.2 | |||
| x4 | 0.8 | -1.6 | |||
| Fj - Cj | 0.2 | -1.4 |
2-я итерация. Найденное базисное решение не является оптимальным, т. к. cтрока оценок (Fj-Cj) содержит один положительный элемент. Находим генеральный столбец и генеральную строку:
max (0,0.3,-1.4,0) = 0.2
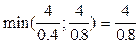
| Базисные переменные | Свободные члены (план) | x1 | x2 | x3 | x4 |
| x1 | -0.5 | ||||
| x2 | -2 | 1.25 | |||
| Fj - Cj | -1 | -0.25 |
Найденное решение оптимально, так как все специальные оценки целевой функции Fj - Cj равны нулю или отрицательны. F(x)=29 x1 =2; x2 =5.
|
|
|


