 |
Реакции нулевого, первого, второго и третьего порядков.
|
|
|
|
Реакция нулевого порядка.
Для реакции нулевого порядка по реагенту кинетическое уравнение имеет вид:

В результате интегрирования получаем зависимость концентрации от времени:

CA0 - начальная концентрация вещества А,
CA – концентрация вещества А через время τ,
k0 – константа скорости реакции нулевого порядка, [моль/л·сек]
τ – время, сек.
Кинетическая кривая реакции нулевого порядка:
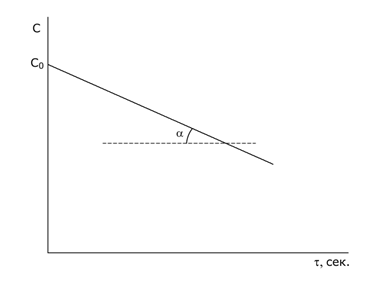
tg α = k
Время, необходимое для достижения концентрации CA:

Важной кинетической характеристикой является период полупревращения, т.е. время, в течение которого вступит в реакцию половина первоначально взятого вещества, СA=0,5CA0

Реакция первого порядка.
Для реакции 1-го порядка A → B по реагенту кинетическое уравнение имеет вид:
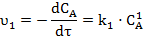
Разделим переменные и проинтегрируем:


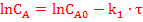

Кинетическая кривая реакций 1-го порядка:


!!! Зависимость концентрации от времени:

!!! Константа скорости реакции первого порядка:

!!! Период полупревращения СA=0,5CA0 не зависит от начальной концентрации:

Реакция второго порядка.
Большинство реакций являются реакциями второго порядка.
A + B → продукты или 2А ® продукты.
Кинетическое уравнение реакции второго порядка:

Пусть CA0 = CB0

Разделим переменные и проинтегрируем:


!!! Константа скорости реакции второго порядка:

!!! Кинетическая кривая реакций 2-ого порядка:
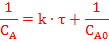

tgα = k2
!!! Период полупревращения СA=0,5CA0 реакции второго порядка:


Период полупревращения обратно пропорционален начальной концентрации.
Реакции третьего порядка.
A + B + C → продукты
Скорость реакции третьего порядка:
|
|
|

Если начальные концентрации равны, CA0 = CB0= CС0

Разделим переменные и проинтегрируем:



!!! Константа скорости реакции третьего порядка:

!!! Период полупревращения:

Приведенные кинетические уравнения – только первоначальный этап исследования. При дальнейшем исследовании какой-либо реакции, ее механизм будет уточняться и уточнения ее стадий, кинетический уравнения и форма кинетических кривых могут значительно изменяться.
5. Скорость обратимых реакций.
Обратимые реакции протекают в прямом и обратном направлении, поэтому скорость реакции равна разности прямой и обратной реакций.
A + B ↔ AB

 – скорости прямой и обратной реакции,
– скорости прямой и обратной реакции,
 – константы скорости прямой и обратной реакции.
– константы скорости прямой и обратной реакции.
По мере протекания реакции концентрации исходных веществ уменьшаются, а продуктов растут. При некоторой концентрации исходных веществ скорости прямой и обратной реакции становятся равными:



Выражение закона действующих масс:

Для обратимых химических реакции необходимо учитывать скорости прямых и обратных реакций. Константа химического равновесия равна отношению констант скоростей прямой и обратной реакции.
6. Зависимость скорости реакции от температуры. Энергия активации.
Температура характеризует среднюю кинетическую энергию хаотического движения молекул. Отсюда очевидно, что с ростом температуры должна увеличиваться скорость любой химической реакции. Вант-Гофф на основании экспериментальных данных установил правило: в условиях не слишком высоких и низких температур скорость большинства химических реакций увеличивается в 2…4 раза при повышении температуры на 100С:

υ2 и υ1 – скорости реакции при температурах T2 и Т1, γ – температурный коэффициент, показывающий во сколько раз возрастает скорость при увеличении температуры на 100С. Температурный коэффициент эндотермической реакции всегда выше температурного коэффициента экзотермической реакции. Правило Вант Гоффа применимо только для ориентировочных расчетов.
|
|
|
Более точно зависимость скорости химической реакции от температуры отражает уравнение Аррениуса (1889 г.), которое описывает влияние температуры на константу скорости химической реакции k:

k – константа скорости реакции,
k0 – предэкспоненциальный множитель, по физическому смыслу он отражает число столкновений частиц в реакционной смеси,
EA – экспериментальная энергия активации. Она представляет собой избыток энергии, который необходимо иметь частице (молекуле) для того, чтобы при данных условиях вступить в реакцию. Это избыток по отношению к средней энергии частиц при данной температуре. Энергия активации выражается в энергетических единицах, отнесенных к одному молю реагирующих частиц и имеет размерность [кДж/моль]. Значение энергии активации для химических реакциях лежит в пределах 40-400 кДж/моль.
Энергия активации не является функцией температуры. Источником активации может служить тепловая, световая, электрическая энергия, радиоизлучение и т.д.
По распределению Максвелла-Больцмана: число активных молекул

если Т = 300К, Еа = 100483 Дж/моль

То есть из 1018 молекул - только 4 активные.
Для определения экспериментальной энергии активации, необходимо записать уравнение зависимости константы скорости химической реакции от энергии активации в следующем виде:


Далее по экспериментальным точкам строят график:

Прямая отсекает на оси ординат отрезок, равный lgk0, угол α связан с энергией активации выражением:

При этом нужно помнить, что ЕА величина размерная, поэтому для расчета tgα нужно брать не геометрические отрезки, а их размерные значения.
Уравнение Аррениуса в дифференциальной форме:

Поскольку Ea/RT2>0, с ростом температуры увеличивается константа скорости химической реакции.!!!! Зная значения констант скорости при температурах T1 и Т2, можно рассчитать Ea:

7. Активированный комплекс. Энергетическая диаграмма реакции.
С современной точки зрения элементарный акт химической реакции протекает как непрерывный последовательный процесс сближения молекул реагентов, образования из них на определенном этапе сложной промежуточной частицы – активированного комплекса – и последующего распада активированного комплекса на продукты реакции. Реакция AB + CD → AC + BD с точки зрения теории активированного комплекса выглядит следующим образом:
|
|
|

В активированном комплексе старые связи еще не разорвались, но ослаблены, новые связи только формируются. Время существования активированного комплекса порядка
10-14-10-11 секунд. При распаде активированного комплекса либо образуются исходные вещества, либо продукты реакции. Активированный комплекс является тем объектом, в котором кинетическая энергия частиц реагентов переходит сначала в потенциальную энергию комплекса, а потом – в химическую энергию новой конфигурации частиц и их кинетическую энергию движения.
Энергия, необходимая для перехода вещества в состояние активированного комплекса называется энергией активации. Молекула, энергии которой достаточно для образования активированного комплекса называется активной. Скорость реакции определяется числом столкновений, в которых принимают участие активные молекулы, кинетическая энергия которых выше предела, называемого энергией активации.
Система в состоянии активированного комплекса имеет более высокую энергию, чем в исходном и конечном состоянии.

Для реакции AB + CD ↔ AC + BD
Прямая реакция:


Обратная реакция
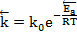

Вычитая из первого уравнения второе, получаем:

К – константа равновесия по закону действующих масс.
Выражение изобары Вант Гоффа:

Отсюда связь кинетических и термодинамических параметров: 
Константа скорости эндотермической реакции с ростом температуры возрастает быстрее, чем константа скорости экзотермической реакции.
Высокое значение энергии активации является причиной того, что многие химические реакции при невысоких температурах не протекают, хотя принципиально возможны с точки зрения термодинамики (ΔrG<0).
|
|
|
8. Катализ.
Применение катализаторов является одним из наиболее эффективных способов ускорения химических реакций.
Катализ – это явление изменения скорости химической реакции, вызванное особым механизмом ее протекания и обусловленное присутствием в зоне реакции катализаторов.
Катализаторы – это химические агенты, изменяющие скорость протекания химических реакций за счет включения в периодически повторяющийся цикл химических превращений, приводящих к возникновению продуктов реакции и восстановлению активного состояния катализатора.
Обычно под катализом понимают именно ускорение химической реакции. Если химический агент замедляет реакцию, используют термин ингибирование, а агент называют ингибитором.
Катализатор не влияет на термодинамику химической реакции, т.е. не изменяют энтальпию и энергию Гиббса. Если ΔrG>0, то в присутствии катализатора процесс не станет самопроизвольным. Катализатор увеличивает константу скорости химической реакции. Катализатор не изменяет значение константы равновесия, но укоряет достижение этого состояния. Катализатор увеличивает константу скорости прямой и обратной реакции.
Каталитическая активность, т.е. способность ускорять реакцию, для многих катализаторов возрастает с добавлением некоторых веществ, называемых промоторами. С другой стороны, есть вещества, снижающие каталитическую активность, их называют каталитическими ядами.
Катализатор не влияет на начальное и конечное состояние системы, он изменяет механизм реакции, участвуя в образовании иного активированного комплекса. В настоящее время признано, что катализатор уменьшает полную энергию активации процесса.
Реакция без катализатора: A + B ↔ A···B → AB
В присутствии катализатора: A + B + K ↔ A···B···K → AB + K

В некоторых случаях каталитическая реакция может протекать через образование нескольких активированных комплексов. Но суммарная энергия активации все равно будет ниже, чем процесса без катализатора.
Рассмотрим в общем виде реакцию AB + D → A···B···D → A + BD
Та же реакция в присутствии катализатора будет происходить по другим стадиям:
B + K ↔ D···K ↔ DK
DK + AB ↔ A···B···D···K → A + BD + K

Увеличение константы скорости каталитического процесса kкат по отношению к процессу без катализатора k составляет:

Это отношение часто используют в качестве меры каталитической активности.
Различают гомогенный и гетерогенный катализ.
Гомогенный катализатор находится в том же фазовом состоянии, что и реагенты.
Если катализаторы и реагенты находятся в разных фазах и имеют границу раздела, то катализ называется гетерогенным. Суммарная скорость химического превращения на гетерогенном катализаторе зависит от площади его поверхности, поэтому обычно применяют катализаторы с развитой поверхностью, либо катализаторы, нанесенные на поверхность носителя с развитой поверхностью.
|
|
|
Проведение каталитической реакции в гетерогенной среде значительно усложняет условия протекания процесса из-за влияния на его ход диффузионных и адсорбционно-десорбционных стадий. Перед тем, как произойдет образование активированного комплекса одного из реагентов с катализатором, это реагент должен быть «доставлен» к поверхности раздела фаз, на которой расположены активные центры катализатора. Затем происходит адсорбция реагента на активных центрах, происходит химическая реакция и десорбция продуктов реакции. Если какая-либо примесь сорбируется на катализаторе необратимо, происходит блокирование активных центров катализатора. Это приводит к снижению скорости основной реакции, т.н. отравление катализатора. Например, каталитическими ядами платиновых катализаторов являются соединения серы, мышьяка, ртути, монооксид углерода.
Катализ является очень сложным комплексом процессов химической и физико-химической природы. Это не позволило до настоящего момента построить общую теорию катализа и удовлетворительно предсказывать каталитические свойства веществ.
Задача.
Во сколько раз изменится скорость элементарной реакции:
2СО(г) + О2(г) ® 2СО2(г)
при увеличении давления в системе в 10 раз? Температура системы поддерживается постоянной.
Решение.
Для элементарной реакции справедлив закон действующих масс:
υ = k×с2(СО)×с(О2).
Учитывая, что концентрация и парциальное давление связаны прямо пропорциональной зависимостью
рi = сi×RT,
получим, что
υ = k×р2(СО)×р(О2).
После увеличения давления в системе в 10 раз парциальное давление каждого из реагентов возрастет тоже в 10 раз, т. е.
υ'= k×(10р(СО))2×10р(О2) = 1000 k×р2(СО)×р(О2) = 1000 υ
Cкорость реакции увеличится в 1000 раз.
Задача.
В реакции А ® В + С с общим порядком, равным единице, константа скорости k 1 = 5×10-5 с-1. Определите концентрацию веществ А и В и скорость реакции через 1 час и через 5 часов, если начальная концентрация А составляла 0,2 моль/л.
Решение.
Для реакции 1-го порядка справедливо уравнение

с – текущая концентрация вещества в момент времени τ,
с0 – начальная концентрация,
k – константа скорости,
τ – время.
Через 1 час:

Через 5 часов:

Концентрация вещества В находится по стехиометрическому соотношению веществ А и В. Из уравнения реакции следует, что концентрация вещества В возрастает на ту же величину, на какую убывает концентрация А, т. к. из 1 моль А получается 1 моль В.
Через час: 
Через 5 часов: 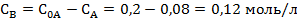
Скорость реакции рассчитывают по уравнению:

Через час: υ = 5·10-5·0,17 = 8,5·10-6 моль/(л·сек)
Через 5 часов: υ = 5·10-5·0,08 = 4,6·10-6 моль/(л·сек)
Задача.
Для реакции первого порядка А ® 2В определите время, за которое прореагирует 90 % вещества А. Константа скорости реакции k1 = 10-4 с-1.
Решение.
После превращения 90 % вещества А его концентрация составит 10% от начальной концентрации, т. е. 0,1 с0.
Из уравнения  получим, что
получим, что  , следовательно
, следовательно
τ = ln10/k1 = 23026 с = 6,4 ч
Задача.
При изучении кинетики термического разложения ацетона, являющегося реакцией первого порядка, в соответствии с уравнением:
СН3СОСН3(г) ® С2Н4(г) + СО(г) + Н2(г)
получены следующие экспериментальные данные при Т = 802 К: давление в реакторе изменилось от начального р0 = 312 мм. рт. ст. до 408 мм. рт. ст. за 390 с. Рассчитайте константу скорости реакции.
Решение.
Все вещества в системе находятся в газообразном состоянии, и, учитывая условия проведения опыта, предполагаем, что они подчиняются законам идеальных газов. Следовательно, концентрация и парциальное давление газа связаны зависимостью
pi = ci×R×T или 
Отсюда, для реакции I-го порядка:
 и
и 
Если р0 – это начальное давление ацетона в реакционном сосуде, то для решения задачи необходимо определить парциальное давление этого вещества к моменту времени, когда общее давление  составило 408 мм. рт. ст.
составило 408 мм. рт. ст.
Из стехиометрии реакции видно, что 1 моль ацетона, распадаясь, образует 3 моль газа. Из закона Авогадро следует, что при уменьшении парциального давления ацетона на Dр сумма парциальных давлений образовавшихся газов составит 3Dр. Таким образом, можно записать^
P = p0 – Dp + 3×Dp
или
408 = 312 + 2×Dp, Dp = 48 мм рт.ст.
Следовательно, парциальное давление ацетона через 390 с после начала опыта составило 312 – 48 = 264 (мм. рт. ст.).
После подстановки в уравнение:
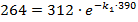
k1 = 4,28·10-4 сек-1
Задача.
При температуре 100°С константа скорости реакции второго порядка
2НI(г) ® Н2(г) + I2(г)
равна 8,83×10-16 л/(моль×с). Определите время полупревращения йодистого водорода, если начальная концентрация его равна 1 моль/л.
Решение.
Уравнение для реакции второго порядка:

Задача.
Рассчитайте изменение константы скорости реакции, имеющей энергию активации 191 кДж/моль, при увеличении температуры от 330 до 400 К.
Решение.
Зависимость константы скорости реакции от температуры определяется уравнением Аррениуса:
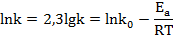
Логарифм отношения констант скоростей реакции при температурах Т2 и Т1 соответственно равен:

где R = 8,31 Дж/(моль×К) – универсальная газовая постоянная.
Подставив в это уравнение данные задачи:


Задача.
При исследовании кинетики реакции распада диметилового эфира были получены следующие данные:
| Время τ, сек | ¥ | ||||
| Повышение давления, Па (Dр×10-4) | 1,28 | 2,35 | 3,33 | 6,23 | 8,25 |
Начальное давление диметилового эфира 4,16×104 Па. Рассчитайте порядок реакции и константу скорости распада диметилового эфира.
Решение.
Предположим, что реакция имеет первый порядок:

Вместо концентраций используем давления, тогда:

Подставляя соответствующие значения изменения давления со временем в полученное уравнение, рассчитаем константу скорости:




Константа скорости постоянна в пределах погрешности эксперимента, следовательно, предположение, что реакция является реакцией I-го порядка, верно.
Отсюда k ср = 4,36×10-4 с-1.
Задача.
В элементарной реакции А + В ® D за 45 минут концентрации веществ А и В уменьшились на 20%. Начальные концентрации с0А=с0В=0,3 моль/л. Определите константу скорости реакции и период полупревращения.
Задача.
При добавлении катализатора энергия активации реакции при 802 К уменьшилась на 20 кДж. Как и во сколько раз изменилась скорость реакции?
|
|
|


