 |
Методические указания к выполнению лабораторной работы № 1
|
|
|
|
1. Перед выполнением работы ознакомиться с основными определениями и формулами из раздела «Теоретическая часть».
2. Ознакомиться с заданием к лабораторной работе и выполнить п. 1 задания, принимая во внимание, что при последовательном соединении звеньев передаточная функция САУ равна произведению их передаточных функций:
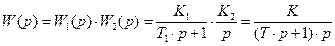, где К = К 1∙ К 2, Т = Т 1.
3. Перед выполнением пункта 2 задания ознакомиться в Приложении с краткими сведениями по использованию базовой программы MATLAB, после чего запустить программу MATLAB и выполнить следующую последовательность действий:
1) задать в окне команд описание передаточной функции САУ W (p) с помощью функции tf (transfer function), параметрами которой являются вектора численных значений коэффициентов числителя и знаменателя передаточной функции. Например, описание передаточной функции W (p) = 10 / (2 ∙ p 2 + 0,5∙ p) будет выглядеть следующим образом: >> sys = tf ([10], [2 0.5 0]).
При нажатии клавиши Enter на экране монитора в окне команд высветится заданная передаточная функция в виде
,
где s – обозначение оператора Лапласа, принятое в МАТЛАБ.
Временную характеристику САУ g (t) строим с помощью функции impulse:
>> impulse (sys); grid,
где grid – признак отображения сетки графика.
При нажатии клавиши Enter на экране монитора в отдельном окне высветится график искомой весовой функции g (t) в виде, представленном на рис. 1.
Рис. 1 График весовой функции g (t) системы САУ,
описываемой передаточной функцией 
Скопировать с экрана график g (t), предварительно свернув все остальные открытые окна, и сохранить его как документ Word в папке «Мои документы» под произвольным именем.
Временная характеристика h (t) САУ строится с помощью функции step:
|
|
|
>> step (sys); grid.
После нажатия клавиши Enter на экране монитора в отдельном окне высветится график искомой переходной функции h (t) в виде, представленном на рис. 2.
Рис. 2 График переходной функции h (t) системы САУ,
описываемой передаточной функцией
Аналогичным образом скопировать с экрана график h (t), предварительно свернув все остальные открытые окна, и вставить его в свой документ Word.
4. Прежде, чем перейти к выполнению пункта 3 задания, необходимо также скопировать с экрана данные окна команд и вставить их в свой документ Word, а затем закрыть программу МАТЛАБ.
5. Выполнить пункты 3 и 4 задания, используя материалы раздела «Теоретическая часть».
6. Оформить отчет, который должен содержать:
- название и цель работы;
- основные определения и расчетные формулы;
- графики зависимостей g (t) и h (t) с отмеченными на них тремя значениями, рассчитанными предварительно по полученным формулам для значений времени t = T 1, 2 T 1 и 3 T 1;
- примерные графики частотных зависимостей с отмеченными на них двумя значениям, рассчитанными предварительно по полученным формулам для значений круговой частоты ω = 0 и 1 / Т 1;
- выводы.
Лабораторная работа № 2
ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ САУ
Цель работы: изучение особенностей практического использования алгебраических и частотных критериев устойчивости для анализа динамики линейных САУ 2-го и 3-го порядков.
Теоретическая часть
САУ называется устойчивой, если с течением времени выходная величина стремится к установившемуся значению при постоянном значении входного сигнала. Линейная САУ называется неустойчивой, если выходная величина неограниченно возрастает с течением времени.
Система САУ будет устойчива, если:
1) все корни pi характеристического уравнения являются действительными отрицательными числами (pi < 0);
2) если имеется пара комплексных и сопряженных корней типа pi,i+1 = α +_ jβ.
|
|
|
Характеристическое уравнение можно получить, приравняв знаменатель передаточной функции САУ, приведенной к стандартному виду, к нулю.
Как правило, на устойчивость и показатели качества исследуются замкнутые системы САУ с коэффициентом обратной связи К ос, равным 1, рис. 3.
Рис. 3 Структурная схема замкнутой САУ
Передаточная функция замкнутой САУ W з имеет следующий вид:
, где W (p) – передаточная функция разомкнутой САУ.
Найдем в качестве примера передаточную функцию замкнутой САУ второго порядка, полученную введением цепи обратной связи в разомкнутую систему с передаточной функцией
W (p) = 
.
W з = 
. (4)
Формулу (4) для передаточной функции W з представим в стандартном виде:
W з = 
, (5)
где 
постоянные времени замкнутой САУ.
Преобразуем выражение (5) к более удобному виду для оценки типа динамического звена, описываемого данным выражением:
W з = 
, (6)
где ξ = 
коэффициент демпфирования, позволяющий определить тип динамического звена второго порядка (при ξ < 1 – колебательное звено, при ξ ≥ 1 – апериодическое звено второго порядка).
Найдем корни характеристического уравнения, приравняв знаменатель передаточной функции (6) нулю:
. (7)
Так как действительная часть корней характеристического уравнения носит отрицательный характер при любых положительных значениях ξ и Т 2з, то можно утверждать, что все линейные САУ второго порядка представляют собой устойчивые системы. Из выражения (7) следует, что при 0 ≤ ξ < 1 характеристическое уравнение динамического звена второго порядка имеет два сопряженных комплексных корня и, соответственно, переходная функция h (t) носит колебательный характер; при ξ ≥ 1 – два отрицательных вещественных корня, что соответствует передаточной функции САУ, состоящей из последовательного соединения двух апериодических звеньев первого порядка с постоянными времени, равными:
. (8)
При исследовании замкнутых САУ более высокого порядка используются алгебраические критерии Рауса, Гурвица или Неймарка, которые с помощью выполнения ряда алгебраических операций над коэффициентами характеристического уравнения позволяют косвенно оценить наличие или отсутствие корней характеристического уравнения, удовлетворяющих условиям устойчивости САУ.
|
|
|
К частотным критериям устойчивости замкнутых систем САУ относятся критерии Найквиста и Михайлова. Оценка устойчивости замкнутых САУ с использованием критериев Найквиста производится на основе анализа АФЧХ или ЛАЧХ (логарифмический критерий Найквиста).
Согласно частотному критерию Найквиста для того, чтобы замкнутая САУ была устойчивой необходимо и достаточно, чтобы годограф ее АФЧХ W (jω) при разомкнутой цепи обратной связи не охватывала в комплексной плоскости точку с координатами (- 1; j0).
Рассмотрим применение частотного критерия Найквиста на примере замкнутой САУ с передаточной функцией W з(р): W з(р) = W (р) / [1 + W (р)], где
W (р) = 
.
При замене переменной р на jω частотная передаточная функция разомкнутой САУ примет вид:
W (jω) = 
=
= 
.
На рис. 4 представлен фрагмент графика функции W (jω) при К = 1, иллюстрирующий момент пересечения годографом АФЧХ действительной отрицательной полуоси. Ввиду того, что точка пересечения приведенного графика с действительной отрицательной полуосью находится правее точки с координатами (-1, j0), то в соответствии с частотным критерием Найквиста при выбранном значении статического коэффициента усиления разомкнутая САУ, будучи охвачена жесткой отрицательной обратной связью, сохранит свою устойчивость.
Рис. 4. Фрагмент графика годографа АФЧХ разомкнутой САУ третьего порядка при К = 1, соответствующий устойчивому состоянию замкнутой САУ
При увеличении коэффициента К точка пересечения годографа функции W (jω) с отрицательной действительной полуосью будет смещаться влево и при превышении граничного значения К гр, соответствующего границе устойчивости САУ, будет находиться левее точки с координатами (-1, j0), как это показано для рассмотренной ранее САУ на рис. 5., но при К = 15. Следовательно, при значении статического коэффициента усиления, равном 15, и охвате разомкнутой САУ жесткой отрицательной обратной связью, полученная замкнутая САУ будет неустойчивой.
|
|
|
Рис. 5 Фрагмент графика годографа АФЧХ разомкнутой САУ третьего порядка при К = 15, показывающий на неустойчивость замкнутой САУ
Полученные выводы, как увидим ниже, полностью подтвердятся и в случае использования логарифмического критерия устойчивости Найквиста.
Логарифмическая амплитудная частотная характеристика (ЛАЧХ) представляет собой зависимость логарифмической функции вида L (ω) = 20 lg [ H (ω)] от круговой частоты. Однако при построении графика ЛАЧХ по оси абсцисс откладывают круговую частоту в логарифмическом масштабе lg (ω), а по оси ординат значение L (ω) в дБ. Так, например, L (ω) = 20 означает, что при прохождении сигнала через звено на данной частоте его амплитуда увеличивается в 10 раз.
ЛФЧХ – это график зависимости частотной функции φ (ω) от десятичного логарифма частоты lg (ω). При его построении по оси абсцисс откладывают частоту в логарифмическом масштабе, по оси ординат откладывают φ (ω) в градусах или радианах.
В обоих случаях за единицу масштаба по оси абсцисс принимается декада – это частотный интервал, соответствующий изменению частоты в 10 раз. Ось ординат при построении этих характеристик проводят часто через точку (ω = 1) которая соответствует началу координат lg (1) = 0.
Для оценки устойчивости САУ по логарифмическому критерию Найквиста используются графики ЛАЧХ и ЛФЧХ разомкнутой системы САУ. Система САУ считается устойчивой, если при φ (ω) = - 180о кривая ЛАЧХ находится в отрицательной области: L (ω) = 20 lg [ H (ω)] < 0. Систему САУ можно считать также устойчивой, если на частоте среза ω ср, при которой справедливо равенство L (ω ср) = 20lg[ H (ω ср)] = 0, значение аргумента φ(ω ср) > - 180o.
При оценке устойчивости САУ необходимо определить запас устойчивости, т.е. степень удаленности системы от границы устойчивости. В качестве меры запаса устойчивости используется запас устойчивости по амплитуде h (ω) и запас устойчивости по фазе ψ(ω ср).
Запас устойчивости САУ по амплитуде h(ω) позволяет оценить критическое значение коэффициента усиления системы, при котором она окажется на грани устойчивости, и определяется на частоте ω у, при которой φ(ωу) = - 180о: h (ω у) = - L (ω у), рис. 6.
Рис. 6 Определение запаса устойчивости САУ по амплитуде и фазе на основе использования логарифмического Критерия Найквиста
Запас устойчивости по фазе ψ(ω ср) определяется на частоте среза ω ср, как: ψ(ω ср) = φ(ω ср) + 180о и показывает, на какую величину должно возрасти запаздывание по фазе в системе на частоте среза ω ср, чтобы система оказалась на грани устойчивости.
|
|
|
|
|
|
