В трехфазной схеме, соединенной звездой

Как вытекает из самого принципа соединения звездой, является очевидным, что линейный ток равен фазному: I_Л = I_Ф. Действительно, как видно из рисунка 5, ток I_A протекает по фазе A генератора, не разветвляясь протекает по линейному проводу A–a и не разветвляясь течет по фазе a приемника.

Ток I_N в нейтральном проводе в соответствии с первым законом Кирхгофа равен сумме фазных (линейных) токов.

В аналитическом методе расчета эта сумма алгебраическая:

(6)

i_N = i_A + i_B + i_C,

где малыми буквами обозначены мгновенные значения токов.

В методе векторных диаграмм эта сумма векторная:

(7)

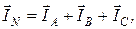
где большими буквами обозначены действующие (средние квадратичные за период) значения токов.

В символическом методе эта сумма алгебраическая [1]:

(8)

где складываются комплексы действующих значений токов .

Рассмотрим, как соотносятся фазные и линейные напряжения применительно к генератору бесконечной мощности, соединенному звездой.

На рисунке 6 показана схема, на которой вольтметр V подключен к началам двух разных фаз А и В. Очевидно падение напряжения на внутренней цепи вольтметра будет представлять собой линейное напряжение U_AB.

Составим, задавшись направлением обхода (рис. 6), уравнение по второму закону Кирхгофа для замкнутого контура, образованного вольтметром V и фазами А и В генератора в векторной форме (метод векторных диаграмм) и перепишем его в виде:

(9)

.

Переключив вольтметр на две другие пары зажимов, получим аналогичные равенства:

(10)

Таким образом, при соединении звездой вектор линейного напряжения равен геометрической разности векторов двух соответствующёих фазных напряжений.

Решим полученные равенства графически с учетом того, что идеальный генератор вырабатывает симметричную систему фазных напряжений, которая может быть представлена симметричной трехлучевой звездой векторов 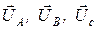(рис. 7).

Рис. 7

Для необходимых графических построений воспользуемся правилом сложения векторов методом многоугольника [1] (в нашем случае методом треугольника), представив записи полученных зависимостей (9) и (10) в виде суммы типа

(11)

.

Рассмотрим подробно (рис. 7) построение вектора (все операции выполняются с соблюдением выбранного масштаба напряжений). Методом параллельного переноса совмещаем начало вектора с концом вектора первого слагаемого . Как известно суммарный вектор получится соединением начала первого слагаемого с концом последнего (в нашем случае второго ).

Проделав аналогичные операции в соответствии с равенствами (10) получаем расположения векторов и (рис. 7). Как видно из рисунка 7 три вектора линейных напряжений , и образуют симметричную трехлучевую звезду векторов, которая опережает звезду фазных напряжений на 30° (с учетом вращения векторов против часовой стрелки).

Чтобы выяснить соотношение между линейным U_Л и фазным U_Ф напряжениями, рассмотрим прямоугольный треугольник D mq0 (рис. 7), который получается, если опустить из вершины тупого угла одного из равнобедренных треугольников высоту (которая является и медианой).

Из D mq0 следуют очевидные равенства: отрезок = 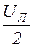; поскольку он является прилегающим к углу 30° катетом, то = 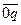cos30°=U_Ф ( =U_Ф).

Приравняв правые части двух равенств, получим:

(12)

U_Л = U_Ф,

то есть линейное напряжение генератора, соединенного звездой, в раз больше фазного ( = 1,73).

Что касается приемника, соединенного звездой, то это соотношение соблюдается только при симметричной нагрузке или при наличии нейтрального (нулевого) провода, если пренебречь его сопротивлением и сопротивлениями линейных проводов.

В дальнейшем будем, как правило, рассматривать трехфазные цепи, считая сопротивления линейных проводов и сопротивление нейтрального провода (если он есть) равными нулю.

С учетом этого предположения можно утверждать, что на приемник, соединенный звездой с нейтральным проводом, передаются от генератора без изменения величины потенциалы начал фаз А, В, С и нейтральные точки N. Таким образом система линейных и фазных напряжений на приемнике при наличии нейтрального провода будет такой же, как и на генераторе, то есть симметричной.

В этом случае электрические потенциалы линейных проводов будут равны потенциалам начал одноименных фаз генератора и приемника, а потенциал нейтрального провода будет иметь потенциал концов всех трех фаз генератора и приемника.

С учетом сказанного является очевидным, что фазное напряжение генератора или приемника можно определить как разность потенциалов между соответствующим линейным проводом и нейтральным проводом, а линейное напряжение как разность потенциалов между двумя линейными проводами.

Отметим, что векторная диаграмма фазных и линейных напряжений генератора, соединенного звездой (рис. 7), может быть представлена в более компактном виде, поскольку векторы линейных напряжений , , одновременно являются сторонами равностороннего треугольника, вершины которого – концы векторов соответствующих фазных напряжений , , (рис. 8).

На рисунке 8 такая диаграмма показана в комплексной плоскости, что позволяет по аналогии с равенствами (9) и (10) получить комплексы линейных напряжений:

(13)

(13)

,

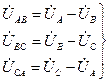где в соответствии с равенствами (2): ; ; .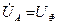

Сделав соответствующие подстановки в (13), получим:

(14)

Нетрудно убедиться, что ввиду симметрии системы линейных напряжений всегда будет справедливо равенство (необходимо сложить правые части равенств (13) или (14)):

(15)

.

1.4. Режимы работы трехфазной цепи при соединении звездой

Будем рассматривать режимы работы трехфазной цепи с нейтральным проводом при условии, что генератор является источником бесконечной мощности, а линейные провода и нейтральный провод не создают потерь напряжения при любой величине токов в них, то есть их полные сопротивления равны нулю (z_л = 0; z_N = 0).

На рисунке 9 показана такая схема с возможностью измерения фазных (линейных) токов, тока в нейтральном проводе амперметрами А и напряжения U_N между нейтральными точками генератора и приемника вольтметром V.

На схеме все электрические величины показаны как комплексные числа. В дальнейшем будем при необходимости считать, что 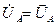, и т.д., поскольку комплексные напряжения и токи – это те же векторы, что и изображающие их комплексные числа. Это позволяет строить векторные диаграммы как в комплексной системе координат, так и без нее.

Рис. 9

Очевидно с учетом принятых допущений режим работы всей цепи будет определяться тем, в каком режиме находится приемник и в каком положении находится ключ К, замыкающий или размыкающий нейтральный провод N – n.

Первый режим, который мы рассмотрим – это режим симметричной нагрузки, когда приемник является симметричным.

Симметричной называется нагрузка, при которой комплексные сопрёотивления фаз приемника равны друг другу:

(16)

z_Ф e ^jj = r_Ф + jx_Ф,

где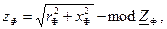

[1]

То есть величины полного (кажущегося) сопротивления каждой фазы приемника z_Ф равны друг другу, а фазные токи будут сдвинуты относительно «своих» фазных напряжений на один и тот же угол φ.

Предположим, что ключ К на схеме (рис. 9) замкнут, то есть со стороны генератора на зажимы приемника a, b, c, n подается симметричная система фазных и линейных напряжений (рис. 8).

Применим закон Ома в комплексной форме [1] для фаз симметричного приемника

= ; = ; = .

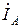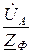Комплекс тока 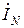в нейтральном проводе согласно первому закону Кирхгофа равен алгебраической сумме комплексов фазных токов

(17)

= + + .

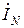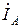Сделав соответствующие подстановки в правую часть равенства (17), получим:

(18)

= ,

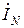то есть ток в нейтральном проводе отсутствует из-за того, что обращается в ноль выражение в скобках (5).

Таким образом при симметричной нагрузке необходимость в нейтральном проводе отпадает, и схема превращается в «трехпроводную звезду» или «звезду без нейтрального провода».

Поэтому заведомо симметричные приемники (например электродвигатели трехфазного тока: асинхронные и синхронные) подключаются к питающей сети только тремя линейными проводами.

В качестве примера на рисунке 10 показана «трехпроводная звезда» с симметричным активно-емкостным приемником. Предположим, что активное и емкостное сопротивления равны друг другу по величине (модулю) r = x_c. Комплексные сопротивления фаз одинаковы и равны , где , .

Рис. 10

Симметричность приемника предполагает равенство нулю тока в нейтральном проводе (), поэтому на схеме (рис. 10) провод N – n не показан.

Рис. 11

На рисунке 11а показана векторная диаграмма фазных напряжений и токов без увязки с системой координат +1, + j комплексной плоскости. Очевидно фазные токи будут одинаковы по величине и опережать «свои» фазные напряжения на угол φ = –45° (как это показано на диаграмме (рис. 11а)). Нетрудно видеть, что три тока 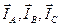образуют симметричную трехлучевую звезду векторов, опережающую на угол φ = –45° звезду векторов фазных напряжений.

Убедимся, что геометрическая сумма векторов фазных токов, показанных в виде трехлучевой симметричной звезды на рисунке 11б, равна нулю, то есть

(19)

.

Решим равенство (19) графически (рис. 11б), используя сложение векторов по правилу многоугольника [1].

В качестве первого слагаемого принимаем вектор . Посредством параллельного переноса второго слагаемого вектора 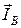(при соблюдении выбранного масштаба) совмещаем его начало с концом первого слагаемого . Проделав аналогичную операцию с третьим слагаемым вектором , убеждаемся, что его конец совпадает с началом первого слагаемого . Поскольку суммарный вектор получается соединением начала первого слагаемого с концом последнего, то суммарный вектор в рассматриваемом случае равен нулю.

Если не соблюдается условие симметричности приемника, то следует предположить появление тока в нейтральном проводе (I_N > 0). Дадим общее определение несимметричной нагрузки.

Несимметричной называется нагрузка, при которой комплексные сопротивления фаз приемника не равны друг другу, то есть .

Следует отметить, что приведенные здесь понятия симметричной и несимметричной нагрузки распространяются и на трехфазные цепи, соединенные треугольником.

Одним из частных случаев несимметричной нагрузки является равномерная нагрузка, при которой по фазам приемника протекают одинаковые по величине токи, но углы сдвига φ между фазными напряжениями и токами отличаются по величине или знаку. Применительно к схеме «звезда с нейтральным проводом» это означает, что модули комплексов сопротивлений фаз равны друг другу: z_a = z_b = z_c = z_Ф, а аргументы – не равны: φ_a ¹ φ_b ¹ φ_c.

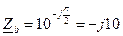Рассмотрим численный пример равномерной нагрузки, когда в схему четырехпроводной звезды (рис. 9) включен приемник с линейным напряжением U_Л = 380В. Фазы приемника имеют одинаковые по величине сопротивления, но различаются по физической природе (рис. 12а): комплексное сопротивление фазы a–x: (резистор); фазы b–y: (идеальный конденсатор); фазы c–z: (идеальная катушка индуктивности).

При наличии нейтрального провода система фазных напряжений приемника симметрична, то есть фазное напряжение на всех фазах одно и то же: . Поскольку модули комплексных сопротивлений всех фаз одинаковы z_a = z_b = z_c = z_Ф =10 Ом, то величина тока во всех фазах одна и та же: .

Рис. 12

В соответствии с первым законом Кирхгофа вектор тока в нейтральном проводе равен геометрической сумме векторов фазных (линейных) токов (17):

.

Решим это равенство графическим методом, построив соответствующую векторную диаграмму (рис. 13).

Рис. 13

Задача облегчается тем, что векторы фазных токов при выбранном масштабе имеют одинаковую длину и сдвинуты относительно своих фазных напряжений на удобные для построения углы: .

В отличие от симметричной нагрузки векторы токов 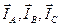вместо симметричной звезды векторов образуют «метелку». Просуммировав векторы в соответствии с равенством (17) по правилу многоугольника, получим суммарный вектор тока в нейтральном проводе, который равен, как в этом нетрудно убедиться с учетом показанных геометрических построений на рисунке 13

.

То есть в приведенном примере ток в нейтральном проводе намного превосходит токи в линейных проводах (фазные токи приемника). Такой случай на практике может встретиться только теоретически.

Рис. 14

Кстати при наличии в фазах приемника реактивных сопротивлений большое значение имеет их взаимное расположение по фазам. Покажем это на рассмотренном выше примере, поменяв местами реактивные сопротивления в фазах b–y и c–z (рис. 12б). На рисунке 14 показана векторная диаграмма фазных токов и напряжений и проведено графическое построение вектора тока в нейтральном проводе в соответствии с равенством

.

Можно показать, что величина этого тока

,

то есть изменение только структуры одного и того же приемника снизило ток в нейтральном проводе в 3,75 раза.

Поскольку при несимметричной нагрузке по нейтральному проводу всегда протекает ток I_N > 0, то можно предположить наличие разности электрических потенциалов между нейтральными точками N генератора и n приемника.

Эта разность потенциалов при разомкнутом нейтральном проводе (ключ K на схеме рис. 9 разомкнут) получила название «напряжение смещения нейтрали», величину которого U_N можно измерить вольтметром V (рис. 9).

Формулу для расчета напряжения U_N можно получить, воспользовавшись методом узловых потенциалов, а точнее методом двух узлов, поскольку схема на рисунке 9 содержит два электрических узла N и n. Вывод такой формулы узлового напряжения для цепей постоянного тока приведен в [2].

Применительно к схеме на рисунке 9 эта зависимость в комплексной форме записи имеет вид:

(20)

где – комплекс напряжения смещения нейтрали;

, , – комплексы фазных напряжений генератора, образующих

симметричную систему векторов (рис. 8);

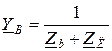; ; – комплексы проводимостей фаз

приемника с учетом комплексных сопротивлений линейных

проводов (если эти сопротивления не равны нулю [7]).

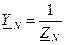– комплексная проводимость нейтрального провода; – его

комплексное сопротивление.

Рассмотрим случай обрыва нейтрального провода (ключ K на схеме рис. 9 разомкнут) при несимметричной нагрузке ( ¹ ¹ 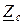) с учетом того, что вольтметр V показывает величину U_N напряжения смещений нейтрали.

Нас будут интересовать фазные напряжения приемника как падения напряжения, создаваемые фазными (линейными) токами на полных сопротивлениях z_a, z_b, z_c фаз (U_Ф = I_Фz_Ф).

Запишем в комплексной форме уравнение по второму закону Кирхгофа для замкнутого контура, образованного фазой A–X генератора, линейным проводом A–a, фазой a–x приемника и цепью вольтметра V между точками N и n (ключ K на схеме рис. 9 разомкнут):

Аналогично для контура B–Y, B–b, b–y, N–n и контура C –Z, C–c, c–z, N–n можно записать:

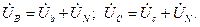
Перепишем полученные равенства в виде

(21)

,

то есть комплексы фазных напряжений приемника получаются алгебраическим вычитанием из комплексов фазных напряжений генератора одной и той же величины: комплекса напряжения смещения нейтрали.

Аналогичные зависимости можно записать и в векторной форме:

(22)

Можно показать, что при вычитании из трех векторов , , , образующих симметричную систему, одного и того же вектора полученные векторы , , будут отличаться друг от друга по величине и не будут сдвинуты по фазе на 120°.

Таким образом при наличии напряжения смещения нейтрали (U_N > 0) работа фаз приемника будет ненормальной, поскольку фазные напряжения будут отличаться от нормальной величины и будут изменяться при изменении режима работы отдельных фаз.

Чтобы восстановить нормальную работу фаз при несимметричной нагрузке необходимо замкнуть ключ K (рис. 9) и восстановить цепь нейтрального провода N–n, сопротивление которого Z _N = 0 . В результате знаменатель в равенстве (20) также стремится к бесконечности, вследствие чего , то есть потенциал нейтральной точки N генератора передается нейтральной точке n приемника.

Поэтому согласно равенствам (21) и (22) фазные напряжения на приемнике , , 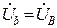, то есть становятся равными соответствующим напряжениям генератора.

На этом основании принято считать, что нейтральный провод обеспечивает независимую работу фаз несимметричного приемника, поскольку фазные напряжения приемника равны друг другу и не зависят от режима работы отдельных фаз.

Следует иметь в виду, что система линейных напряжений на приемнике всегда симметрична вне зависимости от того, есть ли нейтральный провод или он разомкнут. Исключение составляет режим при обрыве линейного провода.

Из равенства (20) можно еще раз убедиться, что при симметричной нагрузке () напряжения смещения нейтрали (поскольку обращается в ноль числитель, и система фазных напряжений приемника будет симметричной как это следует из равенств (21)).

На рисунке 15 приведена векторная диаграмма фазных напряжений генератора и приемника с несимметричной активной нагрузкой во всех фазах (φ_a = φ_b = φ_c = 0, r_a ¹ r_b ¹ r_c) при обрыве нейтрального провода (U_N > 0).

Рис. 15

Из диаграммы видно, что фазные напряжения приемника (они, как и вектор , показаны пунктиром) в соответствии с равенствами (21) и (22) представляют собой несимметричную трехлучевую звезду векторов с центром в точке n. Для рассматриваемого случая фазные напряжения U_a > U_A, U_b < U_B, U_c > U_C. Если в качестве активной нагрузки предположить лампы накаливания, то в фазах a–x и c–z приемника лампы будут быстро перегорать, а в фазе b–y гореть вполнакала.

Как видно из диаграммы (рис. 15) токи I_A, I_B, I_C совпадают по фазе со «своими» фазными напряжениями U_a, U_b, U_c и в сумме дают ноль в соответствии с первым законом Кирхгофа при обрыве нейтрального провода.

Если восстановить цепь нейтрального провода N–n, то напряжение смещения нейтрали U_N = 0; точка n будет совпадать с нейтральной точкой N генератора, и система фазных напряжений на приемнике станет симметричной.

1.5. Соединение фаз генератора и приемника треугольником

На рисунке 16 показана шестипроводная электрически разобщенная трехфазная схема, подготовленная к соединению генератора и приемника треугольником. Все элементы (напряжения, токи и сопротивления) трех однофазных цепей на этой схеме представлены в виде комплексных чисел.

У трехфазных цепей, соединенных треугольником (условное обозначение D) в отличие от соединения звездой (условное обозначение Y) нейтральный провод отсутствует.

Рис. 16

Чтобы получить соединение фазных обмоток генератора треугольником (рис. 16), подключим конец X первой обмотки к началу B второй обмотки, конец Y второй обмотки – к началу C третьей, конец Z третьей – к началу A первой обмотки. Получается замкнутый сам на себя контур (треугольник), в котором действует симметричная система фазных напряжений , , . Никакого дополнительного (уравнительного) тока в контуре при этом не возникает, поскольку сумма фазных э.д.с. (напряжений) равна нулю ( + + = 0), как это было показано раньше (см. раздел 1.1).

Рис. 17

На рисунке 17 показана электрически связанная трехпроводная схема, в которой генератор и приемник соединены треугольником. После объединения фаз генератора и приемника напряжения между концом и началом каждой фазы не изменятся, то есть эти напряжения одинаковы для несвязанной (рис. 16) и связанной (рис. 17) схем. Поэтому не изменятся и токи в фазах приемника 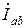, , 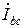в связанной схеме (рис. 17), то есть они будут такими же, как и в несвязанной (рис. 16).

Таким образом из самого принципа соединения в треугольник следует вывод: при соединении треугольником фазное напряжение равно линейному

(23)

U_Л = U_Ф

Это объясняется тем, что потенциал конца предыдущей фазы является также потенциалом начала следующей фазы. Поэтому напряжение между началом и концом фазы (фазное напряжение U_Ф) одновременно является и напряжением между началами двух разных фаз (линейным напряжением U_Л).

Что касается соотношений между линейными и фазными токами, то при замене шести проводов, соединяющих генератор с приемником в несвязанной схеме (рис. 16), тремя линейными проводами A − a, B − b, C − c в связанной схеме (рис. 17), необходимо учитывать наличие электрических узлов A, B, C и a, b, c, в которых распределение токов подчиняется первому закону Кирхгофа [1], [2].

Применив этот закон к соответствующим электрическим узлам приемника или генератора (рис. 17), можно получить следующие соотношения в векторной форме

(24)

Как следует из равенств (24), вектор линейного тока (его действующего значения) равен геометрической разности векторов соответствующих фазных токов, образующих с этим линейным током электрический узел.

Нетрудно видеть из равенств (24), что сумма линейных токов всегда тождественно равна нулю

(25)

.

В данном случае это векторная сумма. В аналитическом и символическом методах расчета эта сумма алгебраическая (соответственно мгновенных значений и комплексов токов) [1].

Равенство нулю суммы линейных токов любой трехпроводной трехфазной схемы можно объяснить с позиций здравого смысла – методом доказательства от противного. Невыполнение этого равенства означает, что в каждый момент времени от генератора (или приемника) течет большее число зарядов, чем обратно. Это означает, что потенциалы на фазах генератора (или приемника) будут возрастать вплоть до бесконечно большой величины, чего на практике не наблюдается.

Несколько замечаний относительно обозначений физических величин в схеме треугольника. В отличие от соединения звездой для фазных токов и напряжений генератора и приемника, а также для сопротивлений фаз приемника применяется двойная индексация, например, U_AB, I_bc, z_ca, что объясняется равенством линейного и фазного напряжения, то есть каждая фаза оказывается подключенной к двум линейным проводам из трех: А–a, В–b, С–c (рис. 17). Что касается токов в линейных проводах, то они, как и при соединении, звездой индексируются одной большой буквой: I_A, I_B, I_C.

1.6. Режимы работы трехфазной цепи при соединении треугольником

Рассмотрим режим симметричной нагрузки. Как и при соединении звездой симметричной называется нагрузка, если комплексные сопротивления фаз приемника равны друг другу, то есть Z _ab = Z _bc = Z _ca = Z _Ф = z_Фe^jφ = r_Ф + jx_Ф, где [1].

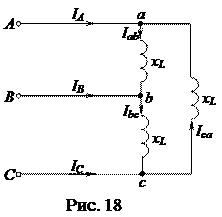
На рисунке 18 показана схема симметричного приемника, соединенного треугольником, в фазы которого включены идеальные катушки индуктивности: Z _ab = Z _bc = Z _ca = Z_Ф =+ jx_L = x_Le^+jπ/2. Поскольку система фазных напряжений на зажимах приемника всегда симметрична, так как она является симметричной системой линейных напряжений генератора, то векторная диаграмма фазных напряжений на рисунке 19 представляет собой симметричную звезду.

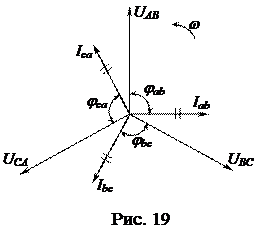Очевидно токи в фазах приемника будут одинаковы по величине 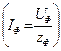и отставать от «своих» фазных напряжений на угол , как это показано на рисунке 19. Нетрудно убедиться, что система векторов фазных токов также симметрична.

Для установления количественных связей между фазными и линейными токами на рисунке 20 показано построение векторов линейных токов с использованием симметричной звезды векторов фазных токов без ее увязки с векторами напряжений.

Рис. 20

Сплошными линиями показаны векторы линейных токов , построенных по правилу сложения векторов методом многоугольника (треугольника) в соответствии с записью по первому закону Кирхгофа в виде:

.

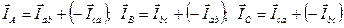Полученная симметричная звезда векторов линейных токов отстает от звезды векторов фазных токов на угол 30°.

Векторная диаграмма линейных токов может быть представлена более компактно в виде сторон правильного (равностороннего) треугольника (рис. 20), вершинами которого являются концы векторов фазных токов (эти векторы показаны пунктирными линиями).

При рассмотрении этого треугольника, сторонами которого являются векторы линейных токов, можно убедиться, что векторная сумма этих токов действительно равна нулю в соответствии с равенством (25).

Очевидно и при несимметричной нагрузке можно также показывать векторы линейных токов в виде векторного треугольника, вершинами которого будут концы векторов фазных токов, представленных в виде несимметричной звезды векторов.

Для определения соотношения линейных и фазных токов при симметричной нагрузке рассмотрим прямоугольный треугольник D mq 0 на рисунке 20. Он получается, если из вершины тупого угла равнобедренного треугольника опустить высоту, которая является и медианой, то есть отрезок (это катет, прилежащий к углу 30°). Гипотенуза рассматриваемого треугольника – отрезок . Можно представить отрезок как линию косинуса, то есть . Поскольку , то приравняв правые части последних равенств и сократив на 1/2, получим

(26)

.

Таким образом при симметричной нагрузке (и только при симметричной нагрузке) линейный ток в больше фазного тока ( = 1,73).

Рассмотрим частный случай несимметричной нагрузки – равномерную нагрузку. На рисунке 21 показана схема приемника, соединенного треугольником, у которого сопротивления фаз, а следовательно, и фазные токи равны друг другу (I_ab = I_bc = I_ba = I_Ф), а углы сдвига φ различны: φ_ab = 0, φ_bc = 0, φ_ca = – π/2.

На рисунке 22 показана векторная диаграмма рассматриваемой цепи. Система фазных напряжений представлена симметричной звездой векторов 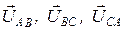. Токи в фазах и совпадают по фазе со «своими» напряжениями и сонаправлены с их векторами (φ_ab = 0, φ_bc = 0). Ве

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: