 |
Уравнения пограничного слоя Л. Прандтля
|
|
|
|
На тот факт, что влияние вязкости должно сказываться лишь вблизи обтекаемой стенки, было указано еще Д. М. Менделеевым (1880 г.) в его исследованиях по сопротивлению жидкостей движущимся телам. Математическая теория пограничного слоя была дана Л. Прандтлем.
При выводе уравнений пограничного слоя продольную (вообще говоря, криволинейную) координату х выбирают вдоль обтекаемой поверхности, а ось у - перпендикулярно к ней. Начало координат обычно удобно выбрать в передней критической точке, где набегающий поток раздваивается. Из - за малой толщины d пограничного слоя по сравнению с размерами обтекаемого тела можно пренебречь кривизной поверхности и рассмотреть выбранную систему координат как декартовую [x; y], рисунок 2.2.

Рисунок 2.2 - Ортогональная сетка координат [x, y]
Для установившегося движения вязкой жидкости уравнения Навье - Стокса (1.2) и уравнение непрерывности в случае плоского (двухмерного) потока принимают вид:
wx 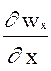 + wy
+ wy  = -
= - 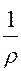
 + n(
+ n( +
+ 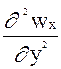 ),
),
wx  + wy
+ wy  = -
= - 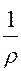
 + n(
+ n(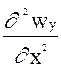 +
+ 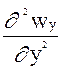 ),
),
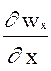 +
+  = 0.
= 0.
Учитывая, что внутри пограничного слоя значительные градиенты только продольной составляющей скорости wx, второе из написанных уравнений упрощается:
 =0.
=0.
Из этого следует важная особенность пограничного слоя: давление внешнего потока передается через пограничный слой без изменений. Можно показать также, что в первом уравнении член  весьма мал по сравнению
весьма мал по сравнению 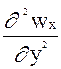 . В итоге получим систему уравнений для пограничного слоя Л. Прандтля:
. В итоге получим систему уравнений для пограничного слоя Л. Прандтля:
wx 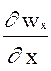 + wy + wy  = - = - 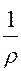 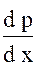 + n + n 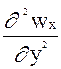 , ,
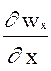 + +  = 0. = 0.
| } | (2.1) |
Результаты интегрирования этих гораздо более простых уравнений хорошо совпадают с экспериментальными данными.
Кроме того, следуя идее Л. Прандтля, продольное изменение давления (член - 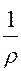
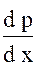 ) можно найти, рассматривая потенциальное течение в области 111 (рисунок 2.1), где справедливо уравнение Бернулли для идеальной жидкости
) можно найти, рассматривая потенциальное течение в области 111 (рисунок 2.1), где справедливо уравнение Бернулли для идеальной жидкости
|
|
|
U2 / 2 + p/r = const. (2.2)
Здесь U - скорость вне пограничного слоя в области 111 у данной точки обтекаемого тела. Дифференцируя последнее равенство по х, получим
U  +
+ 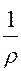
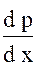 = 0,
= 0,
или
- 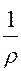
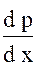 = U
= U  .
.
Учитывая это, перепишем систему уравнений Прандтля (2.1) в виде:
wx 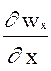 + wy + wy  = U = U  + n + n 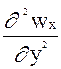 , ,
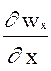 + +  = 0. = 0.
| } | (2.3) |
В этих уравнениях распределение скоростей U(x) во внешнем потенциальном потоке на границе пограничного слоя можно получить. решая задачу обтекания тела потоком идеальной жидкости. а затем осуществить "стыковку" этого решения с течением вязкой жидкости в пограничном слое.
Граничные условия для системы уравнений пограничного слоя предполагают, во - первых, равенство нулю вектора скорости на поверхности обтекаемого тела, т. е.
wxôy=0 = wyôy = 0 (2.4)
из условий непроницаемости стенки и "прилипания" к ней вязкой жидкости.
Во - вторых, "стыковка" на внешней границе пограничного слоя предполагает равенство скорости частиц вязкой жидкости и скорости U(x) внешнего (потенциального) потока идеальной жидкости. Хотя, формально влияние пристеночного торможения жидкости сказывается на любом расстоянии от стенки, так что, строго говоря, это условие записывается в виде
wxôy® ¥ = U(x) (2.5)
и предполагает асимптотический переход к скорости внешнего потока. Однако, с целью упрощения, более часто второе граничное условие задается для пограничного слоя "конечной толщины d", под которым подразумевают слой жидкости, в котором на расстоянии d от стенки происходит изменение скорости от нуля (на стенке) до wx = U(x) (на расстоянии d от стенки), при условии плавности такого перехода
wxôy = d = U(x),  ôy = d = 0. (2.51)
ôy = d = 0. (2.51)
В качестве d можно, например, принять расстояние от стенки, на котором скорость отличается от скорости внешнего потока на 1%, когда wx(x) ïy=d= 0,99U(x).
|
|
|
Расплывчатость такой оценки очевидна. Поэтому используются интегральные, менее наглядные, но более строгие оценки.
Толщина вытеснения (рисунок 2.3)
d * = [ò(U - wx)dy]/U = ò [1 - wx(y)/U]dy.

Рисунок 2.3 - Поле скоростей в пограничном слое:
d - толщина пограничного слоя; d* - толщина вытеснения
Интеграл ò(U - wx)dy представляет собой разность между расходами жидкости в пограничном слое d, если бы скорость по всему его течению не уменьшалась из - за вязкости, а оставалась бы равной U, и действительным расходом (заштрихованная часть эпюры скоростей справа), т. е. представляет собой уменьшение расхода жидкости в пограничном слое из - за вязкости. Разделив этот интеграл на величину U, получим некоторую величину d*, через которую и протекал бы недостающий расход (перекрестная штриховка). На d* оттесняются от поверхности тела линии тока невозмущенного течения из - за вязкого торможения.
Аналогичные характеристики можно ввести для импульса и энергии потока:
d
d** = ò [(wx(y)/U)(1-wx(y)/U)]dy- толщина потери импульса;
0
d
d***= ò[(wx(y)/U)(1-w2x(y)/U2)]dy- толщина потери энергии.
|
|
|


