 |
В) Тригонометрические функции
|
|
|
|
Исторические сведения
Большинство математических понятий прошли долгий путь развития. Сложный путь прошло понятие функции. Оно уходит корнями в ту далекую эпоху, когда люди впервые поняли, что окружающие их явления взаимосвязаны. Они еще не умели считать, но уже знали, что чем больше оленей удастся убить на охоте, тем дольше племя будет избавлено от голода; чем сильнее натянута тетива лука, тем дальше полетит стрела; чем дольше горит костер, тем теплее будет в пещере. С развитием скотоводства, земледелия, ремесел и обмена увеличивалось количество известных людям зависимостей между величинами.
Идея зависимости некоторых величин восходит к древнегреческой науке. Но греки рассматривали лишь вопросы, имеющие “геометрическую” природу, и не ставили вопроса об общем изучении различных зависимостей. Графическое изображение зависимостей широко использовали Г.Галилей (1564–1642), П.Ферма (1601–1665) и Р.Декарт (1569–1650), который ввел понятие «переменной величины». По определению Декарта: «Функцией переменной величины называется количество, образованное каким угодно способом из этой переменной величины и постоянных».
Развитие механики и техники потребовало введения общего понятия функции, что было сделано немецким философом и математиком Г.Лейбницем. Следующий шаг в развитии понятия функции сделал ученик Бернулли, член Петербургской Академии наук Леонард Эйлер (1707 – 1783). Он писал: “Величины, зависящие от других так, что с изменениями вторых изменяются и первые, принято называть их функциями”.В общем виде понятие обобщенной функции было введено французом Лораном Шварцем. В 1936 году, 28-летний советский математик и механик С. Л. Соболев первым рассмотрел частный случай обобщенной функции. Итак, знание законов природы дало человеку возможность объяснять и предсказывать ее разнообразнейшие явления.
|
|
|
Определение функции
Функция - одно из основных математических и общенаучных понятий,выражающее зависимость одних переменных величин от других. Оно сыграло и поныне играет большую роль в познании реального мира.
Определение. Числовой функцией с областью определения D называется соответствие, при котором каждому числу x из множества D сопоставляется по некоторому правилу единственное число y, зависящее от x. Принято называть x независимой переменной или аргументом, а у — зависимой переменной или значением функции.
Записывают указанное соотношение между x и у в общем виде так: у = f (x) или у = F (x) и т. п.
График функции y = f (х) - это множество всех точек плоскости, координаты (х, у) которых удовлетворяют соотношению y = f(x).
Способы задания функции:
1) аналитический (с помощью формулы);
2) графический;
3) табличный;
4) словесный.
Функции, изучаемые в школе:
1) линейная y = ax + b;
2) квадратичная y = ax2 + bx + c;
3) обратная пропорциональность 
;
4) корень n - степени 
;
5) модуль y = | x |;
6) тригонометрические y = sinx, y = cosx, y = tgx, y = ctgx;
7) показательная 
;
8) логарифмическая 
.
Примеры применения различных функций
В жизни, технике, природе
В наши дни без функций невозможно не только рассчитать космические траектории, работу ядерных реакторов, и бег океанской волны и закономерности развития циклона, но и экономично управлять производством, распределением ресурсов, организацией технологичных процессов, прогнозировать течение химических реакций или изменение численности различных взаимосвязанных в природе видов животных и растений, потому что все это – динамические процессы, которые описывает функция.
А) Линейная функция
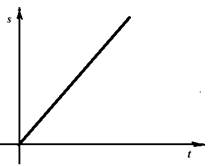Функция y = a x + b называется линейной потому, что ее график есть прямая линия. Характеристическим свойством линейной функции является изменение функции пропорционально изменению аргумента. Поэтому с помощью линейной функции описываются пропорциональные зависимости. Например, при равномерном движении с постоянной скоростью v пройденный путь s пропорционален времени t и выражается формулой s = v t, т.е. s – линейная функция t.
|
|
|
Пример линейной функции дает зависимость между различными шкалами температур. Абсолютная температура Т (по Кельвину) связана с температурой tͦC на шкале Цельсия формулой t = T + 273 ͦ. Другой пример – напряжение в электрической цепи прямо пропорционально силе тока U = IR. Можно много приводить примеров линейных зависимостей в физике, химии. Рассмотрим задачу на линейное расширение тел.
Задача. При температуре 0оС рельс имеет длину l 0 = 12,5 м. при возрастании температуры происходит тепловое расширение рельса и его длина, выраженная в метрах, меняется по закону l (t о) = l 0(1 +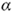 
t о),где 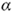= 1,2 ˖ 10–5 – коэффициент теплового расширения в градусах Цельсия в минус первой степени, t о – температура (в градусах Цельсия). При какой температуре рельс удлинится на 6 мм. Ответ выразить в градусах Цельсия.
Решение. Выразим из заданной формулы t: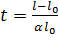 
.
Заметим,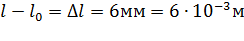 
,
тогда 
Ответ: 40.
Б) Квадратичная функция
Графиком квадратичной функции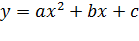 
является парабола.
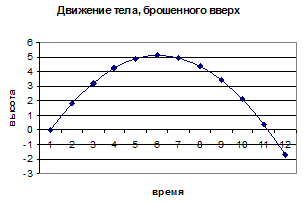Хорошо известно, что траектория камня, брошенного под углом к горизонту, летящего футбольного мяча или артиллерийского снаряда будет параболой (при отсутствии сопротивления воздуха). Однако мало кто знает, что зона достижимости для пущенных нами камней вновь будет параболой. В данном случае мы говорим об огибающей кривой траекторией камней, выпущенных из данной точки под разными углами, но с одной и той же начальной скоростью. Если рассматривать такую огибающую в пространстве, то возникнет поверхность, образованная вращением этой параболы вокруг ее оси. Такая поверхность носит название параболоида вращения.
Парабола обладает оптическим свойством: все лучи, исходящие из источника света, находящегося в фокусе параболы, после отражения оказываются направленными параллельно ее оси. Это свойство параболы используется при изготовлении прожекторов, автомобильных фар, карманных фонариков, зеркала которых имеют вид параболоидов вращения.
|
|
|
Очевидно, что пучок параллельных лучей, двигающийся вдоль оси параболы, отражаясь, собирается в ее фокусе. На этом основана идея телескопов – рефлекторов, зеркала которых выполнены в виде параболоидов вращения. Любопытно, что параболоид вращения образует поверхность жидкости в цилиндрическом сосуде, если его вращать относительно своей оси.
в) Тригонометрические функции
Различные колебания окружают нас на каждом шагу. Механические колебания применяются для просеивания материалов на виброситах, безболезненного высверливания отверстий в зубах. Акустические колебания нужны для приема и воспроизведения звука, а электромагнитные – для радио, телевидения, связи с космическими ракетами. С помощью электромагнитных колебаний учеными были получены снимки обратной стороны Луны и вечно закрытой облаками Венеры. Колебания сопровождают и биологические процессы, например, слух, зрение, работу сердца и мозга.
Но колебания не всегда полезны. Вибрация станка может привести к браку; вибрация самолетных крыльев при неблагоприятных условиях может привести к катастрофе. Если колебания под контролем человека полезны, то, вырвавшись из-под этого контроля, они превращаются в опасного врага. Надо уметь изучать колебания, знать их свойства.
Самый удобный математический метод для описания колебаний в применении тригонометрических функций. График функции y = sinx называется синусоида.
Г) Показательная функция
Показательная функция очень часто реализуется в физических, биологических и иных законах. В жизни нередко приходится встречаться с такими фактами, когда скорость изменения какой-либо величины пропорциональна самой величине. В этом случае рассматриваемая величина будет изменяться по закону, имеющему вид показательной функции у=у0аx.
Эти процессы называются процессами органического роста или органического затухания.
Например, рост бактерий в идеальных условиях соответствует процессу органического роста; радиоактивный распад вещества – процессу органического затухания. Законам органического роста подчиняется рост вклада в банке, восстановление гемоглобина в крови донора или раненого. Закон органического роста выражается формулой: N = N0ekt.
|
|
|
Описание радиоактивного распада так же связано с показательной функцией. Количество распадающегося за единицу времени вещества всегда пропорционально имевшемуся количеству вещества. Радий распадается в зависимости от времени по закону М = М0е-kt, где: Мо – начальное количество радия, k – некоторый коэффициент.
|
|
|
