 |
Функциональные зависимости в повседневной жизни
|
|
|
|
В повседневной жизни мы постоянно сталкиваемся с функциональными зависимостями. Мы нашли множество примеров функций, которые изобразили с помощью графиков.
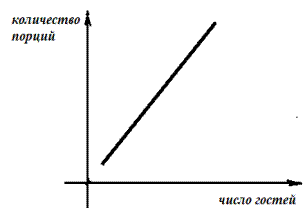
Пример 1. Рассмотрим деление праздничного торта между гостями. Отчего зависит количество порций?– от числа гостей. А от чего зависит вес порции? – тоже от числа гостей.
− В первом случае, чем больше гостей, тем на большее количество порций мы должны разделить торт (рис. 1).
 Здесь наглядно можно представить прямую пропорциональную зависимость.
Здесь наглядно можно представить прямую пропорциональную зависимость.
|
|
Во втором случае, чем больше гостей, тем меньше вес порции.Здесь мы видим
|
 Пример 2. Мы живём в век информационных технологий. Ежедневно мы получаем массу информации из различных источников: телевидения, радио, газет, журналов, и, конечно, из Интернета. Известно, что объём информации каждые пять лет увеличивается в два раза.
Пример 2. Мы живём в век информационных технологий. Ежедневно мы получаем массу информации из различных источников: телевидения, радио, газет, журналов, и, конечно, из Интернета. Известно, что объём информации каждые пять лет увеличивается в два раза.
|
|
|
|
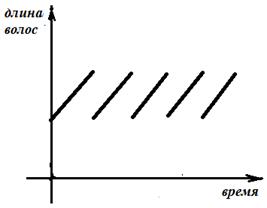 Пример 3. На голове человека растут волосы, которые регулярно стригут.
Пример 3. На голове человека растут волосы, которые регулярно стригут.
График полученной зависимости (при условии, что стрижку делают регулярно) похож на функцию дробной части числа, смещённую на a единиц вверх: 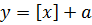 (рис. 4).
(рис. 4).
|
 Пример 4. За время обучения в школе каждый год переходим в следующий класс.
Пример 4. За время обучения в школе каждый год переходим в следующий класс.
Такая зависимость сходна с функцией целой части числа 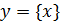 на ограниченном промежутке (рис. 5).
на ограниченном промежутке (рис. 5).
|
Пример 5. Изменение температурного режима в нашей климатической зоне подчиняется законам тригонометрических функций (рис. 6)
|
|
|

|
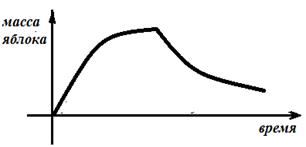 Пример 6. Садово-огородные процессы тоже можно представить в виде функции и построить график. К примеру, яблоко росло, зрело, потом его высушили (рис. 7). Получили некоторую кусочную функцию.
Пример 6. Садово-огородные процессы тоже можно представить в виде функции и построить график. К примеру, яблоко росло, зрело, потом его высушили (рис. 7). Получили некоторую кусочную функцию.
|
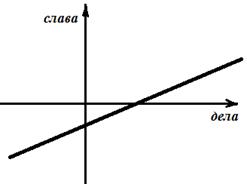 Пример 7. Графиком можно проиллюстрировать смысл любой пословицы.
Пример 7. Графиком можно проиллюстрировать смысл любой пословицы.
Вот, например, пословица – «Каково жизнь проживешь, такую славу наживешь» на графике будет выглядеть следующим образом (рис.8):
|
 Или такая пословица – «Пересев хуже недосева» на графике будет выглядеть так (рис. 9):
Или такая пословица – «Пересев хуже недосева» на графике будет выглядеть так (рис. 9):
|
Любой чертеж графика функции начинается с координатных осей.
Кстати: Чертежи бывают двухмерными и трехмерными.
Сначала рассмотрим двухмерный случай декартовой прямоугольной системы координат:
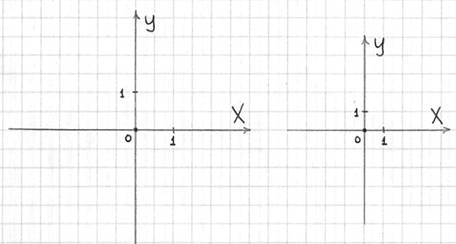
1) Чертим координатные оси. Ось  называется осью абсцисс, а ось
называется осью абсцисс, а ось 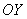 – осью ординат. Чертить их всегда стараемся аккуратно и не криво. Стрелочки тоже не должны напоминать бороду Папы Карло.
– осью ординат. Чертить их всегда стараемся аккуратно и не криво. Стрелочки тоже не должны напоминать бороду Папы Карло.
2) Подписываем оси буквами «икс» и «игрек». Не забываем подписывать оси.
3) Задаем масштаб по осям: рисуем ноль и две единички. При выполнении чертежа самый удобный и часто встречающийся масштаб: 1 единица = 1 клеточка. Однако время от времени случается так, что в чертеже необходимо отмечать дробные величины, тогда допускается масштаб: 1 единица = 2 клеточка. Редко, но бывает, что масштаб чертежа приходится уменьшать (или увеличивать) еще больше
|
|
|
НЕ НУЖНО «строчить из пулемёта» …-5, -4, -3, -1, 0, 1, 2, 3, 4, 5, …. Ибо координатная плоскость – не памятник Декарту, а студент – не голубь. Ставим ноль и две единицы по осям.
Предполагаемые размеры чертежа лучше оценить еще ДО построения чертежа. Кстати, о сантиметрах и тетрадных клетках. Правда ли, что в 30 тетрадных клетках содержится 15 сантиметров? Отмерьте в тетради для интереса 15 сантиметров линейкой. В СССР, возможно, это было правдой… Интересно отметить, что если отмерить эти самые сантиметры по горизонтали и вертикали, то результаты (в клетках) будут разными! Строго говоря, современные тетради не клетчатые, а прямоугольные. Возможно, это покажется ерундой, но, чертить, например, окружность циркулем при таких раскладах очень неудобно. Это печалька нашего времени!!
Линейная функция задается уравнением 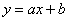 . График линейной функций представляет собой прямую. Для того, чтобы построить прямую достаточно знать две точки.
. График линейной функций представляет собой прямую. Для того, чтобы построить прямую достаточно знать две точки.
Пример 1 Построить график функции 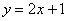 . Найдем две точки. В качестве одной из точек выгодно выбрать ноль.
. Найдем две точки. В качестве одной из точек выгодно выбрать ноль.
Если 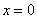 , то
, то 
Берем еще какую-нибудь точку, например, 1.
Если 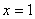 , то
, то 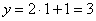
При оформлении заданий координаты точек обычно сводятся в таблицу:
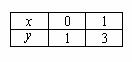 А сами значения рассчитываются устно или на черновике.
А сами значения рассчитываются устно или на черновике.

1) Линейная функция вида 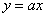 (
( ) называется прямой пропорциональностью. Например,
) называется прямой пропорциональностью. Например, 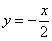 . График прямой пропорциональности всегда проходит через начало координат. Таким образом, построение прямой упрощается – достаточно найти всего одну точку.
. График прямой пропорциональности всегда проходит через начало координат. Таким образом, построение прямой упрощается – достаточно найти всего одну точку.
2) Уравнение вида 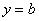 задает прямую, параллельную оси
задает прямую, параллельную оси  , в частности, сама ось
, в частности, сама ось  задается уравнением
задается уравнением  . График функции строится сразу, без нахождения всяких точек. То есть, запись
. График функции строится сразу, без нахождения всяких точек. То есть, запись 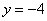 следует понимать так: «игрек всегда равен –4, при любом значении икс».
следует понимать так: «игрек всегда равен –4, при любом значении икс».
3) Уравнение вида  задает прямую, параллельную оси
задает прямую, параллельную оси 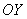 , в частности, сама ось
, в частности, сама ось 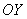 задается уравнением
задается уравнением 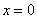 . График функции также строится сразу. Запись
. График функции также строится сразу. Запись 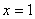 следует понимать так: «икс всегда, при любом значении игрек, равен 1».
следует понимать так: «икс всегда, при любом значении игрек, равен 1».
Некоторые спросят, ну зачем вспоминать 6 класс?! Так-то оно, может и так, только за годы практики я встретила добрый десяток студентов, которых ставила в тупик задача построения графика вроде 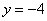 или
или 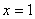 .
.
Построение прямой – самое распространенное действие при выполнении чертежей.
|
|
|
Рассмотрим знаменитый случай: 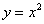
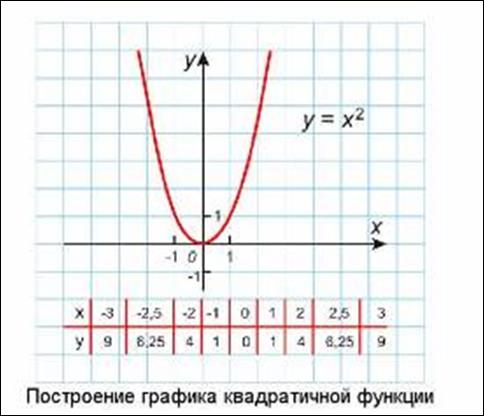
Вспоминаем некоторые свойства функции 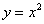 .
.
Область определения – любое действительное число (любое значение «икс»). Что это значит? Какую бы точку на оси  мы не выбрали – для каждого «икс» существует точка параболы. Математически это записывается так:
мы не выбрали – для каждого «икс» существует точка параболы. Математически это записывается так: 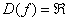 . Область определения любой функции стандартно обозначается через
. Область определения любой функции стандартно обозначается через  или
или 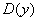 . Буква
. Буква 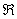 обозначает множество действительных чисел или, проще говоря, «любое икс» (когда работа оформляется в тетради, пишут не фигурную букву
обозначает множество действительных чисел или, проще говоря, «любое икс» (когда работа оформляется в тетради, пишут не фигурную букву 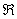 , а жирную букву R).
, а жирную букву R).
Область значений – это множество всех значений, которые может принимать переменная «игрек». В данном случае:  – множество всех положительных значений, включая ноль. Область значений стандартно обозначается через
– множество всех положительных значений, включая ноль. Область значений стандартно обозначается через  или
или 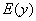 .
.
Функция 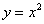 является чётной. Если функция является чётной, то ее график симметричен относительно оси
является чётной. Если функция является чётной, то ее график симметричен относительно оси 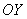 . Это очень полезное свойство, которое заметно упрощает построение графика
. Это очень полезное свойство, которое заметно упрощает построение графика
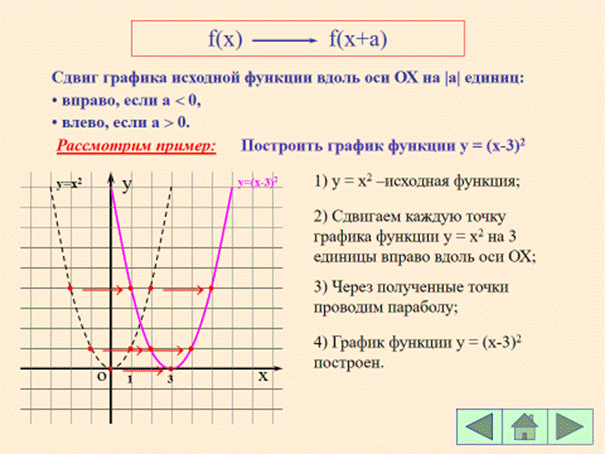
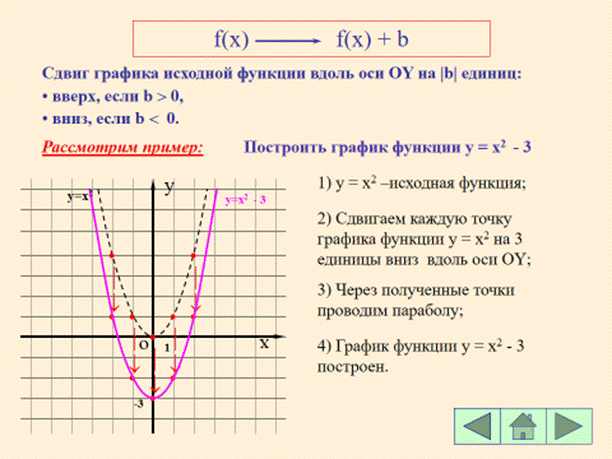
Постройте график функции с использованием движения графиков:
1. y =(x+2)2 (f(x) ® f(x+a))
2. y = x2+1 (f(x) ® f(x) + b)
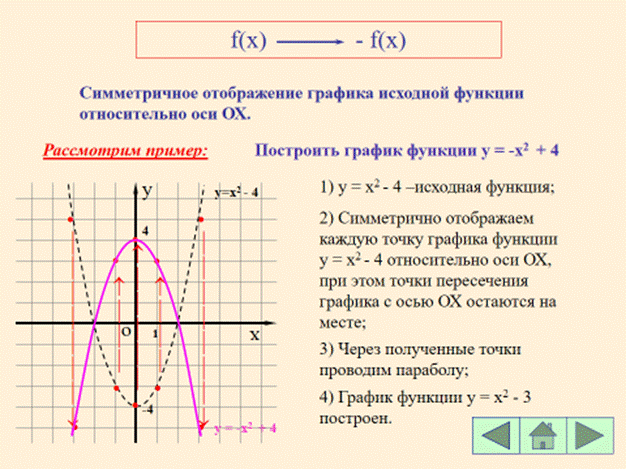
3. y = -x2 (f(x) ® - f(x))
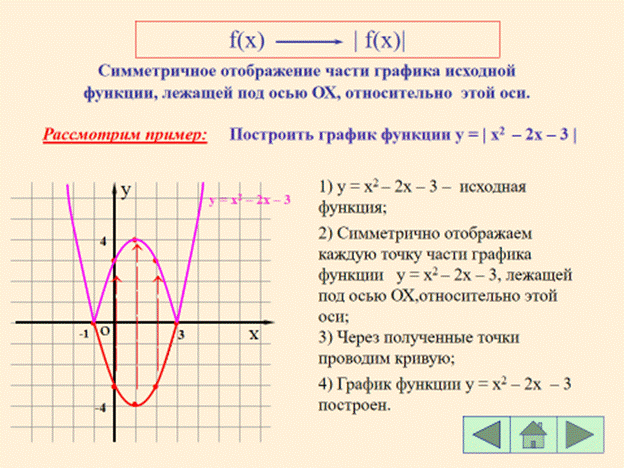
4. y =|x2 - 4| (f(x) ® f(x) + b, f(x) ® |f(x)|)
Постройте график функции с использованием движения графиков:
1. y = - (x - 1)2 (f(x) ® f(x+a), f(x) ® - f(x))
2. y = |x2 - 3| - 1 (f(x) ® f(x) + b, f(x) ® - f(x), f(x) ® f(x) + b)
3. y = x2 – 4х + 5
Постройте график функции
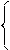 х2-1, если х
х2-1, если х  0
0
f(x)= (x-1)2,если х>0
При каких значениях х выполняется неравенство у 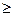 0
0
Первым графиком является парабола. Построим её часть (х  0) путем сдвига вниз на 1 графика
0) путем сдвига вниз на 1 графика
у= х2.
| х | -1 | -2 | -3 | -4 | |
| у | -1 |
Вторым графиком является тоже парабола. Построим её часть (х>0)путем сдвига вдоль оси ох вправо на 1 графика у= х2.
| х | |||||
| у |
Ответ: при у>0, x<-1,0<x<1 и x>1 
|
|
|


