 |
Описание лабораторной установки.
|
|
|
|
Описание лабораторной установки.
Общий вид автомата для загрузки деталей пневмоманипулятором представлен на рисунке 4. 9.
 |

Рисунок 4. 9 – Общий вид установки для автоматической загрузки деталей
Установка состоит из манипулятора 1, командоаппарата 2, блока управления 3, блока питания 4, пневмораспределителей 5.
Порядок выполнения работы
1. Привести манипулятор в исходное состояние:
– поднять схват вверх;
– перевести руку манипулятора влево до упора.
2. Включить установку в сеть 220 В. Переключатель «Автомат – Полуавтомат» перевести в положение «Полуавтомат».
3. Включить секундомер и одновременно нажать кнопку «Пуск» на пульте управления. Определить цену деления лимба командоаппарата.
4. Включить компрессор пневмосети и нажать кнопку «Пуск» на блоке управления. Определить последовательность работы узлов автомата.
5. Переключатель «Автомат – Полуавтомат» перевести в положение «Автомат».
6. При помощи секундомера определить время начала и конца действия каждого узла автомата в процессе загрузки деталей за один цикл.
7. Пункт 6 повторить 3 раза и определить среднее время работы отдельных узлов.
8. По полученным данным построить циклограмму работы автомата.
Содержание отчета
1. Схема манипулятора.
2. Циклограмма работы автомата.
Контрольные вопросы к лабораторной работе
1. Каковы достоинства и недостатки кулачковых систем управления?
2. В чем состоят основные преимущества систем с командоаппаратом по сравнению с кулачковыми?
3. Чем отличаются копировальные системы прямого действия от систем непрямого действия?
|
|
|
4. Что такое циклограммы и для чего они предназначены?
5. Какие системы управления называются циклическими и какие ациклическими?
6. Какая система управления ипользуется в лабораторном макете?
Литература
Автоматическая загрузка технологических машин. Справочник / И. С. Бляхаров, А. А. Иванов и др. – М.: Машиностроение, 1990 – 400 с.
Лабораторная работа № 5
СИНТЕЗ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ (САУ) НА ЛОГИЧЕСКИХ ЭЛЕМЕНТАХ
Цель работы: изучить конструкцию пневмореле РУП-1 и способы реализации логических функций; изучить принципы построения схем САУ на логических элементах; осуществить синтез однотактной САУ с помощью пневмоэлементов.
Оборудование и принадлежности к работе
1. Лабораторный стенд №1 – 1 шт.;
2. Лабораторный стенд №2 – 1 шт.;
3. Компрессор – 1 шт.;
4. Соединительные трубки
Основные положения
При автоматическом управлении различными технологическими процессами, рабочими машинами и механизмами широко применяются логические элементы (ЛЭ). Логические элементы вырабатывают сигнал на выходе в зависимости от определенных сочетаний сигналов на входе и реализуют логические функции, которые, как и их аргументы, имеют значения 0 или 1. Символами «0» обозначают минимальный уровень (сигнала нет), а «1» – максимальный уровень сигнала (сигнал есть).
Логической системой управления называют систему, построенную из логических элементов с целью реализации заданной функции. Процесс синтеза СУ можно выполнять различными методами, и в общем случае его подразделяют на следующие этапы: составление формализованного описания работы системы по известной циклограмме или словесному описанию; составление логических уравнений; упрощение логических уравнений; построение принципиальной схемы.
|
|
|
В зависимости от условий работы различают однотактные (комбинационные) и многотактные (последовательные) СУ.
Однотактными называются такие системы, у которых комбинация выходных сигналов в любой промежуток времени (в любом такте) однозначно определяется комбинацией сигналов, поступающих на вход в течение этого же промежутка времени (такта) и не зависит от комбинации сигналов, поступивших на вход в предыдущие промежутки времени.
Выходные сигналы однотактных систем полностью определяются состояниями входов, существующими в данный момент времени, поэтому подобные системы называются иногда автоматами без памяти.
Многотактными (последовательностными) называются такие системы, у которых комбинация сигналов определяется не только состоянием входов в данный момент времени, но и зависит также от значений выходных сигналов в предыдущих тактах. Любая последовательностная схема автомата может быть реализована с помощью набора логических операций и элементов памяти. В структурном отношении последовательностная схема состоит из двух составляющих: комбинационной логической схемы и памяти, через которую реализуется обратная связь (рис. 5. 1).
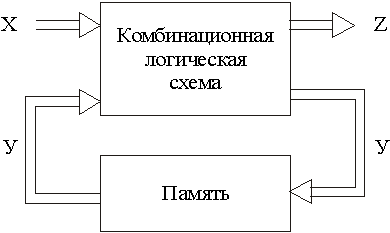
Рисунок 5. 1 – Последовательностная схема
На входы комбинационной схемы подаются внешние сигналы Х и внутренние вторичные сигналы Y, которые снимаются с выходов памяти. В результате этого возникают выходные сигналы Z и внутренние сигналы Y, подаваемые на вход запоминающего устройства. Запоминающее устройство может задерживать сигнал Y на величину автоматного времени или запоминать и хранить его до тех пор, пока не поступят новые сигналы. Для реализации запоминающих устройств широко используются триггерные схемы различного класса.
Оптимальные условия (или близкие к ним) систем управления можно построить, используя методы математической логики. Математическим аппаратом анализа и синтеза СУ является двузначная алгебра логики.
Основные логические функции их преобразование и реализация.
Логические функции (ЛФ) представляют собой зависимость выходных переменных от входных, простейшими логическими функциями являются ЛФ одной и двух переменных. На их основании можно определить ЛФ различной сложности от любого числа переменных. Реализацию ЛФ осуществляют контактными или бесконтактными логическими элементами. Основные логические функции приведены в таблице 5. 1.
|
|
|
Для преобразования логических функций используют основные законы алгебры логики:
переместительный: X1·X2 = X2·X1
сочетательный: (Х1·Х2) ·Х3 = Х1· (Х2·Х3);
(Х1 V Х2 ) V Х3 = Х1 V (Х2 V Х3 )
распределительный: Х1· (Х2 V X3) = X1·Х2 V Х1·Х3
повторения: Х·Х∙ Х... ·Х = Х; Х V Х V X…V X = X
инверсии 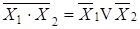 ;
; 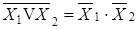
поглощения Х1 V Х1·Х2 = Х1; X1·(X1 V X2) = X1
склеивания 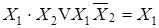 ;
; 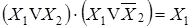
Таблица 5. 1 – Реализация и обозначение основных логических операций
| Операция | Обозначение при реализации | |
| На контактах реле | На бесконтактных элементах | |
| Повторение «ДА» f = x | 
| 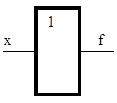
|
Инверсия «НЕ»
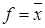
| 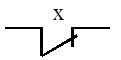
| 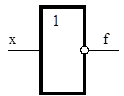
|
| Конъюнкция «И» f = x1·x2 | 
| 
|
| Дизъюнкция «ИЛИ» f = x1Vx2 | 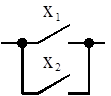
| 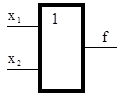
|
Штрих Шеффера
«И-НЕ»
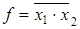 ; ;

| 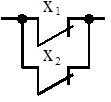
| 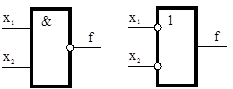
|
Стрелка Пирса
«ИЛИ-НЕ»
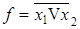 ; ;

| 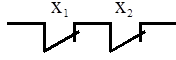
| 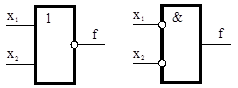
|
Импликация
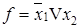
| 
| 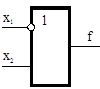
|
Запрет
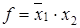
| 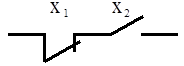
| 
|
Эквивалентность

| 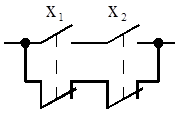
| 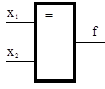
|
Неэквивалентность
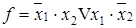
| 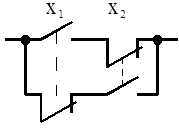
| 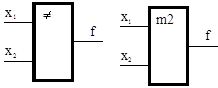
|
Логические операции умножения, сложения, инверсии и другие являются взаимно зависимыми и выражаются друг через друга.
Системы логических операций, с помощью которых можно выразить все другие операции, называют функционально полными. Так простейшими функционально полными будут системы: конъюнкции и инверсии; дизъюнкции и инверсии, операции стрелка Пирса («ИЛИ-НЕ») и др.
Наибольшее распространение получили три логических функции («И», «ИЛИ», «НЕ»). Любая логическая функция (функция любой сложности и любого количества переменных) может иметь множество равносильных формул, отличающихся используемым видом элементарных функций. Все это множество при помощи формул алгебры логики может быть приведено к форме, представляющей собой дизъюнкцию элементарных конъюнкций и называемой дизъюнктивной нормальной формой (ДНФ) или конъюнкцию элементарных дизъюнкций – конъюнктивно нормальную форму (КНФ).
|
|
|
Кроме описанного метода задания логических функций алгебраическим способом они могут задаваться и другими способами. Они могут быть изображены с помощью таблиц истинности.
Таблицы истинности состоят из n+1 столбцов, где n столбцов отводятся для значений переменных изображаемой функции, а последний столбец – для значений самой функции.
Число строк таблицы 2n. В каждую строку записывают одну из возможных комбинаций значений переменных и соответствующее ей значение функций (табл. 5. 2).
Методика перехода от табличного изображения к алгебраическому в форме ДНФ, следующая: выделить строки с единичными значениями логической функции, выписать для каждой отмеченной строки элементарные конъюнкции переменных, соединить их знаком дизъюнкции. Алгебраическое изображение логической функции, представленной в таблице в форме дизъюнкции элементарных конъюнкций имеет вид:
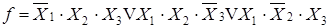
| (5. 1) |
Такая запись называется канонической, так как каждый член выражения включает все три переменных (Х1, Х2, Х3).
Для записи в форме КНФ необходимо выделить строки с нулевым значением булевой функции, выписать из каждой отмеченной строки элементарные дизъюнкции инверсий переменных и соединить их знаком конъюнкции. Из таблицы получим:
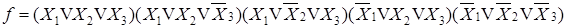
|
Если в таблице истинности число строк с единичным и нулевым значениями функции одинаково, то безразлично, по какой форме записывать. Однако, если в столбце, соответствующем значениям функции, преобладают единицы, то проще получать функцию по строкам, соответствующим нулевым значениям функции.
Синтез однотактных САУ
Задачу синтеза можно сформулировать следующим образом: при заданных входных переменных и известной выходной функции спроектировать устройство, которое реализует эту функцию.
Задачу анализа рассмотрим на примере схемы на контактных элементах, которая управляет включением лампочки y (рисунок 5. 2).
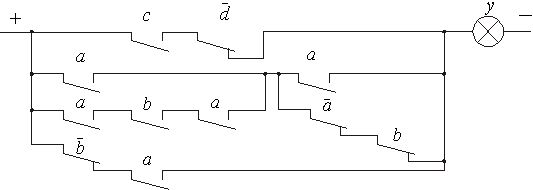
Рисунок 5. 2 – Контактная схема
Представим заданную схему в виде функции алгебры логики (ФАЛ):
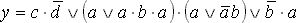
Применяя законы и правила алгебры логики произведем минимизацию функции:
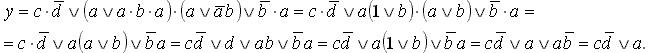
Построим минимизированную функцию на контактных и бесконтактных элементах (рисунок 5. 3)

Рисунок 5. 3 – Минимизированная схема управления
Рассмотрим метод синтеза однотактных систем управления (СУ) на примере построения СУ пневмоцилиндром, шток которого выдвигается при подаче двух из трех входных сигналов Х1, X2 и Х3 (рисунок 5. 4).
По условиям функционирования СУ три входных устройства не могут быть включены одновременно. Входными сигналами будут являться, например, сигналы от датчиков 1, 2, 3 положения детали на зажимном приспособлении станка. Если одна из возможных деталей 5 будет правильно установлена в приспособлении, т. е. будет подано 2 из 3 сигналов, то произойдет ее зажим при помощи пневмоцилиндра 4.
|
|
|
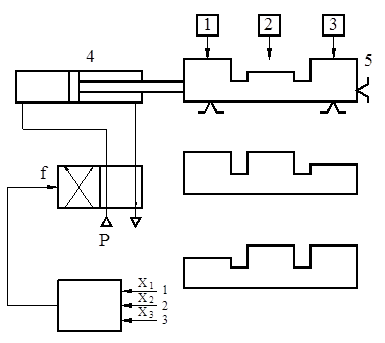
Рисунок 5. 4 – Схема работы САУ зажимным приспособлением
По заданным условиям работы составляется таблица состояний, т. е. таблица истинности. В таблицу состояний записываются все возможные комбинации входных переменных (Х1, X2 и Х3), причем для каждой комбинации поставляется соответствующее значение выходной функции f («0» или «1»). Условные состояния отмечаются в таблице, например, прочерками, с их помощью можно упростить структуру СУ путем задания значения выхода (0 или 1) на дальнейших этапах, исходя из получения более простого выражения для выходной функции (табл. 5. 2).
Таблица 5. 2
| X1 | X2 | X3 | f |
В соответствии с правилами перехода от таблицы истинности к алгебраической форме записи, для данного примера запишем:
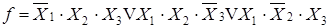
| (5. 2) |
Записанная по таблице состояний функция обычно содержит избыточность.
Построим структурную схему, реализующую данную функцию (рисунок 5. 5).

Рисунок 5. 5 – Структурная схема САУ зажимным приспособлением
Получается очень большой набор элементов, поэтому функцию необходимо упростить (минимизировать).
Под минимизацией понимают сведение к минимуму числа членов логической функции, числа переменных в каждом члене и числа логических знаков, т. е. в конечном итоге числа логических элементов, необходимых для построения заданной СУ. Синтез можно осуществлять несколькими способами.
1-ый способ – алгебраический. Из рассмотрения логического уравнения и условного состояния, которое по условиям функционирования СУ невозможно (X1 = 1, X2 = 1, Х3 = 1) можно сделать вывод, что если задать для него значение функции, равное 1, и ввести соответствующий член в логическую функцию, то он будет отличаться от каждого из имеющихся значением одной переменной. Это позволит, используя соотношения алгебры логики, упростить выражения.
Обозначим соответствующее состояние выходной функции 1* (табл. 5. 3, последняя строка) и соответствующим образом перепишем формулу (5. 2)
Таблица 5. 3
| X1 | X2 | X3 | f |
| 1* |
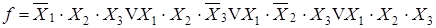
| (5. 3) |
Учитывая закон повторения, запишем
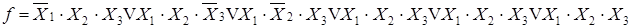
После преобразования с использованием закона склеивания или поглощения запишем в виде:
| f = X2 X3V X1 X3 V X1 X2 | (5. 4) |
2-ой способ. Рассмотрим синтез однотактных СУ с помощью матриц Карно. Матрицы Карно изображаются в виде прямоугольников, содержащих 2n, клеток, где n – число переменных. Число столбцов определяется как 2m, а число строк – как 2n-m, где 1 ≤ m ≤ n. Каждой клетке матрицы соответствует один член ДНФ (или каждое состояние в таблице истинности). Столбцы и строки в матрицах обозначают таким образом, чтобы соседние клетки представляли собой соседние состояния переменных, т. е. состояния, отличающиеся значением одной переменной. На рисунке 5. 6а, б показаны матрицы Карно для двух входных переменных, на рисунках 5. 6в, г – для трех (на рисунках а и в в клетки вписаны комбинации состояний входных переменных, на рисунках б и г – соответствующие им комбинации состояний входных сигналов).
Для рассматриваемого примера (5. 3), то есть с уже добавленным состоянием (X1 = 1, X2 = 1, Х3 = 1), матрица имеет следующий вид (рис. 5. 6д). Здесь в каждую клетку вписаны значения функции для соответствующих комбинаций состояний входных переменных).
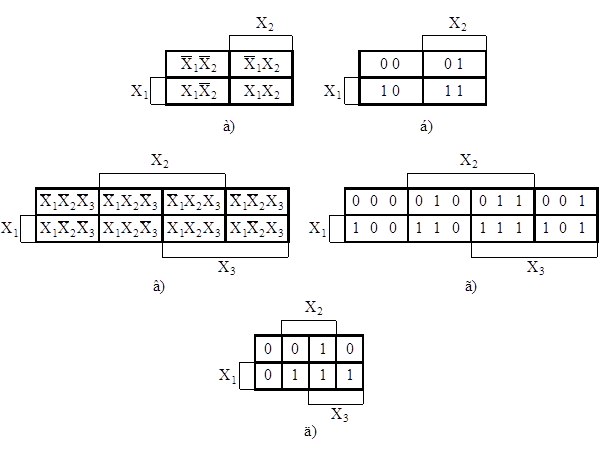
Рисунок 5. 6 – Матрицы Карно для двух переменных (а, б), для трех переменных (в, г)
и для рассматриваемого примера (д)
Учитывая, что расположенные рядом клетки отличаются одной переменной, на основе матрицы (карты) Карно можно записать упрощенное выражение выходной функции. Для этого соседние клетки объединяют в контур. В контур объединяют клетки, содержащие 1 или 0 (в зависимости от того, какую функцию минимизируем, ДНФ или КНФ). Площадь любого контура должна быть симметричной относительно границ переменных, пересекаемых данным подконтуром. Контуры могут накладываться друг на друга, т. е. одни и те же квадратики могут входить в несколько контуров. При построении контуров необходимо следить за тем, чтобы не получились такие контуры, все квадратики которых уже вошли в другой контур.
Таким образом, можно организовать три контура (рис. 5. 7). Матрица Карно показывает, можно ли, используя условное состояние, упростить функцию (контуры выделены тонкими линиями).
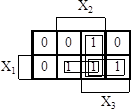
Рисунок 5. 7 – Матрица Карно с выделенными контурами для записи
минимизированной ЛФ
Запишем логическую функцию из матрицы. При записи функции, записываются в неинвертированном состоянии переменные, полностью охватывающие контур, а все переменные, не охватывающие контур – в инвертированном состоянии. Переменные, частично охватывающие контур, вообще не записываются. Таким образом, из матрицы (рис. 5. 7) запишем ЛФ:
| f = X2 X3V X1 X3 V X1 X2 | (5. 5) |
Минимизированную ЛФ следует преобразовать в целях уменьшения числа логических операций (следовательно, и логических элементов).
| f = X2 X3V X1 X3 V X1 X2 = X1 X2 V X3(X1 V X2) | (5. 6) |
Построим схему, реализующую данную функцию. Реализуя выражение (5. 6) получим систему управления (рис. 5. 8), соответствующую заданным условиям работы, но с меньшим количеством элементов.

Рисунок 5. 8 – Структурная схема СУ после минимизации
Общее число элементов может быть доведено до трех, если после реализации X1VX2 подать этот сигнал на вход переключателя X3, на выходе которого получим функцию X3(X1VX2). Схема, реализующая данную функцию, приведена на рис. 5. 9.

Рисунок 5. 9 – Структурная схема СУ после дополнительного преобразования ЛФ
Если требуется построить схему на элементах, реализующих другие виды элементарных функций, то полученные выражения следует преобразовать, используя соотношения и законы алгебры логики, для реализации схемы на элементах «ИЛИ-НЕ-ИЛИ» запишем 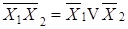 ;
; 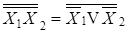 , таким образом, выражение (5. 5) запишем в виде:
, таким образом, выражение (5. 5) запишем в виде:
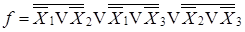
| (5. 7) |
Синтез многотактных САУ.
Синтез многотактных САУ начинается с построения циклограммы. Если циклограмма при этом оказывается нереализуемой, то есть отдельные такты совпадают (имеют одинаковые веса, смысл этого понятия определен ниже), то для различения этих тактов в систему управления вводятся элементы памяти и составляется новая циклограмма. После этого записываются и при необходимости минимизируются логические функции для каждого исполнительного устройства. На основе минимизированных функций строится схема.
Рассмотрим процесс синтеза на примере перекладочного автомата [4]. Структурно-кинематическая схема автомата показана на рисунке 5. 10.
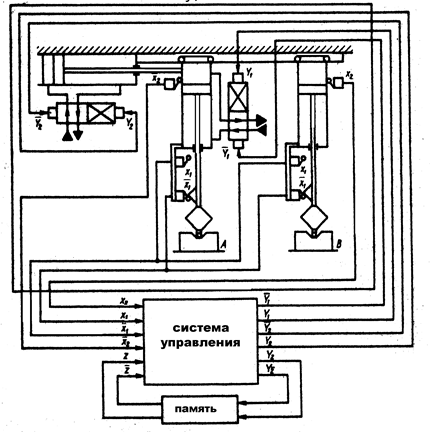
Рисунок 5. 10 – Структурно-кинематическая схема перекладочного автомата
Циклограмма его работы в условных обозначениях имеет вид: 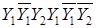 , где Y1 – выдвижение руки захвата;
, где Y1 – выдвижение руки захвата;  – вдвижение руки захвата; Y2 – перенос руки захвата в позицию В;
– вдвижение руки захвата; Y2 – перенос руки захвата в позицию В; 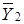 – перенос руки захвата в позицию А. Информация об окончании каждого движения вырабатывается конечными выключателями X1, X2,
– перенос руки захвата в позицию А. Информация об окончании каждого движения вырабатывается конечными выключателями X1, X2, 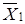 ,
, 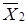 . Циклограмма работы автомата показана на рисунке 5. 11.
. Циклограмма работы автомата показана на рисунке 5. 11.
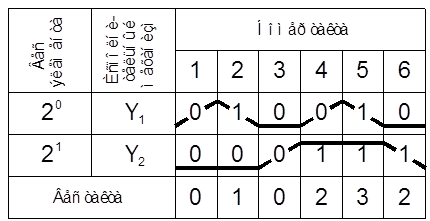
Рисунок 5. 11 – Циклограмма работы перекладочного автомата
Для каждого элемента Y1 и Y2 задан вес в виде соответствующего разряда двоичной комбинации, каждому состоянию каждого элемента присвоено значение «0», если он выключен и включается, или «1», если он включен или выключается. Таким образом, для каждого такта, складывая значения состояний элементов с учетом их весов можно определить веса тактов. Такты 1, 3 и 4, 6 имеют одинаковые веса, то есть циклограмма нереализуема. Для того чтобы сделать ее реализуемой, необходимо ввести элементы памяти. Количество элементов памяти s зависит от числа совпадающих тактов M:
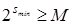 ;
; 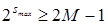 .
.
В рассматриваемом случае M = 2, следовательно, smin = 1, smax = 2. Анализ циклограммы показывает, что достаточно одного элемента памяти, который будет включаться между первым и третьим и выключаться между четвертым и шестым тактами. Полученная реализуемая циклограмма показана на рисунке 5. 12.

Рисунок 5. 12 – Реализуемая циклограмма работы перекладочного автомата
В ней увеличено количество тактов, так как в каждом такте может включаться и выключаться только один элемент.
На основании циклограммы составим таблицу включений (рисунок 5. 13), которая показывает состояние входных и выходных сигналов на каждом такте.
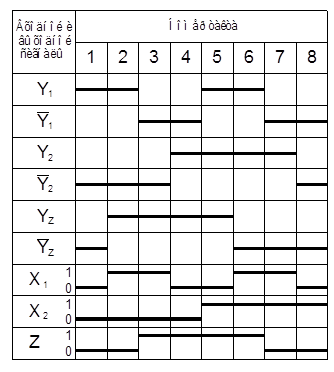
Рисунок 5. 13 – Схема включений перекладочного автомата
В соответствии с циклограммой и таблицей включений составляют логические функции автомата:
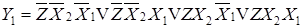 ;
;
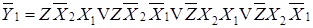 ;
;
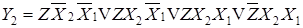 ;
;
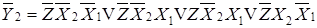 ;
;
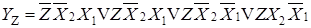 ;
;
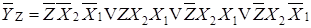 .
.
Элементы схемы, воспринимающие выходные сигналы, могут обладать памятью, как, например, триггеры, распределители гидро- и пневмопотоков и т. д. Именно такие элементы используются в рассматриваемой системе (в качестве элемента памяти используется триггер). Они характеризуются тем, что сохраняют свое состояние до следующей команды на его смену. Поэтому логические функции можно упростить, считая часть комбинаций условными (те комбинации, которые не переводят выходную величину в новое состояние. В следующих формулах эти комбинации взяты в скобки:
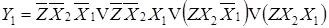 ;
;
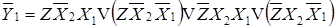 ;
;
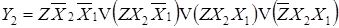 ;
;
 ;
;
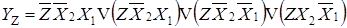 ;
;
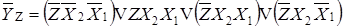 .
.
Эти функции можно минимизировать, используя матрицы Карно (рисунок 5. 14):
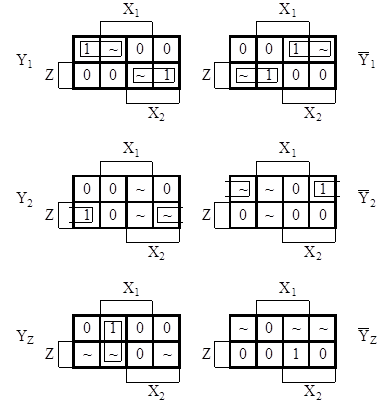
Рисунок 5. 14 – Матрицы Карно для функций управления автоматом-перекладчиком
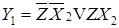 ;
; 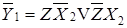 ;
;
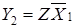 ;
; 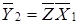 ;
;
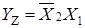 ;
; 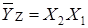 .
.
На основе полученных функций синтезируется система управления (рисунок 5. 15).

Рисунок 5. 15 – Схема управления перекладочным автоматом
|
|
|


