В работе АВИАКОМПАНИИ

Применение метода анализа иерархий

 

Экспертное оценивание - это организация работы со специалистами-экспертами и методы обработки мнений экспер­тов с целью подготовки информации лицами, принимающими решения. Методы экспертного оценивания широко используются при принятии решений в условиях неполной и нечетко сформулиро­ванной информации, в условиях, когда различные обстоятельства, влияющие на выбор, не могут быть выражены в количественной форме, когда для всего многообразия свойств сопоставляемых объектов не удается задать единственный критерий выбора. В по­добных случаях для принятия обоснованных решений приходит­ся опираться на опыт, знания и интуицию специалистов.

Научные основы экспертного оценивания стали широко раз­виваться со второй половины двадцатого столетия, и сегодня это достаточно широкое направление, в рамках которого разработано много теорий, методов и приемов, позволяющих улучшить каче­ство оценивания, а тем самым и обоснованность принимаемых решений.

Так, в «методе комиссий» выработка общих взглядов по об­суждаемой проблеме осуществляется в ходе дискуссий. Однако, возможность влияния аргументов наиболее авторитетного члена комиссии на мнение остальных участников является существен­ным недостатком. В методе «Дельфи» этот недостаток устраняет­ся за счет анонимности экспертизы, а повышение точности экспертной оценки достигается проведением опроса в несколько итераций. Для реализации этого метода требуются значительные затраты времени и финансов.

Для сложных систем обработка экспертных суждений становится столь трудо­емкой, что неизбежно приходится прибегать к помощи компью­терной техники. Сегодня существуют удобные специализирован­ные программы, обеспечивающие, как построение сложных ие­рархических структур в соответствии с методом, так и математи­ческую обработку экспертных суждений, например, Ехреrt Сhoiсе.

Однако, необ­ходимые действия для предварительной оценки можно достаточно просто выполнить и без привлечения компьютера, пользуясь приближенными методами вычисления собственных значений и собственных векторов мат­риц экспертных суждений.

Метод анализа иерархий является системной процедурой для иерархического представления элементов, определяющих со­держание проблемы. Основой метода являются:

- декомпозиция про­блемы на более простые составляющие части;

- дальнейшая обра­ботка суждений на каждом иерархическом уровне с помощью парных сравнений.

Метод анализа включает также процедуры синтеза множественных суждений, определения приоритетности критериев и нахождения альтернативных решений. Реализация метода подлежит проверке и переосмысливанию в случае необходимости до тех пор, пока не будет уверенности, что охвачены все важные для представления и решения проблемы стороны. При этом результаты, полученные на одном из иерархических уровней, используются в качестве входных данных при изучении последующего уровня.

Математический аппарат, применяемый для обработки экспертных суждений

Идеальная схема сравнения объектов

Пусть имеется набор п объектов (факторов), подлежащих сравнению. Обозначим эти объекты символами А₁, А₂,..., А_п.

Пусть в рамках экспертного оценивания эти объекты харак­теризуются соответственно с помощью положительных чисел w₁, w₂,..., w_n на наличие и степень проявления некоторого рассматри­ваемого экспертизой свойства. К примеру, число w_i отражает сте­пень проявления (интенсивность) рассматриваемого свойства у объекта А_i. Числа w_i (i=1,…,n) в зависимости от контекста име­нуют «весами», «интенсивностями», «коэффициентами важно­сти» объектов А_i.

Для удобства, и не в ущерб общности рассматриваемой за­дачи, в дальнейшем будем оперировать нормированными вели­чинами w_i (i=1,…,n), которые обладают тем свойством, что

w₁+ w₂+ w_n=1

Таким образом, при использовании нормированных величин можно утверждать, что w_i ´ 100% представляет собой вес объекта (фактора) А_i выраженный в процентах.

Сопоставим вес каждого из объектов с весами других объек­тов, образуя тем самым так называемую матрицу относительных весов

A=(a_ij)=

Матрица относительных весов обладает четырьмя важными свойствами:

1. a_ij=w_i / w_j > 0 для всех i и j, так как все веса w_i и w_j положительны.

2. a_ij=w_i / w_j=1 для всех i=1, 2,…,n.

3. Матрица А обратно симметрична, а именно a_ij=1/a_ji

a_ij= 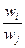= = 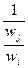для всех i и j.

4. Матрица А обладает свойством совместности, а именно

a_ij´ a_jk= 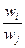´ = =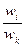a_ik для всех i, j и k.

Если из весов w₁, w₂,…, w_n образовать вектор-столбец w

w= ,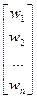

то нетрудно убедиться, что имеет место равенство

A ´ w= n ´ w,

если заметить, что i -я компонента вектора, записанного в левой части соотношения (1), равна

(a_i1 a_{i2 …}a_in) ´ 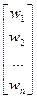= a_i1 ´ w₁ + a_i2 ´ w₂ +…+ a_in ´ w_n=

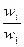= ´ w₁ + 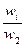´ w₂ +…+ ´ w_n=n´ w_i,

что совпадает с i- й компонентой вектора, расположенного в правой части соотношения.

Выполнение равенства означает, что число n является собственным значением (числом) матрицы относительных весов A в то время как w является собственным вектором, соответствующим этому собственному значению.

Напомним, что в линейной алгебре число l называют собственным значением матрицы A, а ненулевой вектор-столбец x – собственным вектором, соответствующим собственному значению l, если имеет место равенство

A × x = l × x

Собственное значение матрицы A можно найти из так называемого характеристического уравнения

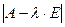= 0,

где 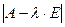- определитель соответствующего матричного выражения, а E –единичная матрица.

Характеристическое уравнение для матрицы n -го порядка представляет собой алгебраическое уравнение n- ой степени. Отсюда следует, что матрица A порядка n, вообще говоря, комплексных собственных чисел, являющихся корнями соответствующего характеристического уравнения.

Для матрицы относительных весов, обладающей четырьмя рассмотренными выше свойствами, можно доказать следующее положение. Матрица относительных весов A=(w_i / w_j) имеет лишь два вещественных собственных значения: n и 0.

Если обозначить l_max = n = max {n;0}, то в соответствии с этой теоремой равенство можно представить в виде

A × w = l_max × w

Равенство является основой для дальнейшей математической обработки и интерпретации экспертных оценок в рамках метода анализа иерархий.

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: