политики авиакомпании в регионе выполнения полетов

Цели	№1	№2	№3	№4	№5	№6	№7	w*	w*норм
№1					1/4		1/7	1,34	0,125
№2	1/5		1/3	1/3	1/6	1/3	1/7	0,29	0,027
№3	1/3				1/4		1/7	0,72	0,067
№4	1/3				1/5		1/7	0,68	0,063
№5								3,58	0,334
№6	1/5		1/3	1/5	1/8		1/8	0,40	0,037
№7					1/2			3,70	0,345
Сумма элементов по столбцам	13,06		16,33	17,83	2,49	27,33	3,69	10,71

 

Как видно из рассматриваемой матрицы, например, фактору №1 эксперты дают сильное превосходство по сравнению с фактором №2, давая оценку 5 баллов. Аналогично определяются и другие парные оценки. Степень превосходства того или иного фактора за­висит от условий реализации проекта в конкретном филиале авиакомпании.

Собственный вектор w^* вычислен по формуле [ ]. В крайней правой колонке таблицы 13 определены компоненты нормированно­го собственного вектора w^* _норм.

Далее следует найти максимальное собственное значение рассматриваемой матрицы. Пользуясь алгоритмом, описанным в [ ], вычислим максимальное собственное значение:

l^*_max ⁼13,06×0,125 + 28×0,027 + 16,33×0,067 + 7,83×0,063 + + 2,49×0,334 + 27,33×0,037 + 3,69×0,345 = 7,71.

Проверяем условие l^*_max ³ п. Условие выполняется, так как 7,71 > 7, где 7 - порядок матрицы.

Вычисляем индекс согласованности.

I_с= 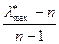= =0,12< 0,2

Таким образом, условие согласованности выполняется.

Следующий этап решения задачи экспертного оценивания состоит в составлении матриц парного сравнения альтернатив А, Б и В реализации политики авиакомпании в регионе выполнения полетов по каждому рассматриваемому фактору. Здесь важно избежать возможную логическую ошиб­ку, которая связана с тем, что на уровне факторов эксперты давали бо­лее высокие оценки наиболее значимым факторам. Поэтому сопоставлять варианты А, Б и В между собой необходимо в том же ключе, т. е. давать более высокие баллы тому варианту, который будет оказывать наиболее сильное влияние по рассматриваемому фактору. Сравним альтернативы А, Б и В для фактора 1.

 

 

Таблица 3

Матрица парных сравнений вариантов реализации политики авиакомпании

для фактора 1

Вариант	А	Б	В	w*	w* норм
А		1/9		0,33	0,099
Б				2,66	0,802
В		1/9		0,33	0,099
Сумма элементов по столбцам		1,22		3,32

l^*_max= 11×0,099 + 1,22×0,802 + 11×0,099 = 3,15 > 3.

I_с = 0,075

 

Таким же образом происходило сравнение по остальным 6-ти факторам.

Итак, все матрицы парных сравнений для уровня альтернатив сформированы. Найдены нормированные собственные векторы, определены собственные значения, подтверждена согласованность матриц.

Теперь необходимо перейти к синтезу окончательного решения. Заключительным шагом здесь является операция взвешивания нормированных собственных векторов альтернатив весами критериев, которые нами были получены в начале решения задачи и содержатся в собственном векторе матрицы критериев.

Обозначим через С матрицу, составленную из нормированных собственных векторов матриц парного сравнения альтернатив.

× =

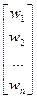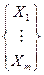
где w - собственный вектор матрицы сравнения критериев,

m – число сравниваемых вариантов (альтернатив),

n – число критериев сравнения,

X₁,…, X_m – вектор приоритетов между вариантами, являющийся окончательным решением задачи.

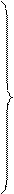В нашем случае:

0,099 0,064 0,235 0,235 0,742 0,069 0,246

0,802 0,185 0,083 0,083 0,062 0,711 0,661 × =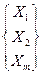

0,099 0,750 0,682 0,682 0,196 0,220 0,093

 

 

где X₁, X₂, X₃ отвечают соответственно вариантам А, Б, В.

Умножая матрицу на вектор-столбец, получаем:

X₁ = 0,099×0,125 + 0,064×0,027 + 0,235×0,067 + 0,235×0,063 + 0,742×0,334 +

0,069×0,037 + 0,246×0,345 = 0,380;

X₂ = 0,802×0,125 + 0,185×0,027 + 0,083×0,067 + 0,083×0,063 + 0,062×0,334 + 0,711×0,037 + 0,661×0,345 = 0434;

X₃ = 0,099×0,125 + 0,750×0,027 + 0,682×0,067 + 0,682×0,063 + 0,196×0,334 +

0,220×0,037 + 0,093×0,345 = 0,216.

 

Итак, =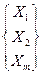

 

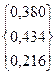
Вариант Б – интенсификация коммерческих усилий (соответствующий элемент вектора X₂) имеет наибольшую оценку (0,434) и, следовательно, является в данной ситуации по согласованному мнению членов Координационного совета авиакомпании наиболее приемлемым.

 

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: