Примеры распределения случайных величин

Способы нахождения значений случайной величины зависят от вида функции ее распределения. Однако на практике такие функции, как правило, неизвестны. Если же случайный характер результатов наблюдений обусловлен погрешностями измерений, то полагают, что наблюдения имеют нормальное распределение. Это обусловлено тем, что погрешности измерений складываются из большого числа небольших возмущений, ни одно из которых не является преобладающим. Согласно же центральной предельной теореме сумма бесконечно большого числа взаимно независимых бесконечно малых случайных величин с любыми распределениями имеет нормальное распределение. Нормальное распределение для

случайной величины х с математическим ожиданием и дисперсией s имеет вид:

Реально даже воздействие ограниченного числа возмущений приводит к нормальному распределению результатов измерений и их погрешностей. В настоящее время наиболее полно разработан математический аппарат именно для случайных величин, имеющих нормальное распределение. Если же предположение о нормальности распределения отвергается, то статистическая обработка наблюдений существенно усложняется и в таком случае невозможно рекомендовать общую методику статистической обработки наблюдений. Часто даже не известно, какая характеристика распределения может служить оценкой истинного значения измеряемой величины.

Выше приведено аналитическое выражение нормального распределения для случайной измеряемой величины х. Переход к нормальному распределению случайных погрешностей осуществляется переносом центра распределений в 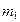и откладывания по оси абсцисс погрешности .

Нормальное распределение характеризуется двумя параметрами: математическим ожиданием m₁ и средним квадратическим отклонением σ.

При многократных измерениях несмещенной, состоятельной и эффективной оценкой m₁ для группы из n наблюдений является среднее арифметическое :

.

Нужно сказать, что среднее арифметическое дает оценку математического ожидания результата наблюдений и может быть оценкой истинного (действительного) значения измеряемой величины только после исключения систематических погрешностей.

Оценка S среднего квадратического отклонения (СКО) дается формулой:

Эта оценка характеризует рассеяние единичных результатов измерений в ряду равноточных измерений одной и той же величины около их среднего значения.

Другими оценками рассеяния результатов в ряду измерений являются размах (разница между наибольшим и наименьшим значением), модуль средней арифметической погрешности (арифметическая сумма погрешностей, деленная на число измерений) и доверительная граница погрешности (подробно рассматривается ниже).

СКО является наиболее удобной характеристикой погрешности в случае ее дальнейшего преобразования. Например, для нескольких некоррелированных слагаемых СКО суммы определяется по формуле:

.

Оценка S характеризует рассеяние единичных результатов наблюдений относительно среднего значения, то есть в случае, если мы за результат измерений примем отдельный исправленный результат наблюдений. Если же в качестве результата измерений принимается среднее арифметическое, то СКО этого среднего определяется по формуле:

Нормальное распределение погрешностей имеет следующие свойства:

1. симметричность, т.е. погрешности, одинаковые по величине, но противоположные по знаку, встречаются одинаково часто;

2. математическое ожидание случайной погрешности равно нулю;

3. малые погрешности более вероятны, чем большие;

_4. чем меньше s, тем меньше рассеяние результатов наблюдений и больше вероятность малых погрешностей.

Другим распространенным в метрологии распределением случайной величины является равномерное распределение - распределение, при котором случайная величина принимает значения в пределах конечного интервала от х₁ до х₂ с постоянной плотностью вероятностей.

Дифференциальная функция равномерного распределения имеет вид:

f(x) = с при х₁ £ x £ х₂

f(x) = 0 при х₂ < x < х₁

При нормировке площади кривой распределения на единицу, получаем, что с(х₂ – х₁) = 1 и с = 1/ (х₂ – х₁).

Равномерное распределение характеризуется математическим ожиданием , дисперсией или СКО _.

Кроме рассмотренных примеров распределений случайных величин существуют и другие важные для практического использования распределения дискретных случайных величин, например, биномиальное распределение и распределение Пуассона. В настоящем курсе они не рассматриваются.

Доверительные интервалы

Приведенные выше оценки параметров распределения случайных величин в виде среднего арифметического для оценки математического ожидания и СКО для оценки дисперсии называются точечными оценками, так как они выражаются одним числом. Однако в некоторых случаях знание точечной оценки является недостаточным. Наиболее корректной и наглядной оценкой случайной погрешности измерений является оценка с помощью доверительных интервалов.

Симметричный интервал в границами ± Δх(Р) называется доверительным интервалом случайной погрешности с доверительной вероятностью Р, если площадь кривой распределения между абсциссами – Δх и + Δх составляет Р -ю часть всей площади под кривой плотности распределения вероятностей. При нормировке всей площади на единицу Р представляет часть этой площади в долях единицы (или в процентах). Другими словами, в интервале от -Dх(Р) до +Dх(Р) с заданной вероятностью Р встречаются Р ×100% всех возможных значений случайной погрешности.

Доверительный интервал для нормального распределения находится по формуле:

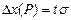
где коэффициент t зависит от доверительной вероятности Р.

Для нормального распределения существуют следующие соотношения между доверительными интервалами и доверительной вероятностью: 1s (Р=0,68), 2s (Р= 0,95), 3s (Р= 0,997), 4s (Р=0,999).

Доверительные вероятности для выражения результатов измерений и погрешностей в различных областях науки и техники принимаются равными. Так, в технических измерениях принята доверительная вероятность 0,95. Лишь для особо точных и ответственных измерений принимают более высокие доверительные вероятности. В метрологии используют, как правило, доверительные вероятности 0,97, в исключительных случаях 0,99. Необходимо отметить, что точность измерений должна соответствовать поставленной измерительной задаче. Излишняя точность ведет к неоправданному расходу средств. Недостаточная точность измерений может привести к принятию по его результатам ошибочных решений с самыми непредсказуемыми последствиями, вплоть до серьезных материальных потерь или катастроф.

При проведении многократных измерений величины х, подчиняющейся нормальному распределению, доверительный интервал может быть построен для любой доверительной вероятности по формуле:

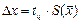
где t_q – коэффициент Стьюдента, зависящий от числа наблюдений n и выбранной доверительной вероятности Р. Он определяется с помощью таблицы q -процентных точек распределения Стьюдента, которая имеет два параметра: k = n – 1 и q = 1 – P; – оценка среднего квадратического отклонения среднего арифметического.

Доверительный интервал для погрешности Dх(Р) позволяет построить доверительный интервал для истинного (действительного) значения измеряемой величины, оценкой которой является среднее арифметическое . Истинное значение измеряемой величины находится с доверительной вероятностью Р внутри интервала: 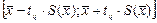. Доверительный интервал позволяет выяснить, насколько может измениться полученная в результате данной серии измерений оценка измеряемой величины при проведении повторной серии измерений в тех же условиях. Необходимо отметить, что доверительные интервалы строят для неслучайных величин, значения которых неизвестны. Такими являются истинное значение измеряемой величины и средние квадратические отклонения. В то же время оценки этих величин, получаемые в результате обработки данных наблюдений, являются случайными величинами.

Недостатком доверительных интервалов при оценке случайных погрешностей является то, что при произвольно выбираемых доверительных вероятностях нельзя суммировать несколько погрешностей, т.к. доверительный интервал суммы не равен сумме доверительных интервалов. Суммируются дисперсии независимых случайных величин: D _å = åD_i. То есть, для возможности суммирования составляющие случайной погрешности должны быть представлены своими СКО, а не предельными или доверительными погрешностями.

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: