Методы обработки результатов прямых измерений

Основные положения методов обработки результатов прямых измерений с многократными наблюдениями определены в ГОСТ 8.207-76.

За результат измерения принимают среднее арифметическое данных n наблюдений, из которых исключены систематические погрешности. При этом предполагается, что результаты наблюдений после исключения из них систематических погрешностей принадлежат нормальному распределению. Для вычисления результата измерения следует из каждого наблюдения исключить систематическую погрешность и получить в итоге исправленный результат i –го наблюдения. Затем вычисляется среднее арифметическое этих исправленных результатов, которое принимается за результат измерения. Среднее арифметическое является состоятельной, несмещенной и эффективной оценкой измеряемой величины при нормальном распределении данных наблюдений.

Следует отметить, что иногда в литературе вместо термина результат наблюдения иногда применяют термин результат отдельного измерения, из которого исключены систематические погрешности. При этом за результат измерения в данной серии из нескольких измерений понимают среднее арифметическое значение. Это не меняет сути излагаемых ниже процедур обработки результатов.

При статистической обработке групп результатов наблюдений следует выполнять следующие операции:

1. Исключить из каждого наблюдения известную систематическую погрешность и получить исправленный результат отдельного наблюдения x.

2. Вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения:

Т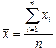

3. Вычислить оценку 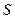среднего квадратического отклонения

группы наблюдений:

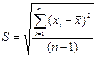
Проверить наличие грубых погрешностей – нет ли значений 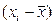, которые выходят за пределы ±3 S. При нормальном законе распределений с вероятностью, практически равной 1 (0,997), ни одно из значений этой разности не должно выйти за указанные пределы. Если они имеются, то следует исключить из рассмотрения соответствующие значения 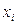и заново повторить вычисления и оценку S.

4. Вычислить оценку СКО результата измерения (среднего

арифметического)

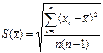
5. Проверить гипотезу о нормальности распределения результатов наблюдений.

Существуют различные приближенные методы проверки нормальности распределения результатов наблюдений. Некоторые из них приведены в ГОСТ 8.207-76. При числе наблюдений меньше 15 в соответствии с этим ГОСТ принадлежность их к нормальному распределению не проверяют. Доверительные границы случайной погрешности определяют лишь в том случае, если заранее известно, что результаты наблюдений принадлежат этому распределению. Приближенно о характере распределения можно судить, построив гистограмму результатов наблюдений. Математические методы проверки нормальности распределения рассматриваются в специальной литературе.

6. Вычислить доверительные границы e случайной погрешности (случайной составляющей погрешности) результата измерения

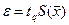
где t_q - коэффициент Стьюдента, зависящий от числа наблюдений и доверительной вероятности. Например, при n = 14, P = 0,95 t_q = 2,16. Значения этого коэффициента приведены в приложении к указанному стандарту.

7. Вычислить границы суммарной неисключенной систематической погрешности (НСП) результата измерений Q (по формулам раздела 4.6).

8. Проанализировать соотношение Q и :

Если 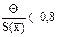, то НСП по сравнению со случайными погрешностями пренебрегают, и граница погрешности результата D = e.. Если 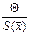> 8, то случайной погрешностью можно пренебречь и граница погрешности результата D = Θ. Если оба неравенства не выполняются, то границу погрешности результата находят путем построения композиции распределений случайных погрешностей и НСП по формуле: 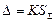, где К – коэффициент, зависящий от соотношения случайной погрешности и НСП; S_å - оценка суммарного СКО результата измерения. Оценку суммарного СКО вычисляют по формуле:

.

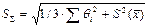Коэффициент К вычисляют по эмпирической формуле:

.

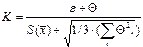Доверительная вероятность для вычисления и 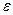должна быть одной и той же.

Погрешность от применения последней формулы для композиции равномерного (для НСП) и нормального (для случайной погрешности) распределений достигает 12 % при доверительной вероятности 0,99.

9. Записать результат измерений. Написание результата измерений предусмотрено в двух вариантах, так как следует различать измерения, когда получение значения измеряемой величины является конечной целью, и измерения, результаты которых будут использоваться для дальнейших вычислений или анализа.

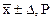В первом случае достаточно знать общую погрешность результата измерения и при симметричной доверительной погрешности результаты измерений представляют в форме:, где

где – результат измерения.

Во втором случае должны быть известны характеристики составляющих погрешности измерения – оценка среднего квадратического отклонения результата измерения , границы НСП , число выполненных наблюдений 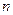. При отсутствии данных о виде функций распределения составляющих погрешности результата и необходимости дальнейшей обработки результатов или анализа погрешностей, результаты измерений представляют в форме:

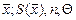
Если границы НСП вычислены в соответствии с п.4.6, то дополнительно указывают доверительную вероятность Р.

Оценки , и производные от их величины могут быть выражены как в абсолютной форме, то есть в единицах измеряемой величины, так и относительной, то есть как отношение абсолютного значения данной величины к результату измерения. При этом вычисления по формулам настоящего раздела следует проводить с использованием величин, выраженных только в абсолютной или в относительной форме.

 

Однократные измерения

В технике большинство измерений являются однократными, т.е. для получения результата измерения используется одно показание прибора. К такому виду относятся, например, измерения при проведении индивидуального дозиметрического контроля, при которых часто используется один детектор. Результат однократного измерения включает в себя все присущие ему погрешности (инструментальную, методическую, субъективную), в каждой из которых могут быть как систематические, так и случайные составляющие. Если при этом необходимо точно оценить погрешность результата измерений, то следует выявить и оценить все составляющие погрешностей и просуммировать их.

Случайная составляющая погрешности не может быть рассчитана по результатам измерения, хотя она неявно присутствует в нем. В качестве оценки случайной составляющей погрешности может быть использован, например, коэффициент вариации, определяемый предварительно в процессе многократных измерений при изучении воспроизводимости показаний данного прибора. Коэффициент вариации находится как отношение оценки среднего квадратического отклонения к среднему арифметическому показаний прибора при многократных измерениях. В некоторых случаях случайная погрешность может определяться доверительными границами.

Оценку систематических погрешностей можно получить по характеристикам используемого прибора (по паспортным данным или из свидетельства о поверке) и метода измерения (путем его анализа). Из документации на прибор можно оценить и учесть дополнительные систематические погрешности.

Основные этапы оценки погрешности при однократных измерениях с точным оцениванием погрешности следующие:

1. Учитывается систематическая погрешность прибора.

2. Оценивается систематическая погрешность метода измерений.

3. Оцениваются по документации на прибор дополнительные систематические погрешности, обусловленные влияющими величинами.

4. Из отсчета прибора исключаются все известные систематические погрешности (в соответствии с пп. 1, 2, 3) и определяется исправленный результат измерения, который содержит НСП и случайные составляющие погрешности.

5. Оцениваются границы Q_i составляющих НСП, распределение которых принимается равномерным. Ими могут быть, например, погрешности эталонов при поверке СИ, погрешности поправок и т.п. После этого определяются границы Q суммарной НСП по приведенным выше формулам.

6. Предварительно перед использованием прибора определяется коэффициент вариации - оценка случайной погрешности, которая используется при последующих однократных измерениях с прибором.

7. Сопоставляются оценки НСП и случайной погрешности по критериям предыдущего раздела и при возможности пренебрежения какой-либо из них определяются границы погрешности результата D.

Если необходимо учитывать обе составляющие, то в качестве границы погрешности результата измерения D принимается суммарная средняя квадратическая погрешность S_å,, вычисляемая по формуле раздела 4.7 с определением СКО результата измерений и полуэмпирического коэффициента К. Для исключения грубых погрешностей однократное измерение следует повторять 2-3 раза и за результат принимать среднее арифметическое.

На практике часто встречаются измерения, для которых нет необходимости точно оценивать погрешность. В таких измерениях в качестве результата принимают значение отсчета х, а для оценивания погрешности измерения используются предел допускаемой основной погрешности прибора D_пр и дополнительные погрешности прибора Y_i от влияющих величин. Субъективные погрешности при этом считаются малыми и ими пренебрегают.

Оценка погрешности результата измерения D_å определяется как сумма абсолютных величин основной погрешности и суммарной систематической по формуле:

D_å = |D_пр| + å|Y_i|.

Более точная оценка погрешности может быть получена статистическим сложением составляющих по формуле раздела 4.7 в предположении их равномерного распределения.

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: