Главная | Обратная связь | Поможем написать вашу работу!

Задания для контрольной работы № 2

№ вари-анта	Две последние цифры шифра учащегося	Номера задач	№ вари-анта	Две последние цифры шифра учащегося	Номера задач
	01 51	1,7,13,19,21,30		26 76	4,6,14,19,22,26
	02 52	3,6,14,20,22,28		27 77	5,6,13,18,24,29
	03 53	5,8,15,16,25,29		28 78	4,8,14,20,25,26
	04 54	2,9,11,17,24,27		29 79	4,7,11,17,23,28
	05 55	4,10,12,18,23,26		30 80	1,6,12,18,23,27
	06 56	2, 7,14,20,22,29		31 81	4,9,13,19,23,26
	07 57	4,6,15,16,21,28		32 82	2,10,15,16,22,30
	08 58	1,8,11,17,24,30		33 83	1,8,13,18,21,29
	09 59	3,9,12,18,23,27		34 84	2,10,14,19,24,26
	10 60	1,6,11,16,25,26		35 85	3,10,14,18,25,29
	11 61	2,7,11,16,22,26		36 86	4,7,15,20,24,26
	12 62	3,8,12,16,21,27		37 87	5,7,14,19,22,29
	13 63	4,9,12,17,23,28		38 88	1,9,15,16,21,30
	14 64	5,10,12,17,25,30		39 89	5,7,12,18,23,27
	15 65	3,9,15,20,21,29		40 90	3,8,13,19,21,28
	16 66	2,8,15,17,22,30		41 91	5,9,14,20,22,26
	17 67	4,10,15,19,25,27		42 92	3,10,11,17,24,30
	18 68	1,6,13,17,23,29		43 93	1,9,14,19,25,28
	19 69	3,7,15,16,24,28		44 94	2,6,15,20,23,29
	20 70	5,6,14,17,21,26		45 95	3,6,15,19,21,26
	21 71	2,8,12,18,21,27		46 96	4,8,11,16,23,30
	22 72	1,10,14,20,23,30		47 97	5,9,11,16,24,27
	23 73	1,7,12,17,23,29		48 98	5,10,13,19,23,29
	24 74	2,9,13,18,22,27		49 99	3,7,11,20,25,30
	25 75	3,9,13,17,25,28		50 00	2,6,13,19,22,28

Задача 1.

На рис.1 изображен магиитопровод с воздушным зазором. Материалом сердечника - электротехническая сталь. Размеры сердечника по средней магнитной линии в мм: , , , 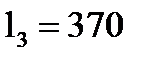. Толщина сердечника 50мм. В сердечнике требуется создать магнитный поток Ф = 0,0048Вб.

Определить ток, который должен проходить по обмотке катушки, если она имеет w = 800 витков. Вычислить также ток катушки для создания заданного магнитного потока, если в сердечнике будет отсутствовать воздушный зазор. Кривая намагничивания приведена на рис.7.

Рис.1

Задача 2.

Магиитопровод выполнен из электротехнической стали и имеет два воздушных зазора (рис.2). Размеры магнитопровода по средней магнитной линии в мм: , , , . Толщина сердечника 50 мм.

Требуется в стержне, на котором расположена обмотка, создать магнитную индукцию В₂ = 1,2Т. определить ток, который необходимо пропустить по обмотке, чтобы создать заданную магнитную индукцию, если обмотка имеет ω= 200 витков.

Кривая намагничивания приведена на рис. 7

Задача 3.

Магиитопровод выполнен из электротехнической стали (рис.3) и имеет воздушный зазор. Размеры сердечника по средней магнитной линии в мм: l₁ = 320, 1₂ = 250,1₃ = 490,1₀ = 1,5. Толщина сердечника 50мм.

Определить число витков катушки со, необходимое для создания в магнитопроводе магнитного потока , если по катушке будет проходить ток 1=5 А.

Какое число витков катушки потребуется при тех же условиях, если в сердечнике будет отсутствовать воздушный зазор? Кривая намагничивания приведена на рис. 7.

Задача 4.

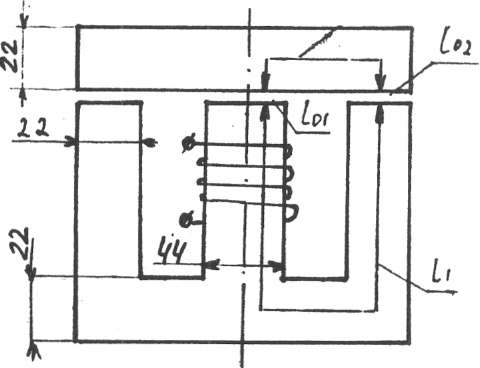
В воздушном зазоре крайнего стержня магнитопровода (рис.4) необходимо создать магнитную индукцию В=1,2 Тл. Катушка, расположенная на среднем стержне, имеет w=400витков. Магиитопровод изготовлен из электротехнической стали. Размеры сердечнбика по средней магнитной линии в мм: 1₁ = 250, 1₂ = 75, 1₀₁ = 1₀₂= 2. Толщина сердечника 40 мм.

Вычислить магнитный поток в среднем стержне. Определить ток катушки, необходимый для создания заданной магнитной индукции. Какой ток катушки потребуется, если при тех же условиях в сердечнике будут отсутствовать воздушные зазоры?

Кривая намагничивания приведена на рис.7.

Задача 5.

Катушка, которая имеет w =300 витков, намотана на прямоугольном сердечнике квадратного сечения, одинакового по всей длине (рис.5). Сердечник выполнен из электротехнической стали. Размеры сердечника: 1=160мм; Ь=22омм; с=50мм. По катушке проходит ток I=2А.

Определить магнитный поток Ф, который создается в сердечнике катушки. Потоком рассеяния пренебречь.

Определить, какой величины возникает магнитный поток Ф от той же катушки с током I=2А, если увеличится высота сердечника до Ь=400мм, ширина до 1=3 00мм при неизменной площади поперечного сечения.

Кривая намагничивания приведена на рис.7.

Рис.5

Задача 6.

Конденсатор емкостью С=159 мкФ соединен последовательно с резистором R=150m. Цепь подключена к напряжению U=225B частотой f=50 Гц.

Начертить схему цепи. Определить сопротивление конденсатора х_с, полное сопротивление цепи z, коэффициент мощности cos ср, ток в цепи I, падения напряжения Ua и Uc на активном и емкостном сопротивлениях.

Построить в масштабе m_u = 30 (В/см) векторную диаграмму напряжений, отложив горизонтальный вектор тока.

Задача 7.

К переменному напряжению U = 150В частотой f= 50 Гц подключены последовательно соединенные резистор и конденсатор. По цепи проходит ток I=3А, при этом на резисторе возникает падения напряжения Uа=90В.

Начертить схему цепи. Определить полное сопротивление цепи z, сопротивление резистора R, сопротивление хс и емкость С конденсатора, коэффициент мощности cosφ, напряжения Uc на емкостном сопротивлении.

Построить в масштабе mu= 20 (В/см) векторную диаграмму напряжений, отложив горизонтально вектор тока.

Задача 8.

Последовательно соединены резисторы сопротивлением R = 90Ом, и конденсатор, имеющий сопротивление хс = 120Ом. По цепи походит ток I=2А.Частотанапряжения питающей сети f = 50Гц.

Начертить схему цепи. Определить полное сопротивление цепи z, коэффициент мощности cosφ, подведенное напряжение U, падения напряжения Ua и Uc на активном и емкостном сопротивлениях, емкость конденсатора С.

Построить в масштабе mu = 40 (В/см) векторную диаграмму напряжений, отложив горизонтально вектор тока.

Задача 9.

Последовательно соединены резистор и конденсатор. Цепь подключена к переменному напряжению частотой f = 50 Гц. Известны падения напряжения на активном Uа=120в и емкости Uc=60Ом.

Начертить схему цепи. Определить на зажимах цепи U, ток в цепи I, емкостное сопротивление хс и емкость С конденсатора, полное сопротивление цепи z, коэффициент мощности cosφ.

Построить в масштабе mc =20(В/см) векторную диаграмму напряжений, отложив горизонтально вектор тока.

Задача 10.

Последовательно соединены конденсатор емкостью С = 198,5 мкФ и резистор, имеющий сопротивление R=12 Ом. По цепи проходит ток I=7,5 А с частотой f=50 Гц.

Начертить схему цепи. Определить схему конденсатора хс, полное сопротивление цепи z, коэффициент мощности cos φ, подведенное напряжение U, падения напряжения на активном Ua и емкостном Uс сопротивлениях.

Построить в масштабе mu = 20 (В/см) векторную диаграмму напряжений, отложив горизонтально вектор тока.

Задача 11.

В сеть переменного тока напряжением U = 200В и частотой f=50 Гц включены последовательно катушка с активным сопротивлением R= 16 Ом и индуктивным хL = 12 Ом и конденсатор, сопротивление которого хс = 42 Ом.

Начертить схему цепи. Определить полное сопротивление цепи z; ток катушки L и емкость конденсатора С.

Определить частоту f0, при которой наступит резонанс напряжений.

Для режима резонанса напряжений определить индуктивное X_L₀, емкостное X_C₀ полное Z сопротивление цепи; ток I₀; падение напряжения на индуктивном ULo и емкостном Uco сопротивлениях; коэффициент мощности цепи cos φ, полную S, активную Р и реактивную Q мощности цепи.

Для режима резонанса построить в масштабе mu = 50 (В/см) векторную диаграмму напряжений, отложив горизонтально вектор тока.

Задача 12.

Катушка, имеющая активное сопротивление R=5Ом и индуктивность L = 0,0383 Г, соединена последовательно с конденсатором, емкость которого С=265 мкФ. Цепь подключена к сети переменного тока напряжением U=120В и частотой f=50 Гц.

Начертить схему цепи. Определить емкостное X_C, индуктивное X_L и полное Z сопротивление цепи; ток I; падение напряжения на активном UL и емкостном Uc сопротивлениях; коэффициент мощности цепи cos φ, полную S, активную Р и реактивную Q мощности цепи.

Определить полное сопротивление цепи z1 и ток I1; падения напряжения на активном U a1, индуктивном U L1, емкостном Uc1 сопротивлениях и коэффициент мощности цепи cos φ1, если частота питающего напряжения повысится до f1 = 100Гц.

Задача 13.

Последовательно с катушкой, активное сопротивления которой R=5 Ом индуктивное XL= 260м, включен конденсатор, емкостное сопротивление которого Xс = 14 Ом. Ток в цепи I = 12А, частота f = 50Гц.

Начертить схему цепи. Определить полное сопротивление цепи z; коэффициент мощности cos φ и напряжение на зажимах цепи U.

Вычислить индуктивность катушки Lо, при которой в цепи наступит резонанс напряжений. Для режима резонанса напряжений определить полное сопротивление цепи Z0; ток l0; падения напряжения на активном URo и емкостном Uco сопротивлениях; коэффициент мощности цепи cos φ, полную S, активную Р и реактивную Q мощности цепи.

Построить в масштабе mu= 50 (В/см)векторную диаграмму напряжений для режима резонанса, отложив горизонтально вектор тока.

Задача 14.

В сеть переменного ток напряжением U=220В и частотой f=50 Гц последовательно включены катушка с активным сопротивлением R = 16 Ом и индуктивным XL= 70м и конденсатор, сопротивление которого Xс = 190м.

Начертить схему цепи. Определить полное сопротивление цепи z; ток I; падения напряжения на активном Uа, индуктивном UL и емкостном Uc сопротивлениях; коэффициент мощности цепи cos φ.

Построить в масштабе mu = 50 (В/см) векторную диаграмму напряжений, отложив горизонтально вектор тока.

Вычислить емкость конденсатора Со, при которой в данной цепи наступит резонанс напряжений. Для режима резонанса напряжений определить сопротивление цепи Z0; ток I0; коэффициент мощности cos φ0, полную S, активную Р и реактивную Q мощности цепи.

Задача 15.

В сеть переменного тока напряжением U = 200В и частотой f=50Гц последовательно включены конденсатор, сопротивление которого XC = 90Ом, и катушка с активным сопротивлением R = 40Ом и индуктивным XL = 90 Ом.

Начертить схему цепи. Определить полное сопротивление цепи z; ток I; падение напряжения на активном Uа, индуктивном UL и емкостном Uc сопротивлениях; коэффициент мощности цепи cos φ, полную S, активную Р и реактивную Q мощности цепи.

Построить в масштабе mu= 50 (В/см) векторную диаграмму напряжений, отложив горизонтально вектор тока.

Определить полное сопротивление z1; ток I1; и коэффициент мощности cos φ₁ и реактивную мощность Q1 цепи, если частота питающего напряжения увеличится в 1,5 раза.

Задача 16.

В сеть переменного тока напряжением U = 220 и частотой f=50 Гц параллельно включены две катушки. Первая катушка имеет активное сопротивление R1 = 20 Ом и индуктивное XL1= 150м. Вторая катушка имеет активное сопротивление R2 = 160м индуктивное XL2= 30 Ом.

Начертить схему цепи. Определить ток катушек I1; I2; ток I в неразветвленной части цепи; коэффициент мощности cos φ и активную мощность Р всей цепи.

Задачу решить методом разложения токов на активные и реактивные составляющие.

Построить в масштабе mI = 2 А/см векторную диаграмму токов, отложив горизонтально вектор напряжения.

Вычислить емкость Со конденсатора, который следует включить параллельно катушкам, чтобы в цепи возник резонанс токов.

В режиме резонанса определить ток Iо в неразветвленной части цепи.

Задача 17.

В сети переменного тока напряжением U=220 В включены параллельно два приемника энергии. Первый приемник состоит из последовательно соединенных активного R1 = 5Ом и индуктивного X_L₁= 12 Ом сопротивлений; второй – из последовательно соединенных активного R2 = 12Ом и емкостного Xс = 16Ом сопротивлений.

Начертить схему цепи. Определить ток катушек I1; I2; ток I в неразветвленной части цепи; коэффициент мощности cos φ всей цепи, активную мощность Р, реактивную Q и полную S мощности всей цепи.

Задачу решить методом разложения токов на активные и реактивные составляющие.

Построить в масштабе m1 = 2 А/см векторную диаграмму токов, отложив горизонтально вектор напряжения. Вычислить активную g реактивную bL проводимости первого приемника.

Задача 18

В сеть переменного тока напряжением U=380 В и частотой f =50 Гц включены параллельно два источника энергии: первый мощностью Р₁ = 10 кВт с соsφ₁ = 1; второй мощностью Р₂= 6,6 кВт с соs φ₂ = 0,5 (индуктивный).

Начертите схему цепи. Определить ток катушек I₁, I₂; ток I в неразветвленной части цепи; активную Р, реактивную Q и полную S мощности всей цепи.

Задачу решить методом разложения токов на активные и реактивные составляющие.

Построить в масштабе m₁ = 2 А/см векторную диаграмму токов, отложив горизонтально вектор напряжения.

Вычислить емкость Со конденсатора, который следует включить параллельно приемникам, чтобы в цепи возник резонанс токов.

Определить для режима резонанса ток Iо в неразветвленной части цепи и соs φ₀ всей установки.

Задача 19

Цепь переменного тока состоит из двух параллельных ветвей. В первую ветвь включены последовательно активное и индуктивное сопротивления: R₁ = 12 Ом; X_L= 9 Ом. Вторая ветвь состоит из последовательно соединенных активного и емкостного сопротивлений: R₂ = 12 Ом; X_C = 16 Ом. Напряжение на зажимах цепи U=220 В. Начертить схему цепи. Определить ток катушек I₁, I₂; ток I в неразветвленной части цепи; коэффициент мощности соs φ всей цепи, активную Р, реактивную Q и полную S мощности всей цепи.

Задачу решить методом разложения токов на активные и реактивные составляющие.

Построить в масштабе m₁ = 2 А/см векторную диаграмму токов, отложив горизонтально вектор напряжения.

Вычислить активную g и реактивную b_C проводимость второй ветви.

Задача 20

В сеть переменного тока включены параллельно два приемника энергии. Первый приемник представляет собой катушку мощностью Р₁ = 7,2 кВт с соsφ₁ = 0,5. Второй приемник состоит из последовательно соединенных активного R₂ = 30 Ом и емкостного X_C = 16 Ом сопротивлений. Ток второго приемника I₂ = 17,6 А.

Начертить схему цепи. Определить напряжение U на зажимах цепи; ток I₁ первого приемника; ток I в неразветвленной части цепи; коэффициент мощности соs φ всей цепи, активную Р, реактивную Q и полную S мощности всей цепи.

Задачу решить методом разложения токов на активные и реактивные составляющие.

Построить в масштабе m₁ = 2 А/см векторную диаграмму токов, отложив горизонтально вектор напряжения. Вычислить активную g и реактивную b_C проводимость второго приемника.

Задача 21

Три одинаковых приемника с сопротивлениями Z_A = Z_B = Z_С = (12+j16) Ом соединены звездой и питаются от трехфазной сети с линейным напряжением U_Л = 220 В.

Начертить схему цепи. Определить фазное напряжение U_Ф: фазные I_Ф и линейные I_Л токи; полную S, активную Р и реактивную Q мощности и коэффициент мощности соs φ трехфазного потребителя.

Построить в масштабе m_u = 40 В/см, m₁= 2 А/см векторную диаграмму напряжения и токов.

Задача 22

В трехфазную сеть напряжением U_Л = 380 В звездой включен приемник энергии мощностью Р = 6 кВт с коэффициентом мощности соs φ = 0,85 (индуктивный).

Начертить схему цепи. Определить фазное напряжение U_Ф; фазный I_Ф и линейный I_Л токи; полное сопротивление фазы Z_Ф; полную S, активную Р и реактивную Q мощности трехфазного потребителя.

Построить в масштабе m_u = 50 В/см, m₁= 5 А/см векторную диаграмму напряжения и токов.

Задача 23

В трехфазную четырехпроводную сеть напряжением U_Л = 380 В звездой включены три группы ламп накаливания. Сопротивление каждой лампы R_Л = 440 Ом. Число ламп в каждой фазе n_А = 20; n_В = 30, n_С =40; лампы в фазах соединены параллельно. Начертить схему цепи. Определить фазное напряжение U_Ф, фазные сопротивления R_А, R_В, R_С; фазные I_Ф и I_Л токи; активную мощность Р всех трех фаз.

Построить в масштабе m_u = 50 В/см, m₁= 5 А/см векторную диаграмму напряжения и токов; графически (из векторной диаграммы) определить ток в нейтральном (нулевом) проводе I_о.

Задача 24

В трехфазную четырехпроводную сеть напряжением U_Л = 380 В звездой включены приемники энергии. Мощность приемников в фазе А - Р_А = 1,5 кВт, в фазе В - Р_В = 2 кВт, в фазе С - Р_С = 1,0 кВт. Для всех приемников соs φ = 1.

Начертить схему цепи. Определить фазное напряжение U_Ф; фазные I_Ф и линейные I_Л токи; активную мощность трех фаз.

Задача 25

В трехфазную сеть напряжением U_Л = 220 В включен двигатель, потребляющий мощность Р = 9 кВт. Обмотка двигателя соединена звездой. Линейный ток двигателя I_Л= 50 А.

Начертить схему цепи. Определить фазное напряжение U_Ф; полное Z_Ф, активное R_Ф и индуктивное х_L_Фсопротивления фазы; коэффициент мощности соs φ, полную S и реактивную Q мощности двигателя.

Построить в масштабе m_u = 40 В/см, m₁= 20 А/см векторную диаграмму напряжения и токов.

Задача 26

Конденсатор емкостью С = 1 мкФ, соединенный последовательно с резистором, сопротивление которого R = 5 МОм, заряжается от сети с постоянным напряжением U = 100 В.

Начертить схему цепи. Определить постоянную времени цепи τ и значение зарядного тока и напряжения на обкладках конденсатора для момента времени t = 0; τ; 2 τ; 3 τ; 4 τ; 5 τ.

Построить в масштабе кривые u_с = f (t) и i_зар = f₁ (t).

Задача 27

Конденсатор емкостью С = 5 мкФ, заряженный предварительно до напряжения U = 110 В, разряжается через резистор, сопротивление которого R = 5 МОм.

Начертить схему цепи. Определить постоянную времени цепи τ и значение разрядного тока и напряжения на обкладках конденсатора для момента времени t = 0; τ; 2 τ; 3 τ; 4 τ; 5 τ.

Построить в масштабе кривые u_с = f (t) и i_разр = f₁ (t).

Задача 28

Катушка с активным сопротивлением R = 10 Ом и индуктивностью L = 0,2 Г замыкается накоротко. Ток в катушке до короткого замыкания был равен I_о = 20 А.

Начертить схему цепи. Определить постоянную времени цепи τ и значение тока переходного процесса для моментов времени t = 0; τ; 2 τ; 3 τ; 4 τ; 5 τ.

Построить в масштабе кривую i_кз = f (t).

Задача 29

Катушка с активным сопротивлением R = 6 Ом и индуктивностью L = 0,3 Г включается в сеть с постоянным напряжением U =60 В.

Начертить схему цепи. Определить постоянную времени цепи τ и значение тока в катушке для моментов времени t = 0; τ; 2 τ; 3 τ; 4 τ; 5 τ.

Построить в масштабе кривую i = f (t).

Задача 30

Конденсатор емкостью С = 30 мкФ, соединены последовательно с резистором, сопротивление которого R =0,5 МОм, заряжается от сети с постоянным напряжением U=220 В.

Определить постоянную времени цепи τ и значение зарядного тока и напряжения в конденсаторе для момента времени t = 0; τ; 2 τ; 3 τ; 4 τ; 5 τ.

Начертить схему цепи. Построить в масштабе кривые и i_разр = f₁ (t), u_с = f₁ (t)

Кривая намагничивания электротехнической стали

Методические указания

к выполнению домашней контрольной работы №2

Приступая к расчету магнитной цепи, следует разделить на участки. Каждый из которых должен иметь по всей длине одинаковое сечение и одинаковый материал. За длины участков принимаются соответствующие длины средней магнитной линии.

Пример 1.

В среднем воздушном зазоре магнитопровода необходимо создать магнитный поток 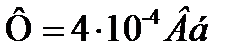. Катушка расположенная на среднем стержне, имеет w =300 витков (рис. 6)

Магнитопровод изготовлен из электротехнической стали. Размеры магнитопровода указаны в мм. Определить ток в катушке.

Решение.

Данная магнитная цепь является разветвленной и симметричной. Разделим ее по оси симметрии 0-0 на две половины. Расчет будем вести для одной половины сердечника. Полными словами, после разделения получена неразветвленная магнитная цепь, во всех сечениях которой магнитный поток одинаков и равен половине потока, проходящего в среднем стержне, т.е.

Ф₁ =Ф/2=4 10 ^-4/2 = 2 10^-4 Вб

Разобьем теперь магнитную цепь на участки. По всей длине расчетная половина магнитопровода имеет одинаковую площадь поперечного сечения. Однако, из-за неоднородности материала магнитопровода (сталь и воздух) его надо делить на два участка.

По средней магнитной линии определяем длины участка, длина участка из электрической стали.

1 ст = (40-10)2 + (70-10)2 = 180мм = 18см;

Длина воздушного зазора

1 о = 1+1=2мм = 0,2 см.

Поперечное сечение обоих участков одинаково

S= 20 10 =200 мм² = 2 10^-4 м²

Величина магнитных индукций обоих участков одинакова, т.к. участки имеют одинаковое сечение и по ним проходит один и тот же магнитный поток, следовательно

Вст = Во= Oj/S =2 10^-4 /2 10^-4= 1Т.

По кривой намагничивания находим напряженность магнитного поля для участка из электротехнической стали.

Нст= 3,5 А/см.

Напряженность магнитного поля для воздушного зазора находится по формуле

Но=0,8Во 10 ⁴= 0,810 ⁴ =8000 А/см

где Во-магнитная индукция в теслах.

По закону полного тока определяем намагничивающую силу

∑Iw = ∑Hl

Iw = Нст lст + Но lо = 3,5 18 + 8000 0,2 = 1663 А.

Определяем ток в катушке I = Iw / w = 1663/300=5,5А.

В задаче 5 требуется по заданным току I и числу витков в катушке w определить магнитный поток в сердечнике без зазора. В этом случае по закону полного тока (∑Iw = ∑Hl) следует определить напряженность магнитного поля. Затем по кривой намагничивания для материала сердечника находится значение магнитной индукции В. Зная В и размеры сердечника, нетрудно определить магнитный поток.

Задачи 6-10 посвящены расчету цепей переменного тока с последовательным соединением активного сопротивления R и индуктивного х_L; активного сопротивления R и емкостного х_с.

К расчету таких цепей можно приступить только после изучения свойств простейших цепей переменного тока, к которым относятся цепи:

А)с сопротивлением R;

Б) с индуктивностью L;

А)с емкостью С.

В таблице приводятся свойства этих цепей.

Пример 2.

К источнику переменного тока с напряжением u=310 sin(314t - π/3) В подключены последовательно резистор с сопротивлением R и конденсатор емкостью С (рис.8). ток в цепи выражается уравнением: І = 7,05 sin314t А. Определить сопротивление резистора R емкость конденсатора С; коэффициент мощности цепи cos ф; активную Р, реактивную Q и полную S мощности.

Построить в масштабе векторную диаграмму напряжений, отложив горизонтально вектор тока.

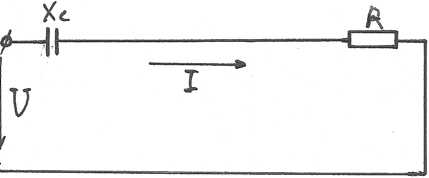
Рис. 8

Решение

Действующее значение напряжения и тока U= = 310/1,41=220В;

І = =7,05/1,41 =5 А.

Полное сопротивление цепи Z=U/I=220/5=44 Ом.

Угол сдвига между током и напряжением по условию Ф=18073=60°, т.е. напряжение отстает от тока на угол ф=60° (cos ф= cos60° = 0,5).

Сопротивление резистора R=Z*cosф =44*0,5 =22 Ом.

Емкостное сопротивление конденсатора

или х_с = z*sinф=44*0,866 =380м

Угловая частота по условию равна 314рад/с; следовательно, f=w/2π=314/6,28=50 Гц.

Емкость конденсатора

Активная мощность цепи P=UI cos ф= 220 5 0,5 =550 Вт.

Реактивная мощность цепи

Q=U I sinф = 220 5 0,866 = 950 вар.

Полная мощность цепи

S=U I =220 5 = 1100 BA.

Для построения векторной диаграммы вычислим составляющие напряжения:

Активную Ua=I R =5 22= 110В;

Реактивную Uc= I х_с = 5 38 = 190 В.

Векторная диаграмм построена на рис.9 в масштабе m_u= 40 В/см.

Длины векторов напряжений:

Lu= U/ m_u = 220/40 =5,5 см;

Lua=Ua/ m_u =110/40 =2,75 см;

Luc=Uc/ m_u =190/40=4,75 см.

За исходный вектор принимаем вектор тока и откладываем его по оси абсцисс.

Вектор активного напряжения Ua совпадает по фазе с током, а вектор емкостного напряжения Uc отстает от тока на 90°.

Вектор приложенного напряжения равен геометрической сумме Ua и Uc, т.е. U=Ua+Uc.

Задачи 11-15 посвящены расчету цепей переменного тока с последовательным соединением активного, индуктивного и емкостного сопротивлений. При равенстве реактивных сопротивлений X_L = Хс в такой цепи возникает резонанс напряжений.

Пример 3

В сеть переменного тока напряжением U = 220В и частотой f = 50Гц включены последовательно катушка с активным сопротивлением R=8 Ом и индуктивностью L=102 мГ, и конденсатор емкостью С=523 мкФ (рис. 10) Вычислить ток в цепи. Построить в масштабе векторную диаграмму напряжений, отложив горизонтально вектор тока.

Определить частоту переменного тока f₀, при которой в цепи наступит резонанс напряжений. Вычислить ток в цепи и напряжение на конденсаторе при резонансе.

Решение.

Реактивные сопротивления катушки и конденсатора

X_L = 2πfL = 314* 102 • 10 ^_3 = 32 Ом

Х_с = l/(2πfC) =10⁶/ 314* 523 = 6,1 Ом

Полное сопротивление цепи

Z= V R²+ (X_l- X _с) ² = л/8² + (32 - 6,1)² = 27,1 Ом.

Ток в цепи по закону Ома I = U / z = 220 / 27.1 = 8.1 А

Для построения векторной диаграммы вычислим составляющие напряжения:

Активную U_a = I- R=8.1 - 8 = 64.8 В Индуктивную U _L = I • X_L= 8.1 • 32 = 258 В Емкостную Uc⁼I'X_c=8,l -6,1= 49,4 В.

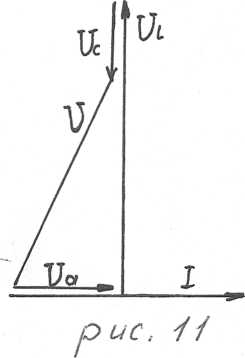
Векторная диаграмма построена на рис. 11 в масштабе m _u = 40 В /см

Длины векторов напряжения:

Активного Lua = Ua/m_u = 64,8 /40 =1,62 см Индуктивного L _uL =U_L/m _u = 258 / 40 = 6,45 см Емкостного L_uc = U с /т _u = 49,4 /40 = 1,23 см Приложенного L_u = U/ m_u = 220 / 40 = 5,5 см

Поскольку X_L > X с, то приложенное напряжение опережает ток в цепи, т.е. угол ср положительный.

Частота переменного тока, при которой в цепи наступает резонанс

напряжений:

f₀= 1 /2π VLC= 1/6,28 V 102*10-³ • 523*10-⁶=21,8Гц/

Ток при резонансе 1₀= U/R = 220/8 = 27,5 А

Реактивное сопротивление катушки при резонансе равно реактивному сопротивлению конденсатора

X_Lo = 27if₀L = 2 • 3,14'Н ■ 21,8 • 102 • 10^_3= 14 0м

Напряжение на конденсаторе равно индуктивной составляющей

рис. ІО

Задачи 16-20 посвящены расчету разветвленных цепей переменного тока. Расчет разветвленных цепей переменного тока может быть выполненным одним из следующих методов:

1. графоаналитическим методом;

2. методом разложения токов на активные и реактивные составляющие;

3. методом проводимостей;

4. методом комплексных чисел (символическим методом).

Задачи 16-20 рекомендуется решать методом разложения токов на активные и реактивные составляющие.

Если параллельные ветви включают в себя емкостные и индуктивные сопротивления, то при равенстве реактивных проводимостей этих ветвей, то есть при b_L = b_c, в цепи наступает резонанс токов.

Пример 4

В сеть переменного тока напряжением U = 220 В и частотой f = 50 Гц включены параллельно: катушка с параметрами Ri= 6 Ом и Li= 25,5мГ (первая ветвь); активное сопротивление R₂ = 4 Ом и конденсатор емкостью С₂=Ю60 мкФ (вторая ветвь) - рис. 12

Определить методом разложения токов на активные и реактивные составляющие токи в ветвях Ij; 1₂ и ток I в неразветвленной части цепи. Найти также угол сдвига между током I в неразветвленной части цепи и напряжением U. Построить в масштабе векторную диаграмму токов, отложив горизонтально вектор напряжения.

Определить емкость С₀ конденсатор, который следует установить вместо второй ветви, чтобы в цепи возник резонанс токов.

Решение.

Расчет выполним для каждой ветви отдельно, а затем для всей цепи.

1) Для первой ветви

Индуктивное сопротивление

X_L₁=2πfL!=2х3.14 • 50 • 25,5 • 10 -³=8 Ом;

Полное сопротивление

Ток по закону Ома

I₁ = U/Z₁ =220/10=22 А;

Коэффициент мощности

Cosф=R1/z1=6/10 = 0.6

sіпф = X_L1 / z1 =8/10 =0,8

Активная и реактивная составляющие тока

2.)Для второй ветви

Емкостное сопротивление

Х_с2 = 1/(2πfC₂)= 10⁶/2 • 3,14 • 50 • 1060 = 3 Ом;

Полное сопротивление

Ток по закону Ома

I₂=U/z₂= 220/5 =44 А;

Коэффициент мощности

СоБф₂ = R₂/z₂ = 4/5 = 0,8;

sіпф₂= х_с2 /z₂= 3/5 = 0,6

Активная и реактивная составляющие тока I

3)Для всей цепи

Активная и реактивная составляющие тока I в неразветвленной части цепи

Знак минус при реактивной составляющей тока означает, что нагрузка цепи имеет емкостный характер.

Тогда

Угол сдвига между током I в неразветвленной части цепи и напряжением U легко определяется через cos ф

Cos ф = I _а / I = 48,4 / 49,2 = 0,98; ф =11°

Ток I опережает приложенное напряжение на угол ф= 11

Векторная диаграмма построена на рис. 13 в масштабе mi = 5 А / см

Длины векторов токов:

;

За исходный вектор принимаем вектор напряжения, откладываем его горизонтально. Активные составляющие тока I_aj и 1_а2 совпадают по фазе с напряжением и откладываются в масштабе вдоль вектора напряжения. Вектор тока I_Pi имеет индуктивный характер и поэтому отстает от вектора напряжения U на угол 90 ° (откладывается вниз). Вектор тока I_Р2 является емкостным, т.е. опережает вектор напряжения U на угол 90 ⁰ (откладывается вверх).

Ток I определяется геометрически сложением векторов токов I₁ и I₂ т.е. I = I₁ +I₂.

Отключив вторую ветвь (R₂C₂), присоединим вместо нее конденсатор емкостью Со.

Резонанс токов характеризуется равенством реактивных составляющих токов ветвей I_L и I_с. Другими словами, при I в цепи будет иметь место резонанс токов.

Зная I_CO = 17,6 А, определяем сопротивление конденсатора:

X_c₀=U/I_c0 =220/ 17,6= 12,5 Ом.

Тогда емкость конденсатора:

Задачи 21-25 посвящены расчету трехфазных цепей переменного тока. Для их решения необходимо знание основных соотношений между линейными и фазными напряжениями и токами, формул мощности трехфазного потребителя, принципов расчета трехфазных цепей и построения векторных диаграмм (Частоедов, 15.1-15.8). Рассмотрим примеры.

Пример 5

Три одинаковые катушки включены звездой в трехфазную сеть с линейным напряжением U _л = 380 В (рис. 14) Активное сопротивление каждой катушки R=15 Ом, индуктивное х _L = 20 О м. Определить фазное напряжение и_ф; фазный I_ф и линейный I_л токи; Полную S, активную Р и реактивную Q мощности cos ф трехфазного потребителя.

Построить в масштабе т_и = 75В/см векторную диаграмму напряжений и токов.

Решение

1. Поскольку задана равномерная однородная нагрузка фаз, то даже при отсутствии нулевого провода фазные напряжения равны

U_ф = U_A = U_b = U_с = U_л / =380 / =220 В

2. Полное сопротивление каждой фазы

3. Токи фаз (они же линейные)

Іф = I_Л = U_ф/ Z_Ф = 220 / 25 = 8,8 А.

4. Коэффициент мощности фазы (а т.к. нагрузка фаз равномерная и однородная, то и всего трехфазного потребителя)

Cosф = R / Z_Ф = 15 / 25 = 0,6, следовательно, ф = 53 ⁰;

Sin ф=0,8.

5. Мощности трехфазного потребителя:

Полная S = 3 U_ф • I_ф= 3 • 220 • 8,8 = 5808 ВА = 5,808 кВА,

активная Р =3U_фI_Ф • cos ф = S cos ф = 5,808 • 0,6 = 3,485 кВт;

реактивная Q = ЗU_Ф I_Ф • sinф = S sinф =5,808* 0,8 = 4,646 квар.

6. Строим векторную диаграмму (рис. 15)

Длины векторов фазных токов в масштабе mi = 4А/см будут равны ІіФ = 1_Ф/ mi = 8,8 /4 =2,2 см. Длины векторов фазных напряжений в масштабе m _u = 40 В/см будут равны I_иф = U_ф /m_u = 220/75 = 2,93см. Вначале откладываем векторы фазных напряжений. Вектор U_A откладывается вертикально вверх, вектор U_B отстает от вектора U_A на 120°, а вектор U_c в свою очередь отстает от вектора U_B на 120°. Соединив ко

⇐ Предыдущая 12

Воспользуйтесь поиском по сайту: