 |
Из рассказа А.П.Чехова “Репетитор”.
|
|
|
|
Гимназист 7 класса Егор Зиберов, согласно условию, заключенному с отцом Удодовым, должен подготовить его двенадцатилетнего сына Петю для поступления в гимназию.
Начинаются занятия по арифметике.
............................................................................................................................
Учитель берет задачник и диктует:
- “Купец купил 138 аршинов черного и синего сукна за 540 рублей. Спрашивается, сколько аршин купил он того и другого, если синее стоило 5 рублей за аршин, а черное 3 рубля? “ Повторите задачу.
Петя повторяет задачу и тотчас же, ни слова не говоря начинает делить 540 на 138.
- Для чего же это вы делите? Постойте! Впрочем, так... продолжайте. Остаток получается? Здесь не может быть остатка. Давайте-ка я разделю!
Зиберов делит, получает 3 с остатком и быстро стирает.
“ Странно...-думает он, ероша волосы и краснея. - Как же она решается? Гм!... Это задача на неопределенные уравнения, а вовсе не арифметическая...”
Учитель глядит в ответы и видит 75 и 63.
..............................................................................................................
-Это задача, собственно говоря алгебраическая,- говорит он. - Ее с иксом и игрэком решить можно. Впрочем, можно и так решить. Я вот разделил... понимаете? Теперь вот надо вычесть... понимаете? Или вот что... Решите мне эту задачу сами к завтраму... Подумайте...
Петя ехидно улыбается. Удодов тоже улыбается. Оба они понимают замешательство учителя. Ученик 7 класса еще пуще конфузится, встает и начинает ходить из угла в угол.
- И без алгебры решить можно, - говорит Удодов, протягивая руку к счетам и вздыхая. - Вот, извольте видеть...
Он щелкает на счетах, и у него получается 75 и 63, что и нужно было.
Попробуйте и Вы решить задачу А.П.Чехова.
|
|
|
Геометрический материал.
Поверхность прямоугольного параллелепипеда и куба.

1. Начертить несколько различных разверток куба, ребро которого 5 см.
2. Ребро куба 10 см. Вычислить площадь полной его поверхности.
3. Вычислить площадь полной поверхности куба, ребро которого 1м; 1дм; 15см; 50см; 3 дм; 5 дм; 4 дм;
4. Начертить развертки параллелепипедов, имеющих следующие размеры:
а) длину 3 см; ширину 2 см; высоту 2 см;
б) длину 3 см; ширину 2 см; высоту 4 см;
5. Вычислить площадь полной поверхности параллелепипедов, размеры которых:
| длина | ширина | высота |
| 8см 5см 3дм 2дм | 5см 2см 2дм 1дм | 5см 2см 2дм 6дм |
6. Длина комнаты 8 м, ширина 5 м и высота 4 м. Вычислить:
а) площадь пола;
б) площадь потолка;
в) площадь всех стен;
7. Комнату длиной 8 м, шириной 6 м и высотой 4 м нужно оштукатурить. Сколько будет стоить штукатурка стен и потолка, если за 1 м2 мастер берет 1 лат 80 сантимов.
Указание: площадь окон и дверей не исключать.
8. Комнату длиной 6 м, шириной 4 м и высотой 3 м нужно оклеить обоями. Сколько потребуется обоев, если длина рулона 6м, ширина 5 дм, а площадь окон и дверей составляет 12 м2?
9. Зал длиной 15 м, шириной 12 м и высотой 5 м имеет 8 окон и 2 двери. Ширина и высота окна 1м 5 дм и 2м 5 дм. Ширина и высота двери 2 м и 3 м 5 дм. Сколько будет стоить побелка стен и потолка этого зала, если за побелку 1 м2 платить по 40 сантимов и если площадь окон и дверей исключить?
10. Кусок меди имеет форму прямоугольного параллелепипеда, длина которого 7 дм, ширина 2 дм 5 см. Шлифовка 1 дм2 поверхности стоит 15 сантимов. Какой толщины этот кусок, если шлифовка всей поверхности стоила 13 латов 80 сантимов?
11. Гранитная плита имеет форму прямоугольного параллелепипеда. Шлифовка ее поверхности стоила 123 лата 12 сантимов, по 18 сантимов за квадратный дециметр. Какова толщина этой плиты, если длина ее 1 м 5 дм, а площадь основания 1м280дм2?
|
|
|
Треугольник.

Черт. 1
12. Назвать треугольники, изображенные на чертеже 1, обращая внимание на углы этих треугольников.

Черт. 2
13. Назвать треугольники, изображенные на чертеже 2, обращая внимание на стороны этих треугольников.
14. Измерить стороны треугольников, изображенных на чертеже 2. Вычислить сумму длин сторон (периметр) каждого из них.
15. Периметр равнобедренного треугольника 145 м. Каждая из двух равных его сторон на 2 м больше третьей. Вычислить стороны треугольника.
16. Периметр равнобедренного треугольника 13 см. Сумма равных его сторон на 7 см больше третьей стороны. Вычислить длину каждой стороны треугольника.
17. Начертить квадрат, стороны которого равны каждая 4 см, и разделить его на два равных треугольника. Вычислить площадь каждого треугольника.
18. Начертить прямоугольник, стороны которого равны 4 см и 3 см; разделить его на два равных треугольника. Вычислить площадь каждого треугольника.
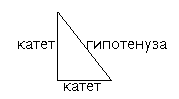
Черт.3
19. Вычислить площади прямоугольных треугольников, катеты (см. черт.3) которых: 15 см и 8 см; 7 см и 5 см; 24 см и 13 см; 50м и 27 м; 1м 4дм и 7 дм;
20. Участок земли, имеющий форму прямоугольного треугольника, окопали канавой. Длина одного его катета 45 м, другой катет на 35 м длиннее; гипотенуза (см. черт.3) на 11 м длиннее второго катета. Вычислить площадь участка и длину канавы.
Окружность.

Черт.4
21. Начертить три окружности: радиус (см. рис. 4) одной из них 2 см, радиус другой 3 см, радиус третьей 5 см.
22. Начертить две окружности, имеющие один и тот же центр; радиус одной из них 3 см; радиус другой 2 см 5 мм.
23. Начертить две пересекающиеся окружности по следующим данным: радиус одной окружности 3 см, радиус другой 4 см, расстояние между их центрами 5 см.
24. Начертить две окружности: диаметр одной из них 6 см, диаметр другой на 2 см длиннее.
25. Радиус окружности 3 см. Чему равен ее диаметр?
26. Диаметр окружности 8 дм. Чему равен ее радиус?
27. Диаметр колеса 7 дм, а длина окружности содержит немного больше 3 диаметров. Какой длины шина этого колеса?
|
|
|
28. Радиус земного экватора 6400 км; экватор приблизительно в 3 раза длиннее своего диаметра. Вычислить длину экватора.
29. Колесо, имеющее в окружности 35 дм, обернулось на некотором расстоянии 50 раз. Сколько раз на том же расстоянии обернется другое колесо, имеющее в окружности 25 дм?
30. Переднее колесо автомобиля делает 39 оборотов в то время, когда заднее делает только 23 оборота. Сколько оборотов сделает заднее колесо, когда переднее обернется 936 раз?
31. Заднее колесо экипажа, имеющее в окружности 2 м 5 см, на некотором расстоянии обернулось 10080 раз. Сколько раз в то же время и на том же расстоянии обернулось переднее колесо, окружность которого на 85 см меньше окружности заднего колеса?
|
|
|


