 |
Решение методом контурных токов
|
|
|
|
Для рассматриваемой цепи (см. рис. 2.2) система уравнений относительно контурных токов 
, совпадающих по направлению с обходом контуров, имеет вид
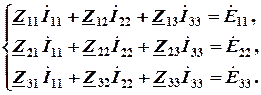(2.1)
В данной системе:
– собственные сопротивления контуров:
;
;
;
– общие сопротивления контуров:
;
;
;
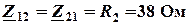– контурные ЭДС:
В выбранной совокупности контуров
.
Следовательно, первое уравнение в системе (2.1) может быть исключено из совместного рассмотрения при ее решении относительно неизвестных контурных токов 
и 
. После подстановки численных значений система (2.1), сокращенная на одно уравнение, примет вид
Решать данную систему целесообразно с применением правила Крамера.
Определители системы:
Токи и находят по формулам:
,
.
В соответствии с условно принятыми положительными направлениями (см. рис. 2.2) вычислим токи ветвей:
Мгновенные значения токов ветвей и напряжения на источнике тока
Поскольку угловая частота равна w = 2p f, а амплитуда связана с действующим значением с помощью соотношения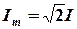 
, следовательно,
где 
- начальная радиан-фаза тока i 1,
аналогично запишем:
Баланс активных и реактивных мощностей
Комплексная мощность источников:
,
где 
и 
– сопряженные комплексы тока.
Комплексная мощность потребителей:
,
где активная мощность:
,
реактивная мощность:
(в формулах мощности потребителей I i – действующие значения токов).
Относительная погрешность расчета:
.
Построение топографической диаграммы
 |
На рис. 2.3 представлена векторная диаграмма токов ветвей рассматриваемой схемы в соответствии с масштабом по току МI: 1 деление – 0,5 А. Диаграмма токов позволяет проверить графическим путем выполнение соотношений по I закону Кирхгофа.
|
|
|
В соответствии с принятыми на рис. 2.2 обозначениями рассчитываются значения потенциалов точек цепи. Потенциал точки А принимается равным нулю.
проверка 1: 
проверка 2: 
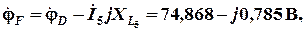
проверка 3: 
Выбираем масштаб по напряжению МU для построения диаграммы: 1 деление – 20 В.
 |
На рис. 2.4 изображена топографическая диаграмма напряжений, позволяющая проверить графическим путем выполнение соотношений по II закону Кирхгофа.
На рис. 2.5 изображена совмещенная диаграмма токов и напряжений, позволяющая проверить выполнение соотношений по закону Ома в символической форме для всех пассивных элементов цепи.
 |
2.4.6. Метод узловых потенциалов
Для рассматриваемой цепи (рис. 2.6), содержащей 4 узла, система, составленная в соответствии с методом узловых потенциалов, должна содержать 3 уравнения. Выберем в качестве опорного узел 4.
Имеем:
Так как в цепи имеется ветвь с идеальным источником ЭДС, потенциал узла 1 известен и равен 
. Таким образом, число неизвестных потенциалов сокращается до двух, и, соответственно, число совместно рассматриваемых уравнений в системе сократится до двух:
 |
собственные узловые проводимости:
общие узловые проводимости:
; 
; 
узловые токи: 
.
Решив систему уравнений, определим неизвестны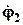е 
и 
. Далее, используя обобщенный закон Ома, рассчитаем токи ветвей:
Ток 
определим по I закону Кирхгофа:
.
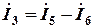Напряжение на источнике тока определим по II закону Кирхгофа:
.
Проверка баланса мощностей и расчет потенциалов точек для построения векторной диаграммы ведется в соответствии с алгоритмом, приведенным в пп. 4.2.4, 4.2.5.
Метод наложения
С использованием принципа суперпозиции рассчитывается ток 
. Поскольку в цепи два источника, для определения искомого тока строятся две подсхемы, каждая из которых содержит только один из источников, а второй исключается в соответствии с правилом, изложенным в п.п. 3.4.
|
|
|
Расчет составляющей 
по схеме (рис. 2.7)
.
.
Расчет составляющей 
по схеме (рис. 2.8)
.
Искомый ток
.
|
|
|
