Главная | Обратная связь | Поможем написать вашу работу!

Пример использования алгоритма для решения задачи .

⇐ ПредыдущаяСтр 2 из 2

Задача С2. Тема: "Равновесие составной конструкции, находящейся под действием произвольной плоской системы сил"

Конструкция состоит из жесткого угольника и стержня, которые в точке С свободно опираются друг о друга.

На конструкцию наложены внешние связи:

- в точке А жесткая заделка;

- в точке В шарнир;

На конструкцию действуют:

- пара сил с моментом М = 50 кН·м;

- равномерно распределенная нагрузка интенсивности q = 10 кН /м;

- две силы, F₁=10 кН, и F₂=20 кН, приложенные в точках K и L соответственно.

Определить реакции связей в точках А, В, С. При окончательных расчетах принять а=0,5м

B o

60⁰ - K F₂

F₁

30⁰L 45⁰

Рис.1

Решение задачи.

Применим для решения задачи приведённый выше алгоритм.

Выбираем объект равновесия.

Рассмотрим отдельно равновесие стержня ВС (I) и жёсткого угольника ACL (II), т.е. будем решать две задачи на равновесие. ¹

Первая часть. Задача I.

1. Итак, объект равновесия выбран – это стержень ВС (жёсткий угольник ACL в этой части задачи рассматриваем как связь наложенную на ВС).

2. Составим расчётную схему задачи: к свободному стержню ВС приложим все заданные силы –пару сил

3. с моментом М, силу F₁, и реакции связей – X_B_,Y_B, Y_C. Расчётная схема готова (Рис.2).

Y_B

X_B

M K

60⁰ Y_C

F₁

30⁰C

O X

Рис.2

4. Для полученной на расчётной схеме уравновешенной произвольной плоской системы сил составим три независимых уравнения равновесия в форме:

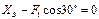(1)

(2)

(3)

5. Можно сразу решить систему алгебраических уравнений (1)-(3) относительно неизвестных X_B, Y_B, Y_C, т.к. число неизвестных и число уравнений совпадает (если бы число неизвестных превышало число уравнений, то нужно было бы составить уравнения равновесия для второй части составной конструкции, а затем решать систему шести уравнений равновесия, полученных на двух этапах, относительно шести неизвестных).

Из (1)

Из (3)

Из (2)

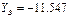Н, знак минус перед модулем вертикальной составляющей реакции подшипника В указывает на то, что она направлена по вертикали вниз, а не вверх, как мы предположили.

Итак мы нашли неизвестные, входящие в первую часть задачи:

6. Последние два пункта алгоритма выполним после решения второй части задачи (это особенность решения задач на равновесие составных конструкций).

Вторая часть. Задача 2.

1. Рассмотрим равновесие жёсткого угольника АСL.

2. Составим расчётную схему (рис.3):

к угольнику приложим заданные силы F ₂и Q, которой мы заменили равномерно распределённую на участке CL нагрузку интенсивности q:

(Н);

и реакции связей – Х_А, Y_A, M_A (момент пары сил, возникающей в жёсткой заделке), а также реакция Y’_C- сила действия стержня ВС на угольник ACL (по модулю Y’_С= Y_c=16.347 H).

3. Для полученной на расчётной схеме уравновешенной произвольной плоской системы сил составим три независимых уравнения равновесия в форме:

(4)