 |
Применение ММИ для доказательства неравенств
|
|
|
|
МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Доронина Диана Александровна,
Учащаяся 10 «А» класса
Богданова Дарья Олеговна,
Учащаяся 10 «А» класса
Руководитель
Скоринкина Мария Мечиславовна,
Учитель математики
Витебск 2016
СОДЕРЖАНИЕ
Введение 4
Глава 1. Применение ММИ в задачах на суммирование 4
Глава 2. Применение ММИ для доказательства неравенств 5
Глава 3. Применение ММИ в задачах на делимость 4
Глава 4. Применение ММИ в геометрических задачах 6
Глава 5. Применение ММИ для изучения свойств
числовых последовательностей 7
Глава 6. Применение ММИ для изучения свойств конечных
множеств 8
Глава 7. Подборка задач для самостоятельного решения 9
Заключение 14
Список использованных источников 15
ВВЕДЕНИЕ
При подготовке к районной олимпиаде по математике нам встретилась задача, для решения которой понадобились знания по теме ММИ. Однако школьное пособие не содержит нужной нам информации, и тогда мы решили при помощи дополнительной литературы более подробно изучить данный метод.
Метод математической индукции (ММИ) относится к самым важным методам математических доказательств. Он применяется для доказательства утверждений, зависящих от натурального числа. Существует несколько разновидностей метода математической индукции. Мы познакомимся с самой простой из них.
Предположим, в одну бесконечную цепочку выстроены кости домино. Если они установлены достаточно близко друг от друга – так, что любая из них, падая, опрокинет следующую стоящую за ней костяшку, мы повалим все. В этом и состоит суть ММИ, который мы ниже сформулируем более строго.
Предположим, что требуется проверить справедливость некоторого высказывания относительно произвольного натурального числа n. Тогда:
|
|
|
1. Если это высказывание истинно для некоторого начального значения  , например, для
, например, для  (например, опрокидывается первая кость домино);
(например, опрокидывается первая кость домино);
2. Из справедливости этого высказывания для значения  следует справедливость его для следующего значения
следует справедливость его для следующего значения  (например, очередная k-я кость опрокидывает следующую
(например, очередная k-я кость опрокидывает следующую  -ю), то это высказывание справедливо для любого натурального
-ю), то это высказывание справедливо для любого натурального  .
.
Данная тема является сегодня актуальной, выросла ее область применения, однако, материала для изучения и применения ММИ в школьных учебниках недостаточно.
Гипотеза: ММИ поможет при решении ряда задач
Цель исследования: изучение метода математической индукции.
Для достижения поставленной цели были поставлены следующие задачи:
1. Систематизировать знания по теме ММИ
2. Применить ММИ при решении математических задач и доказательств теорем
3. Обосновать и наглядно показать практическое значение ММИ
Применение ММИ в задачах на суммирование
Пример 1. Докажите методом математической индукции истинность равенства 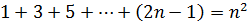 .
.
Решение.
1) При  левая часть содержит одно слагаемое 1, а правая часть равна
левая часть содержит одно слагаемое 1, а правая часть равна  . Поэтому доказываемое равенство принимает вид:
. Поэтому доказываемое равенство принимает вид: 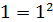 . Это верное равенство, значит, при
. Это верное равенство, значит, при  равенство
равенство 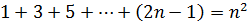 истинно.
истинно.
2) Предположим равенство 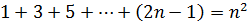 истинно при
истинно при  , т.е. что справедливо равенство
, т.е. что справедливо равенство  . Докажем, что тогда равенство
. Докажем, что тогда равенство 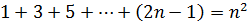 истинно и при
истинно и при  , т.е. что справедливо равенство
, т.е. что справедливо равенство  . Имеем:
. Имеем:  . Но по предположению индукции сумма в квадратных скобках равна
. Но по предположению индукции сумма в квадратных скобках равна  . Значит, вся сумма равна
. Значит, вся сумма равна  . Итак,
. Итак, 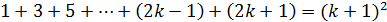 . Тем самым по принципу математической индукции истинность равенства
. Тем самым по принципу математической индукции истинность равенства 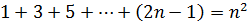 доказана для любых
доказана для любых  .
.
Пример 2. Докажите: 
Решение.
Пусть  . Воспользуемся методом математической индукции:
. Воспользуемся методом математической индукции:
1)  истинно, так как
истинно, так как  .
.
2) Пусть  . Допустим, что
. Допустим, что  истинно, т.е. верно равенство
истинно, т.е. верно равенство  . Прибавим к обеим частям этого равенства
. Прибавим к обеим частям этого равенства  . Получим:
. Получим:  , а это означает, что
, а это означает, что  истинно. Следовательно, равенство верно при любом натуральном
истинно. Следовательно, равенство верно при любом натуральном  .
.
|
|
|
Применение ММИ для доказательства неравенств
Пример 1. Докажите неравенство: 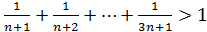 ,
, 
Решение.
Докажем данное неравенство методом математической индукции.
1) Если  , то
, то  .
.
2) Предположим, что данное неравенство верно при  ,
, 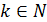 , т.е.
, т.е.  .
.
3) Докажем, что неравенство верно и при  , т.е.
, т.е.  .
.
Следовательно, необходимо доказать, что  .
.
Действительно,  для
для 
Таким образом, неравенство верно при  , следовательно, оно будет верным при любом натуральном
, следовательно, оно будет верным при любом натуральном  .
.
Пример 2. Докажем неравенство:  .
.
Решение.
1) Выражение, содержащееся в левой части неравенства  , представляет собой сумму дробей, знаменатели которых последовательно растут от 1 до
, представляет собой сумму дробей, знаменатели которых последовательно растут от 1 до  . При
. При  оно обращается в 1. Но
оно обращается в 1. Но 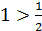 - истинное неравенство, следовательно, неравенство
- истинное неравенство, следовательно, неравенство  верно при
верно при  .
.
2) Предположим, что  .
.
3) Докажем, что тогда 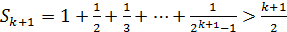 .
.
4) В самом деле, имеем:  .
.
Итак, 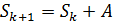 , где
, где  . Выражение
. Выражение  представляет собой сумму
представляет собой сумму  дробей, каждая из которых больше, чем
дробей, каждая из которых больше, чем  . Значит,
. Значит,  . Поскольку
. Поскольку  ,
, 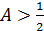 , то отсюда следует, что
, то отсюда следует, что 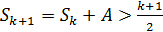 .
.
Истинность неравенства  доказана.
доказана.
|
|
|


