 |
Часть II. «Вариационные принципы. Стохастические модели.»
|
|
|
|
(Л.Т. Моисеева, МЕТОДЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ПРОЦЕССОВ В МАШИНОСТРОЕНИИ. См. МетМатМодМоисеева.doc)
Вариационные принципы.
Задание 2.1. Пусть заданы координаты точек А и С. Точка В лежит на прямой y =0. Используя вариационные принципы построения математических моделей, найти:
а) условие, при котором ломаная АВС имеет наименьшую длину;
б) числовое значение этого условия;
в) наименьшую длину ломаной АВС.
| 3.1. А (-5;10), С (25;15); 3.2. А (5;15), С (30;5); 3.3. А (0;5), С (25;10); 3.4. А (-10;15), С (20;10); 3.5. А (5;10), С (30;15); | 3.6. А (-5;5), С (15;15); 3.7. А (-10;5), С (20;15); 3.8. А (0;10), С (25;5); 3.9. А (5;5), С (30;10); 3.10. А (-5;15), С (25;10). |
Стохастические модели
В практике современных исследований сложных систем, явлений, объектов широкое распространение получили методы математического моделирования и на их основе – вычислительные эксперименты.
Важнейшим классом математических моделей являются так называемые эмпирические модели.
Исходными данными для разработки эмпирических моделей являются экспериментальные данные, полученные в результате проведения экспериментальные данные, полученные в результате проведения экспериментов с целью выявления значений параметров исследуемых явлений, процессов или объектов.
Эмпирические модели являются наиболее эффективным средством представления результатов экспериментов в системах математического моделирования.
Предполагается, что имеющиеся экспериментальные данные дают достаточно информации для построения математической модели изучаемого явления, процесса или объекта.
На основании экспериментальных результатов требуется построить математическую модель системы, то есть описать изучаемую систему (явление, процесс, объект) некоторыми математическими соотношениями, создать математическую модель системы. В большинстве случаев экспериментальные данные представляют собой случайные величины.
|
|
|
Во многих задачах требуется установить и оценить зависимость случайной величины Y от одной или нескольких других случайных величины X.
Пусть изучается система двух количественных случайных признаков (X, Y) некоторого процесса, явления или объекта, когда обе величины X и Y или одна из них подвержены действию случайных факторов. В этом случае между величинами X и Y имеет место стохастическая зависимость. Требуется установить аналитическое выражение этой зависимости, то есть составить математическую модель процесса.
Чтобы получить заданную зависимость, необходимо иметь выборку её наблюдений. Такой выборкой являются результаты n независимых экспериментов, представленные n парами случайных значений (x1, y1), (x2, y2),… (x1, y1) экспериментальных (статистических) данных.
Математическая модель, построенная на основе имеющейся выборки (xi, yi), i=1,…,n экспериментальных (статистических) данных имеет вид:
Y=f(x)
И представляет собой так называемое уравнение парной регрессии. В этом уравнении Y называют зависимой переменной (или результативным признаком); x –независимой, или объясняющей переменной (признак-фактор).
Уравнение парной регрессии широко используется во многих прикладных задачах, в частности, при построение математических моделей разнообразных по своему характеру задачах экономики.
Любое экономическое исследование начинается со спецификации модели, то есть с формулировки вида модели, исходя из соответствующей теории связи между переменными. Прежде всего из всего круга факторов, влияющих на результативный признак (Y) выделяют наиболее существенно влияющие факторы. Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной (x). Уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как некоторая закономерность лишь в среднем по совокупности наблюдений. Практически в каждом отдельном случае фактическая величина результативного признака (yi) складывается из теоретического значения результативного признака yi(xi,), найденного из уравнения регрессии, и случайной величины εi, характеризующей отклонение фактического значения результативно признака Yi от его расчетного значения yi(xi,). Случайная величина (возмущение) εi включает влияние неучтенных в модели факторов. Её наличие вызвано тремя источниками: спецификацией модели, выборочным характером эмпирических данных, особенно измерения переменных величин. Величина случайных ошибок εi зависит от правильного осуществления этапа спецификации модели. Предполагая, что ошибки измерения переменных сведены к минимуму, основное внимание уделяется ошибкам спецификации модели.
|
|
|
Выбор математической функции y=f(x) в случае парной регрессии может быть осуществлен тремя способами: графическим, аналитическим (то есть из теории изучаемой взаимосвязи) и экспериментальным.
Аналитический метод выбора типа уравнения регрессии основан на изучении материальной природы связи изучаемых признаков.
При компьютерной обработки исходной информации, предназначенной для выбора вида уравнения регрессии, такой выбор обычно осуществляется экспериментальным методом, то есть путем сравнения величины остаточной дисперсии
рассчитываемой для разных моделей.
Чем меньше величина остаточной дисперсии, тем в меньшей мере имеет место влияние не учитываемых в уравнение регрессии факторов, тем лучше уравнение регрессии подходит к исходным данным. При обработке на компьютере исходных статистических данных в автоматическом режиме перебираются разные математические функции и из них выбирается та, для которой остаточная дисперсия является наименьшей.
Если остаточная дисперсия оказывается примерно одинаковой для нескольких функций, то предпочтение отдается более простым видам функций, поскольку они в большей степени поддается интерпретации и требуют меньшего объема наблюдений. Если вид функции усложняется, то требуется увеличение объема наблюдений, поскольку, как показывают результаты многих исследований, число наблюдений должно в 6-7 раз превышать число рассчитываемых параметров при переменной x. Так каждый параметр при x должен рассчитываться хотя бы по 7 наблюдениям. Если, например, в качестве математической модели исследуемого явления, процесса, объекта выбирается парабола второй степени 
, то требуемой исходный объем информации должен содержать не менее 14 наблюдений. При выборе спецификации модели предпочтительнее модель с меньшим числом параметром при x.
|
|
|
При изучении зависимости между двумя переменными достаточно удобен и поэтому широко применяется геометрический метод подбора вида уравнения регрессии, который заключается в следующем.
Пусть имеются два ряда эмпиричеcких данных x(x1,x2,…,xn) и y(y1,y2,…,yn).Соответствующие им точки с координатами (xi,yi), i=1,…,n, изображаются координатной плоскости. Такое изображение исходной статической зависимости называется полем корреляции. По расположению эмпирических точек поля корреляции делается предположение (высказывается гипотеза) о наличии предельного вида регрессивной зависимости. Между переменными x и y, то есть о математической модели изучаемого явления, процесса, объекта.
При количественной оценки связей между двумя переменными x и y на практике широко используются математические функции вида:
,
и ряд других функций.
Эффективным методом отыскания значений неизвестных коэффициентов (параметров) таких функций является метод наименьших квадратов (МНК).
Согласно методу наименьших квадратов неизвестные параметры принятой математической модели выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значений yi от значений yi (xi), найденных по уравнению регрессии была минимальной: 
Оценим параметры a0, a1 в случае линейной парной регрессии , используя для этого метод наименьших квадратов.
Следует отметить, что для оценки параметров a0 и a1 возможны и другие подходы. Так, например, согласно методу наименьших модулей следует минимизировать суму абсолютных значений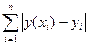 
.
|
|
|
Однако метод наименьших квадратов существенно проще при проведении вычислительной процедуры и дает хорошие по статистическим свойствам оценки. Этим и объяснятся его широкое применение в статистическом анализе.
Согласно методу наименьших квадратов составим сумму квадратов отклонений эмпирических значений yi от значений yi(xi), найденных по уравнению парной регрессии:
В силу необходимого условия существования экстремума (минимума) функции двух переменных S(a0,a1) приравняем к нулю её частные производные по a0 и a1. Получим:
После преобразований получим систему двух линейных уравнений относительно значений искомых параметров a0 и a1 следующего вида:
Полученная система называется системой нормальных уравнений. Решая эту систему, найдем искомые оценки параметров a0 и a1 уравнения линейной парной регрессии.
Рассмотрим в качестве примера зависимость вежду величиной основных производственных фондов X и следующей выработкой продукции Y. По данным пяти независимых наблюдений, представленным в таблице:
| i | |||||
| xi | 1.00 | 1.50 | 3,00 | 4.50 | 5.00 |
| yi | 1.25 | 1.40 | 1.50 | 1.75 | 2.25 |
Изобразив указанную статистическую зависимость графически точками координатной плоскости (то есть построив поле корреляции), по расположению эмпирических точек можно предполагать наличие линейной регрессионной зависимости между переменными X и Y. Поэтому уравнение регрессии будем искать в виде линейного уравнения .
По данным независимых наблюдений, представленным в таблице, вычислим все суммы, необходимые для составления системы нормальных уравнений относительно искомых значений параметров a0 и a1 линейного уравнения регрессии. Получим:
=1+1,5+3+4,5+5=15;
=1+2,25+9+20,25+25=57,50;
=1,25+1,4+1,5+1,75+2,25=8,15;
Теперь составим систему нормальных уравнений:
Полученную систему можно решить любым из известных методов. Например, в соответствии с методом Крамера вычислим:
Теперь находим:
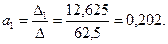
Следовательно, искомое уравнение линейной парной регрессии (то есть математическая модель процесса) имеет вид: 
Из полученного уравнения следует, что при увеличим основных производственных фондов X на одну денежную единицу, суточная выработка предприятия увеличится в среднем на 0,202 (условных единиц).
Правильность спецификации модели проверяется с помощью коэффициента корреляции
, где
,
- выборочные дисперсии переменных x и y соответственно.
Вычислим их значения
; 
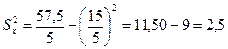следовательно, 
.
Очевидно, что связь между рассматриваемыми переменными X и Y достаточно тесная: величина коэффициента корреляции составила 0.9, что достаточно близко к 1 и означает наличие тесной связи между величиной основных производственных фондов X и суточной выработкой продукции Y.
|
|
|
Оценим значимость уравнения регрессии.
В случае линейной парной регрессии уравнение значимо (адекватно имеющимся статистическим данным), если для значения критерия F Фишера-Снедокора выполняется неравенство
, где m – количество параметров модели.
Вычислим значение
Зададимся, например, уровнем замости, равным α=0.05 (вероятность совершить так называемую ошибку первого рода, то есть отвернуть правильную гипотезу о виде математической модели) при числе степеней свободы k=n-m-1, где m=2 количество независимых коэффициентов (параметров) математической модели. По таблице F-распределения находим 
(критическое значение F): 
.
Так как фактическое (наблюдаемое) значение 
меньше 
:
=12.79 < = =18.5, то гипотеза о адекватности (значимости) модели реальному процессу принимается.
В случае квадратичной зависимости 
В соответствии с методом наименьших квадратов имеем:
Вычисляем и приравниваем нулю частные производные:
После преобразований получаем нормальную систему следующего вида:
Для составления этой системы согласно исходным статистическим данным предварительно вычисляются все сумы, являющиеся коэффициентами и свободными членами нормальной системы.
Пример: Найдем оценки параметров математической модели по заданным статистическим данным:
| i | |||||
| xi | |||||
| yi |
Решение:
=1+2+3+4+5=15,
=1+4+9+16+25=55
=1+8+27+64+125=225
=1+16+81+256+625=979
=6+9+10+12+13=50
=1·6+2·9+3·10+4·12+5·13=6+18+30+48+65=167
=1·6+4·9+9·10+16·12+25·13=6+36+90+192+325=649
Теперь составим нормальную систему:
Вычислим: 
=700; 
; 
; 
Находим: 
Следовательно: 
В случае кубической зависимости 
Имеем:
После преобразований получаем нормальную систему следующего вида:
Для составления этой системы вычисляются все указанные в ней суммы.
Литература
1. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для втузов.-М.: Высшая школа, 1977-479 с.
2. Крмер Н.Ш.Теория вероятностей и математическая статистика: Учебник для вузов. –М.: ЮНИТИ –ДАНА, 2000.-543с.
Задание 2.2. Провести идентификацию эмпирической математической модели.
А) Предполагается, что процесс описывается одномерным уравнением 2-го порядка
W = a 0 + a 1 x + a 2 x 2, 0 £ x £ 10.
Б) Предполагается, что процесс описывается одномерным уравнением 3-го порядка
W = a 0 + a 1 x + a 2 x 2+ a 3 x 3 0 £ x £ 10.
Считаем, что величина х измеряется точно, а W – с ошибкой e, имеющей нормальное распределение с нулевым математическим ожиданием и единичной дисперсией М (e) = 0, s2(e) = 1. Проверить адекватность модели методом Фишера и сравнить модели А) и Б) графически с моделью линейной регрессии.
| № Вар.\ № точки | ||||||||||||
| ||||||||||||
| W | 22,52 | 34,5 | 27,2 | 38,5 | 50,8 | 61,8 | 60,7 | 71,9 | 72,2 | 83,9 | ||
| 29,7 | 33,4 | 44,5 | 53,3 | 60,4 | 73,8 | 87,8 | ||||||
| 28,9 | 31,5 | 50,3 | 42,1 | 63,4 | 58,8 | 79,3 | 74,1 | 93,6 | 92,6 | 108,6 | ||
| 28,3 | 22,6 | 38,2 | 50,9 | 72,4 | 74,9 | 86,3 | 79,9 | 101,8 | ||||
| 20,81 | 33,95 | 40,39 | 50,6 | 59,3 | 59,7 | 56,1 | 86,8 | 73,9 | 94,6 | |||
| 11,4 | 25,6 | 31,5 | 38,4 | 50,7 | 52,4 | 66,3 | 74,6 | 78,2 | 95,5 | |||
| 21,1 | 20,7 | 32,7 | 40,8 | 54,6 | 53,4 | 66,5 | 77,7 | 81,6 | 88,8 | 98,3 | ||
| 15,7 | 14,8 | 21,4 | 22,3 | 30,6 | 32,7 | 38,4 | 36,5 | 39,9 | 49,4 | 49,1 | ||
| 18,1 | 25,3 | 29,4 | 28,5 | 36,5 | 47,6 | 45,2 | 65,3 | |||||
| 12,9 | 32,25 | 42,8 | 69,6 | 68,2 | 89,7 | 105,6 |
Контрольные вопросы.
1. Что является исходным материалом при построение эмпирической модели?
2. Каковы цели и задачи спецификации эмпирической модели?
3. В чем заключается организация процесса математического моделирования?
4. В чем стоит подготовка информационной базы математического моделирования?
5. В чем заключаются статистические методы обработки экспериментальных данных?
6. Что представляет собой спецификация моделей парной регрессии?
7. Каков критерий качества спецификации математической модели?
8. Каковы методы выбора математической модели?
9. В чем состоит метод наименьших квадратов?
10. Что такое уравнение регрессии?
|
|
|
