 |
Исследование функций характеристических сопротивлений
|
|
|
|
Характеристические сопротивления 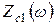 ,
, 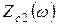 определяются с помощью выражений
определяются с помощью выражений
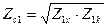 ,
,  , (4.1)
, (4.1)
где 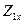 ,
,  - общие сопротивления холостого хода (XX) четырёхполюсника рисунка 2.2 (соответствующего вашему фильтру) относительно зажимов 1-1' и 2-2’ соответственно;
- общие сопротивления холостого хода (XX) четырёхполюсника рисунка 2.2 (соответствующего вашему фильтру) относительно зажимов 1-1' и 2-2’ соответственно;
 - сопротивления короткого замыкания (КЗ) – общее сопротивления относительно зажимов 1-1’ при коротком замыкании зажимов 2-2’;
- сопротивления короткого замыкания (КЗ) – общее сопротивления относительно зажимов 1-1’ при коротком замыкании зажимов 2-2’;
 - сопротивления КЗ – общее сопротивления относительно зажимов 2-2’ при коротком замыкании зажимов 1-1’.
- сопротивления КЗ – общее сопротивления относительно зажимов 2-2’ при коротком замыкании зажимов 1-1’.
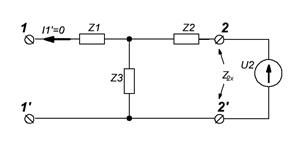
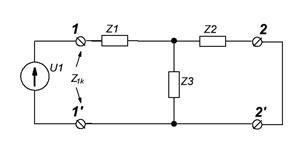
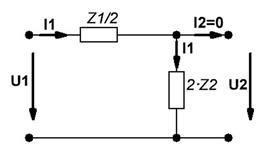
Пример 4.1. Для несимметричного Т-образного четырёхполюсника рисунка 4.1:
- так как в режиме ХХ относительно зажимов 2-2’ - I2=0 (рисунок 4.1,а), то
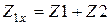 ;
;
- в режиме ХХ относительно зажимов 1-1’ - I1’=0 (рисунок 4.1,б), то
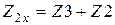 ;
;
- в режиме КЗ относительно зажимов 2-2’ (рисунок 4.1,в)
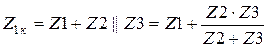 ;
;
- в режиме КЗ относительно зажимов 1-1’ (рисунок 4.1,г)
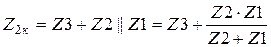 .
.
 а)
а)
|  б)
б)
|
 в)
в)
|  г)
г)
|
Рисунок 4.1 – Схемы одного и того же четырёхполюсника для определения сопротивлений холостого хода и короткого замыкания
Учитывайте, что для симметричных четырёхполюсников справедливо
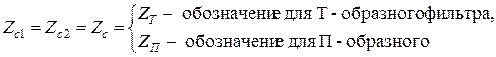 . (4.2)
. (4.2)
Зависимости  и
и  рекомендуется определять в следующей последовательности:
рекомендуется определять в следующей последовательности:
a) Получить выражения для сопротивлений 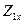 ,
,  ,
,  ,
,  в общем виде относительно переменных Z1 и Z2 (подобным образом получены соответствующие выражения в примере 4.1).
в общем виде относительно переменных Z1 и Z2 (подобным образом получены соответствующие выражения в примере 4.1).
b) Подставить полученные выражения в (4.1).
c) Затем, подставив вместо Z1 и Z2 их частотные выражения Z1(w) и Z2(w), полученные в пункте 2.2, получить частотные зависимости 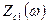 ,
, 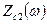 .
.
Построив диаграммы 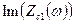 ,
, 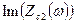 ,
, 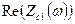 и
и 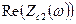 , проверить выполнение соответствующих условий в таблицах 2.3 или 2.4 в полосах пропускания и задерживания.
, проверить выполнение соответствующих условий в таблицах 2.3 или 2.4 в полосах пропускания и задерживания.
Анализ A-параметров
A-параметры являются коэффициентами системы
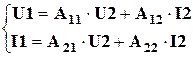 , (4.3)
, (4.3)
определяемые в режимах ХХ и КЗ:
|
|
|
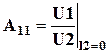 ,
, 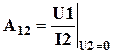 ,
, 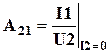 ,
, 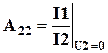 . (4.4)
. (4.4)
Полученные частотные зависимости 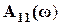 ,
, 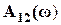 ,
, 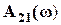 ,
, 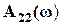 используются для проверки признаков ПП и ПЗ в 4-й строке таблицы 2.4 (для симметричных фильтров), а также во 2-х и 3-х строках таблиц 2.3 и 2.4.
используются для проверки признаков ПП и ПЗ в 4-й строке таблицы 2.4 (для симметричных фильтров), а также во 2-х и 3-х строках таблиц 2.3 и 2.4.
Пример 4.2. Определим A-параметры для фильтра рисунка 4.2 - Г-четырёхполюсника с Т-входом.

Рисунок 4.2 – Избирательный Г-четырехполюсник с Т-входом
В рассматриваемом фильтре
 , (4.5)
, (4.5)
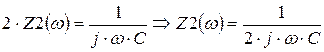 . (4.6)
. (4.6)
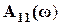 определяем с помощью (4.4) как обратный коэффициент передачи по напряжению в режиме ХХ относительно зажимов 2-2’ (рисунок 4.3,а). По закону Ома
определяем с помощью (4.4) как обратный коэффициент передачи по напряжению в режиме ХХ относительно зажимов 2-2’ (рисунок 4.3,а). По закону Ома
 (4.7)
(4.7)
 . (4.8)
. (4.8)
По той же схеме рисунка 4.3,а определяем 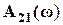
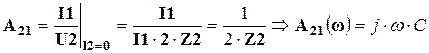 . (4.9)
. (4.9)
По схеме рисунка 4.3,б определяем 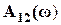 и
и 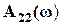 :
:
 ; (4.10)
; (4.10)
 (4.11)
(4.11)
 а)
а)
|  б)
б)
|
Рисунок 4.3
4.3 Исследование собственного затухания a и коэффициента фазы b
Указанные величины являются соответственно действительной и мнимой частью меры передачи g, определяемой в согласованном режиме выражением
 - (4.12)
- (4.12)
где 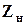 - сопротивление нагрузки;
- сопротивление нагрузки;
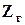 - эквивалентное внутреннее сопротивление источника сигнала;
- эквивалентное внутреннее сопротивление источника сигнала;
 ,
, 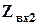 - входные сопротивления относительно зажимов 1-1' и 2-2' соответственно.
- входные сопротивления относительно зажимов 1-1' и 2-2' соответственно.
4.2.1. Рассмотрим Г-образный четырёхполюсник с Т-входом.Для определения выражений a(w) или b(w) получим для начала выражения для величины:
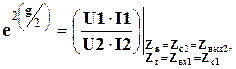 , (4.13)
, (4.13)
для Г-образного четырёхполюсника с Т-входом, где 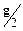 - обозначение меры передачи Г-четырёхполюсников, общепринятое для учебной и научно-технической литературы.
- обозначение меры передачи Г-четырёхполюсников, общепринятое для учебной и научно-технической литературы.
1) Определим соотношение между входными и выходными токами и напряжениями Г-четырёхполюсника с Т-входом в согласованном режиме (рисунок 4.4), то есть при
 . (4.14)
. (4.14)
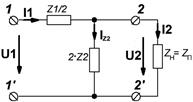
Рисунок 4.4 – Г-четырёхполюсник с Т-входом с согласованной нагрузкой
Приняв 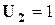 , получим:
, получим:
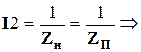 (4.15)
(4.15)

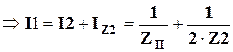 . (4.16)
. (4.16)
По закону Ома определяем падение напряжения на 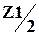
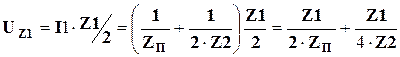 ,
,
а по второму закону Кирхгоффа – величину U1
 . (4.17)
. (4.17)
2) Определим отношение (4.13):
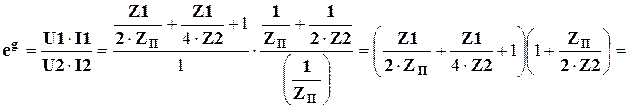
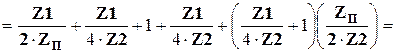
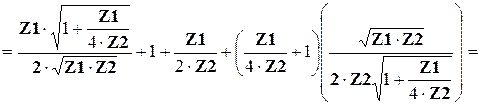 .
.

 . (4.18)
. (4.18)
4.2.2. Рассмотрим Г-образный четырёхполюсник с П-входом. Рассматриваемый четырёхполюсник (рисунок 4.5) является обратимым по отношению к предыдущему. Соответственно для них выполняются условия:
|
|
|
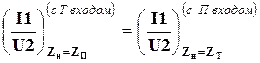 ,
, 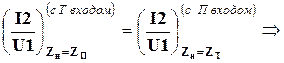

Þ для Г-образного четырёхполюсника справедливо выражение (4.18).

Рисунок 4.5 – Г-четырёхполюсник с Т-входом с согласованной нагрузкой
4.2.3. Мера передачи симметричных четырёхполюсников. Симметричные Т- и П-четырёхполюсники получаются каскадным соединением Г-образных четырёхполюсников с одинаковыми параметрами (рисунки 4.6,а и 4.6,б). Так правые Г-четырёхполюсники в приведённых на рисунках преобразованиях согласованы с генератором, левые – с нагрузкой, то между собой составные Г-четырёхполюсники также согласованы, и полученные Т- и П-четырехполюсники согласованы с нагрузкой и генератором, а для их мер передачи справедливо соотношение
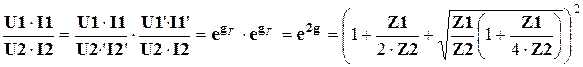 , (4.19)
, (4.19)
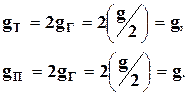 (4.20)
(4.20)
Таким образом, на основании выводов пунктов 4.2.2 и 4.2.3 можем заключить, для анализа меры передачи в ПП и в ПЗ для любого из рассмотренных четырёхполюсников, достаточно воспользоваться выражением (4.18).

а)

б)
Рисунок 4.6 – Симметричные четырёхполюсники
4.2.4. Анализ меры передачи в ПП и ПЗ. Так для реактивных фильтров и в ПП и в ПЗ должно выполняться второе условие неравенств (2.1), элементам Z1 и Z2 должны соответствовать реактивные сопротивления разного знака (реактивные элементы разного вида). То есть, если  , то
, то 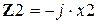 , и наоборот. Поэтому справедливо соотношение
, и наоборот. Поэтому справедливо соотношение
 , (4.21)
, (4.21)
а выражение (4.9) можно преобразовать к виду
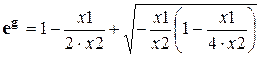 . (4.22)
. (4.22)
В ПП, согласно условиям (2.1), должно выполняться неравенство
 ,
,
соответственно, выражение (4.22) представляется в виде комплексного выражения
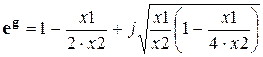 . (4.23)
. (4.23)
Определим модуль (4.14):

Þ в ПП мера затухания нулевая для фильтра любой структуры
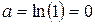 . (4.24)
. (4.24)
Для коэффициента фазы b в ПП выражение получим из (4.23):
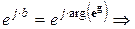
 . (4.25)
. (4.25)
Таким образом, подставив в (4.25) вместо x1 и x2 модули частотных зависимостей для | Z1(w)| и | Z2(w)|, полученные в подразделе 2.2, возможно получить зависимости b(ω) для проверки признаков ПП в строках 3 таблиц 2.3 или 2.4
В ПЗ, так как
 ,
,
то выражение (4.22) – чисто вещественное, и преобразуется к виду
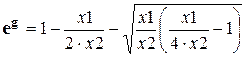 . (4.26)
. (4.26)
Поэтому выражение для меры затухания получим следующим макаром:

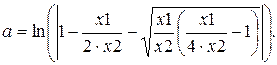 (4.27)
(4.27)
А коэффициент фазы будет принимать значения b=±π приотрицательных значения выражения (4.26), и b=0 – при положительных.
|
|
|
Таким образом, подставляя (4.27) в выражения в 3-х строках таблиц 2.3 и 2.4, проверим признаки ПЗ.
Заключение (выводы)
a) По построенным в пунктах 4, 5 раздела 2 диаграммам характеристических параметров сделать качественное заключение об их поведении в полосе пропускания.
b) Сравнить результаты определения границ полосы пропускания 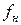 и
и 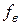 по критерию (2.1) и по уровню α= -3 дБ в пунктах 7 и 9 раздела 2 (если отличаются, указать относительное расхождение).
по критерию (2.1) и по уровню α= -3 дБ в пунктах 7 и 9 раздела 2 (если отличаются, указать относительное расхождение).
c) Аналогично сравнить границы полос пропускания, полученные теоретически по критерию (2.1) и по уровню α= -3 дБ по экспериментальным диаграммам ЛАЧХ в трёх режимах (если отличаются, указать, на сколько процентов отличается каждая граничная частота).
d) По полученным аналитическим диаграммам ЛАЧХ в режиме ХХ и в нагруженном режиме сделать экспертное заключение о качестве фильтрации в каждом режиме по следующим критериям:
1) по степени неравномерности в полосе пропускания (определённой по уровню α)
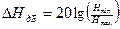
где 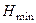 ,
,  - минимальное и максимальное значение АЧХ в полосе пропускания;
- минимальное и максимальное значение АЧХ в полосе пропускания;
2) по скорости затухания ЛАЧХ за пределами полосы пропускания (в течение первых октав после граничных частот, вторых октав, третьих, в течение вторых декад)*.
Правила оформления отчёта
a) Оформлять работу в электронном виде в программной среде MatchCad или MicrosoftWord, согласно правилам оформления расчётно-графических работ, рефератов или отчётов по практике, указанным в приложениях Ц или Ю в [2].
b) На второй странице (после титульного листа) – цель лабораторной работы и схема фильтра.
c) Все требуемые результаты аналитических расчётов, объём пояснений хода вычислений – по степени надобности самому студенту, все требуемые диаграммы из программной среды MathCad.
d) По экспериментальной части – таблица приложения B.
e) Таблица A.1 и выводы.
Литература, рекомендуемая для изучения темы
7.1 Бессонов, Л. А. Теоретические основы электротехники. Электрические цепи: учебник / Л.А. Бессонов- 11-е изд., испр. и доп. – М.: Гардарики, 2007. - 701 с. - ISBN 5-8297-0159-6.
|
|
|
7.2 Прянишников, В. А. Теоретические основы электротехники: Курс лекций / В.А. Прянишников.- 3-е изд., перераб. и доп. - СПб.: Корона принт, 2000. – 368 с.: ил. - Библиогр.: с. 366. - ISBN 5-7931-0104-7.
7.3 Матханов, П. Н. Основы анализа электрических цепей: линейные цепи: учеб. для вузов / П. Н. Матханов.- 3-е изд., перераб. и доп. - М.: Высш. шк., 1990. - 400 с.: ил. - ISBN 5-06-000679-4.
7.4 Зевеке, Г. В. Основы теории цепей / Г. В. Зевеке, П. A. Ионкин, А.В. Нетушил, С.В. Страхов.- 4-е изд., перераб. - М.: Энергия, 1975. - 752 с.: ил.
7.5 Нейман, Л. Р. Теоретические основы электротехники: в 2 т.: учеб. для вузов / Л. Р. Нейман, К. С. Демирчян. - 3-е изд., перераб. и доп. - Л.: Энергоиздат, 1981. - Т.1. - 536 с.: ил.
|
|
|


