 |
Построение графиков функций в полярной системе координат
|
|
|
|
 | |||
 | |||
Рисунок 19
Полярная система координат на плоскости — это совокупность точки 
, называемой полюсом, и полупрямой 
, называемой полярной осью.
Положение точки M в полярной системе координат определяется расстоянием r (полярным радиусом) от точки M до полюса и углом j (полярным углом) между полярной осью и вектором 
. (рисунок 19).
Полярный радиус и полярный угол составляют полярные координаты точки M, что записывается в виде M (r,j). Полярный угол измеряется в радианах и отсчитывается от полярной оси:
- в положительном направлении (против направления движения часовой стрелки), если значение угла положительное;
- в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.
Связь между декартовыми и полярными координатами
Пару полярных координат r и j можно перевести в Декартовы координаты x и y по следующим фомулам:
Обратно, полярный радиус r можно найти, зная декартовы координаты x и y, по теореме Пифагора (см. Рис.??):
,
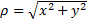а полярный угол j в диапазоне [0, 2p), находится при помощи обратной (к тангенсу) тригонометрической функции арктангенс:
Пример № 2. Построить график функции r(j) = 2.
1. Задаём значения j в градусах в диапазоне [0, 2p] с шагом в 5 градусов с использованием автозаполнения (см. Приложение 1).
2. Перевести j из градусов в радианы с использованием функции РАДИАНЫ (см. Приложение 2).
3. Рассчитать значения r(jрад).
4. По значениям jрад и r(jрад) рассчитать декартовы координаты x и y.
5. По рассчитанным значениям x и y построить график, выбрав тип диаграммы Точечная.
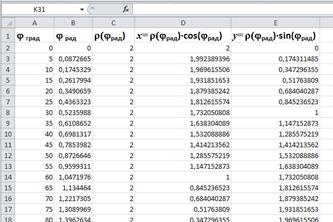
Рисунок 20. Результаты расчёта
Рисунок 21. График функции r(j) = 2
|
|
|
Задание № 4
С помощью пакета Microsoft Excel построить график функций, приведенные в Приложении 5 соответственно варианту. Порядок расчета и результат оформить в виде отчета, содержащего следующие пункты:
a. Первый лист: Титульный лист – пример оформления см в приложении 6,
b. Привести текст задания,
c. Привести расчётные формулы и результаты расчёта,
d. График построенной функции,
e. Указать полярные координаты точки графика, заданной преподавателем.
Построение графиков функций с использованием логарифмической шкалы.
|
|
Рисунок 22
Логарифмическая шкала исключительно удобна для отображения очень больших диапазонов значений величин.
Пример № 3. Построить график функции 
. в диапазоне значений [-5, 5] и определить по графику значение функции для х = -3.6 и х = 4.
1. Задаём значения х в диапазоне [-5, 5] с шагом 0.5 с использованием автозаполнения (см. Приложение 1).
2. По заданным х рассчитываем значения функции у.
3. Строим график функции, используя тип диаграммы «точечная» и замечаем, например,что значение функции при отрицательных х очень близко к 0, так что определить его из графика не представляется возможным
Рисунок 23
4. Выделяем ось у.
5. Делаем щелчок правой кнопкой мыши и в раскрывшемся контекстном меню выбираем «формат оси» (см. рисунок 12)
6. В окне «формат оси» помечаем галочкой логарифмическую шкалу.
7. Добавить основные и промежуточные линии сетки.
Результаты представлены на Рисунке 24
|
|
|
Рисунок 24
Из рисунка определяем, что для х = -3.6 значение 
примерно равно 0.02, а для х = 4 
.
6.1.Задание № 5. Построить график функций 
в диапазоне значений [-10, 10] с шагом 0.5. Уметь из графика определять значение функции для указанного (преподавателем) аргумента. Порядок расчета и результат оформить в виде отчета, содержащего следующие пункты:
a. Первый лист: Титульный лист – пример оформления см в приложении 6,
b. Привести текст задания,
c. Привести графики без использования логарифмической шкалы,
d. Привести графики с использованием логарифмической шкалы,
e. Сравнить результаты.
|
|
|
