 |
Принцип компенсации напряжения
|
|
|
|
Принцип компенсации напряжения основан на теореме о компенсации, которая гласит: в любой электрической цепи без изменения токов в ее ветвях сопротивление в произвольной ветви можно заменить источником с ЭДС, численно равной падению напряжения на этом сопротивлении и действующей навстречу току в этой ветви.
Потенциальная диаграмма.
Под потенциальной диаграммой понимается график распределения потенциала вдоль какого-нибудь участка цепи замкнутого контура.
По оси абсцисс откладывают сопротивления вдоль контура, начиная с какой-либо произвольной точки, по оси ординат – потенциалы.
Каждой точке участка цепи или замкнутого контура соответствует своя точка на потенциальной диаграмме.
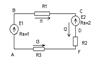
Пример: Составить потенциальную диаграмму для контура изображенного на рис. (предполагается, что величины и направления токов определены).
Произвольно выбирается потенциал какой-либо точки, равный нулю. Допустим точки a, то есть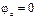 
. Тогда потенциал точки b определяется:
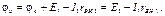Потенциалы остальных точек контура
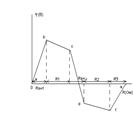
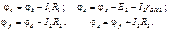
Потенциальная диаграмма для данного контура представлена на рис.
Полученная диаграмма позволяет просто определить напряжение между двумя любыми точками контура, так как напряжение есть разность потенциалов 
где: 
– потенциал точки высшего напряжения,
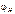– потенциал точки низшего напряжения.
15.Баланс мощностей является следствием закона сохранения энергии — суммарная мощность вырабатываемая (генерируемая) источниками электрической энергии равна сумме мощностей потребляемой в цепи.Баланс мощностей используют для проверки правильности расчета электрических цепей. 
Преимущества цепей переменного тока. Способы представления синусоидальных токов, напряжений, ЭДС
|
|
|
При расчете и анализе электрических цепей применяют несколько способов представления синусоидальных электрических величин.
Тригометрический способ
Для тока
(2.1)
i(t) = Im sin(ωt + ψi),
для напряжения
(2.2)
u(t) = Um sin (ωt +ψu),
для ЭДС
(2.3)
e(t) = Em sin (ωt +ψe),
В уравнениях (2.1 – 2.3) обозначено:
Im, Um, Em – амплитуды тока, напряжения, ЭДС;
значение в скобках – фаза (полная фаза);
ψi, ψu, ψe – начальная фаза тока, напряжения, ЭДС;
ω – циклическая частота, ω = 2πf;
f – частота, f = 1 / T; Т – период.
Величины i, Im – измеряются в амперах, величины U, Um, e, Em – в вольтах; величина Т (период) измеряется в секундах (с); частота f – в герцах (Гц), циклическая частота ω имеет размерность рад/с. Значения начальных фаз ψi, ψu, ψe могут измеряться в радианах или градусах. Величина ψi, ψu, ψe зависит от начала отсчета времени t = 0. Положительное значение откладывается влево, отрицательное – вправо.
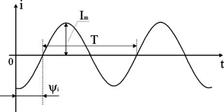
Временная диаграмма
Временная диаграмма представляет графическое изображение синусоидальной величины в заданном масштабе в зависимости от времени (рис. 2.1).
i(t) = Im sin(ωt - ψi).
Графоаналитический способ
Графически синусоидальные величины изображаются в виде вращающегося вектора (рис. 2.2). Предполагается вращение против часовой стрелки с частотой вращения ω. Величина вектора в заданном масштабе представляет амплитудное значение. Проекция на вертикальную ось есть мгновенное значение величины
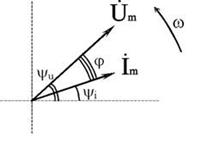Совокупность векторов, изображающих синусоидальные величины (ток, напряжение, ЭДС) одной и той же частоты называют векторной диаграммой.
Использование векторных диаграмм позволяет существенно упросить анализ цепей переменного тока, сделать его простым и наглядным.
В основе графоаналитического способа анализа цепей переменного тока лежит построение векторных диаграмм.
|
|
|
Представление с использованием комплексных чисел
|
|
|
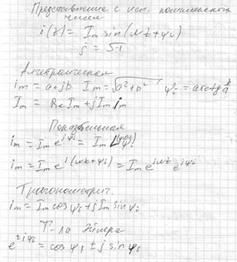
