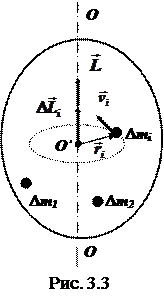|
Момент инерции тела относительно оси
|
|
|
|

|
Пусть имеется твердое тело. Выберем некоторую прямую ОО (рис.3.1), которую будем называть осью (прямая ОО может быть и вне тела). Разобьем тело на элементарные участки (материальные точки) масссами Δ m  , Δ m
, Δ m 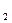 ,..., Δ m
,..., Δ m 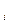 , находящиеся от оси на расстоянии соответственно r
, находящиеся от оси на расстоянии соответственно r  , r
, r 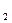 ,... r
,... r  .
.
Моментом инерции материальной точки относительно оси OO называется произведение массы материальной точки на квадрат ее расстояния до этой оси:
D Ii = D mi  ri2. (3.1)
ri2. (3.1)
Моментом инерции (МИ) тела относительно оси ОО называется сумма произведений масс элементарных участков тела на квадрат их расстояния до оси:
 I =
I = 
 . (3.2)
. (3.2)
Как видно, момент инерции тела есть величина аддитивная - момент инерции всего тел относительно некоторой оси равен сумме моментов инерции отдельных его частей относительно той же оси.
В данном случае
 .
.

Измеряется момент инерции в кг·м  .
.
Так как
D mi = r D Vi, (3.3)
где ρ - плотность вещества; D Vi - объем i - го участка, то  или, переходя к бесконечно малым элементам,
или, переходя к бесконечно малым элементам,
I =  . ( 3.4)
. ( 3.4)
Формулу (3.4) удобно использовать для вычисления МИ однородных тел правильной формы относительно оси симметрии, проходящей через центр масс тела. Например, для МИ цилиндра относительно оси, проходящей через центр масс параллельно образующей, эта формула дает
 ,
,
где m - масса; R - радиус цилиндра.
Большую помощь при вычислениях МИ тел относительно некоторых осей оказывает теорема Штейнера: МИ тела I относительно любой оси равен сумме МИ этого тела Iс относительно оси, проходящей через центр масс тела и параллельно данной, и произведения массы тела на квадрат расстояния d между указанными осями:
I = Iс+ m d2. (3.5)
Момент силы относительно точки и оси
|
|
|
 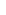     
|
Пусть на тело действует сила  . Примем для простоты, что сила
. Примем для простоты, что сила  лежит в плоскости, перпендикулярной некоторой прямой ОО (рис.3.2), которую назовем осью (например, это ось вращения тела). На рис. 3.2
лежит в плоскости, перпендикулярной некоторой прямой ОО (рис.3.2), которую назовем осью (например, это ось вращения тела). На рис. 3.2
А - точка приложения силы  ; О΄ - точка пересечения оси с плоскостью, в которой лежит сила; А относительно точки О΄;
; О΄ - точка пересечения оси с плоскостью, в которой лежит сила; А относительно точки О΄; 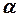 - угол между
- угол между 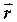 и
и  .
.
Моментом силы  относительно точки О΄ называется вектор
относительно точки О΄ называется вектор 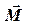 (псевдовектор), определяемый равенством
(псевдовектор), определяемый равенством
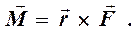 (3.6)
(3.6)
Модуль этого вектора
M = F  r
r  sin a. (3.6, а)
sin a. (3.6, а)
Величина b = r  sin a называется плечом силы (кратчайшее расстояние от точки О΄ до линии действия силы).
sin a называется плечом силы (кратчайшее расстояние от точки О΄ до линии действия силы).
Моментом силы относительно оси ОО называется скалярная величина М00, равная проекции на эту ось вектора 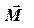 момента силы, определенного относительно точки О΄, лежащей на данной оси.
момента силы, определенного относительно точки О΄, лежащей на данной оси.
В нашем случае
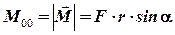 . (3.7)
. (3.7)
В соответствии с выражениями (3.6) и (3.7) вектор  направлен по оси ОО, а его проекция М00 лежит на этой оси (cм. рис.3.2).
направлен по оси ОО, а его проекция М00 лежит на этой оси (cм. рис.3.2).
Момент импульса тела относительно оси вращения
Пусть тело вращается вокруг некоторой оси ОО с угловой скоростью ω. Разобьем это тело мысленно на элементарные участки с массами D m1, D m2,... D mi,..., которые находятся от оси соответственно на расстояниях D r1, D r2,... , D r3 ,...,  и вращаются по окружностям, имея линейные скорости v1, v2,..., vi,.... Известно, что величина, равная
и вращаются по окружностям, имея линейные скорости v1, v2,..., vi,.... Известно, что величина, равная 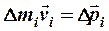 - есть импульс i - го участка. Моментом импульса i - го участка (материальной точки) относительно точки О΄ называется вектор (псевдовектор)
- есть импульс i - го участка. Моментом импульса i - го участка (материальной точки) относительно точки О΄ называется вектор (псевдовектор)
 , (3.8)
, (3.8)
где 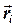 - радиус-вектор, определяющий положение i -го участка относительно точки О΄.
- радиус-вектор, определяющий положение i -го участка относительно точки О΄.
Моментом импульса всего тела относительно точки О΄ называют вектор: 
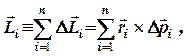 (3.9)
(3.9)
модуль которого
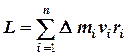 . (3.9, а)
. (3.9, а)
Моментом импульса тела относительно неподвижной оси ОО называется скалярная величина L00, равная проекции на эту ось вектора  момента импульса тела, определенного относительно точки О΄, лежащей на данной оси.
момента импульса тела, определенного относительно точки О΄, лежащей на данной оси.
|
|
|
|
В соответствии с выражениями (3.8) и (3.9) векторы  и
и 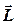 направлены по оси ОО (рис.3.3). Легко показать, что момент импульса тела L00 относительно оси ОО и момент инерции I этого тела относительно той же оси связаны соотношениями
направлены по оси ОО (рис.3.3). Легко показать, что момент импульса тела L00 относительно оси ОО и момент инерции I этого тела относительно той же оси связаны соотношениями
 , L00=I· ω. (3.10)
, L00=I· ω. (3.10)
|
|
|