Краткие теоретические сведения

Физическим маятником (ФМ) называется твердое тело, которое может колебаться под действием силы тяжести вокруг горизонтальной оси (не проходящей через центр масс тела).

При колебании ФМ вращается вокруг оси, перпендикулярной плоскости рисунка и про­хо­дя­щей через точку О (рис. 4.1). Эта точка назы­ва­ет­ся точкой подвеса. Движение маятника подчиня­ет­ся основному уравнению динамики враща­тель­но­го движения:

 

или М = I e, (4.1)

 

где М - момент силы тяжести относительно оси О; I - момент инерции маятника относительно той же оси; - угловое ускорение маятника.

Из рис. 4.1 видно, что

 

М = - mgb sin j, (4.2)

 

где m - масса маятника; b sin j - плечо силы тяжести mg; b - расстояние от точки подвеса О до центра масс С.

Знак “-” означает, что вращающий момент М стремится уменьшить угол j, характеризующий отклонение маятника от равновесного положения. Более строго смысл знака “-” объясняется так: псевдовекторы момента сил и смещения от положения равновесия направлены в противоположные стороны (для ситуации, изображенной на рис. 4.1 первый направлен за плоскость чертежа, а второй - из этой плоскости на наблюдателя). Помня, что , и учитывая (4.1), уравнение (4.2) запишем в виде

. (4.3)

 

При малых отклонениях маятника (именно этот случай мы и будем иметь в виду) sin j » j, а потому равенство (4.3) после деления на I примет вид

 

(4.4)

 

Положительная величина mgb/I может быть заменена квадратом некоторого числа:

m g b / I º w ₀². (4.5)

 

Тогда уравнение (4.4) можно переписать как

 

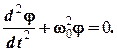(4.6)

 

Используя прямую подстановку, убеждаемся, что решением уравнения (4.6) является выражение

j = j ₀ cos ( w ₀ t + a ). (4.7)

 

Это свидетельствует о том, что ФМ совершает в этих условиях незатухающие гармонические колебания с циклической частотой w₀. Амплитуда и начальная фаза j ₀ и a – постоянные, зависящие от начальных условий.

Период колебаний ФМ

 

(4.8)

 

Величина I / mb имеет размерность длины, обозначим ее L и назовем приведенной длиной ФМ:

L = I / m b. (4.9)

Таким образом,

(4.10)

 

Сравнивая (4.10) с формулой для периода колебаний математического маятника T = 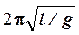, где l - длина математического маятника, видим, что приведенная длина ФМ - это длина такого математического маятника, у которого период колебаний совпадает с периодом колебаний данного ФМ. Легко заметить, что L > b. В самомделе, в соответствии с теоремой Штейнера I = I_с + mb², где I_c - момент инерции маятника относительно оси, проходящей через центр масс. Следовательно, по выражению (4.9)

 

(4.11)

 

откуда видно, что L>b.

Точку О΄ (см. рис. 4.1), отстоящую от О на расстоянии L, называют точкой качаний.

 

Описание установки и метода определения момента инерции

Исследуемое тело 1 пред­ста­вляет собой металлическую пла­сти­ну с двумя вырезами (рис. 4.2). Эти­ми вырезами тело подвешивается на опору - кронштейн 2 для орга­ни­за­ции ко­ле­ба­ний. Чтобы уменьшить тре­ние и износ детали точки под­ве­са О₁ и О₂ сна­бжены специальными под­­став­ка­ми 3. На конце крон­штей­на мо­жет быть подвешен мате­мати­чес­­кий ма­ят­ник 4, длину которого мож­но изменять.

В работе определяются мо­мен­ты инерции I₁ и I₂ относительно осей О₁ и О₂. Метод определения мо­мен­тов инерции основан на том, что пе­ри­од колебаний ФМ связан с его мо­мен­том инерции относительно оси колебания (см. формулу (4.8)). Таким образом, измерив на опыте период колебаний маятника Т и расстояние b от точки подвеса до центра масс (см. рис.4.1), зная массу m маятника и ускорение свободного падения g, можно вычислить момент инерции:

 

(4.12)

Порядок выполнения работы

 

1. Снять пластину с подвеса, измерить линейкой расстояния b₁ = O₁C и b₂ = O₂C (см. рис.4.2) и оценить ошибку D b этих измерений. Результаты занести в табл. 4.1; сюда же вписать данные о массе тела и ускорении свободного падения.

2. Подвесить маятник на ось О₁, привести его в движение (j £ 8^о) и измерить время t₁ для 30-50 полных колебаний N. (Отсчет времени лучше начинать после того, как тело совершит несколько колебаний). Опыт повторить не менее 5 раз при одном и том же числе колебаний. Результаты (эти и последующие) занести в табл. 4.1.

Таблица 4.1

 

№	Число полн.	Колебания на оси О1	Колебания на оси О2
п/п	колеб. N	t1 , с	Т1, с	t2, с	T2, с	(T2i - <T2>), с	(T2i - <T2>)2, с2
. . .
Другие b1 = ± m = ± L1 = данные b2 = ± g = ± L2 =

 

3. Снять маятник и, подвесив его на ось О₂, проделать тоже, что и в п.2.

4. Вычислить периоды колебаний Т₁ и Т₂ для каждого из опытов и их средние значения <T₁> и <T₂>.

5. По формуле

 

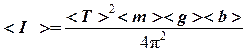
(см. (4.12)) вычислить <I₁> и <I₂>.

6. Для момента инерции I₂ вычислить относительную погрешность e _I2 (для I₁ принять ее такой же). Для этого:

а) подсчитать Т_2i - <Т₂>, (T_2i - <T₂>)², 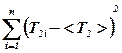(cм. табл. 4.1);

б) вычислить абсолютную погрешность в измерении периода колебаний

,

 

где n - число измерений; N – число выбранных колебаний; D t_пр - приборная погрешность секундомера; t_{a,n -} коэффициент Стьюдента (определяется по таблице в зависимости от выбранной надежности a и n);

в) определить относительную погрешность

 

.

 

7. Вычислить абсолютные погрешности в определении моментов инерции:

D I₁ = e _I <I₁>, D I₂ = e _I <I₂>.

8. Результаты представить в виде:

 

I₁ = <I₁> ± D I₁ , I₂ = <I₂> ± D I₂ при a = …, e _I = … %.

 

9. Вычислить приведенные длины L₁ и L₂ маятников по формуле

 

 

10. При наличии математического маятника установить его длину l равной L₁ (или L₂) и убедиться в синхронности колебаний физического и математического маятников.

 

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Физический маятник.

2. Уравнения колебаний физического маятника (дифференциальное уравнение и его решение).

3. Частота и период колебаний физического маятника.

4. Приведенная длина физического маятника.

5. Точка подвеса и центр качаний физического маятника.

6. Метод определения I в данной работе.

7. Порядок выполнения работы.

 

 

ЛАБОРАТОРНАЯ РАБОТА № 5

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: