 |
Вычисление определенного интеграла по общей формуле Симпсона
|
|
|
|
Национальный горный университет
 |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КУРСОВОЙ РАБОТЕ
по нормативной дисциплине “Информатика” (C++)
Направление подготовки – «Телекоммуникация»
Днепропетровск
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
Национальный горный университет
 |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КУРСОВОЙ РАБОТЕ
по нормативной дисциплине “Информатика” (C++)
Направление подготовки «Телекоммуникация»
Днепропетровск
Цель работы
Целью курсовой работы является закрепление знаний и умений программирования на языке C/C++ при создании реального действующей программы
1. Наименование работы: «Численные методы решения математических задач с использованием языка программирования С++»
2. Требования к курсовой работе
Курсовая работа должна содержать:
1. Пояснительную записку.
2. Задание.
3. Описание заданных методов.
4. Схему алгоритма.
5. Программу на языке программирования С++.
6. Файлы с результатами работы программы.
7. Выводы.
2.1. Содержание пояснительной записки:
· Титульный лист.
· Задание к курсовой работе.
· Содержание пояснительной записки.
· Блок-схемы программ.
· Исходные тексты программ.
· Содержание файлов с результатами работы программы.
· Выводы.
· Список использованной литературы
Образец титульного листа приведён в приложении 1, а образец задания в приложении 2.
2.2. Требования к программам
Программы должны являться самостоятельными и независимыми программными единицами, разработанными на языке программирования C/C++.
3. Варианты заданий к курсовой работе выбирать следующим обазом:
|
|
|
– решение алгебраических и трансцендентных уравнений [табл.1]
– нахождение определенных интегралов [табл.2]
ЗАДАНИЕ 1: Решение алгебраических и трансцендентных уравнений.
Методические указания.
Рассмотрим некоторые методы решения уравнений вида
f(x)=0 (1),
где функция f(x) определена и непрерывна на некотором числовом множестве Х.
Корни достаточно сложных алгебраических и трансцендентных уравнений очень редко можно определить точными методами. Если же коэффициенты таких уравнений являются приближенными числами (например, определяются экспериментально), то задача о точном определении корней вообще не может быть поставлена. Поэтому на практике уравнения вида (1) часто решают приближенными методами (напомним, что корнем называется всякое число, обращающее функцию f(x) в нуль).
При использовании данных методов корень уравнения вычисляется с некоторой степенью точности ع, т.е. если ξ –корень уравнения,. а х – его приближенное значение, то должно выполняться условие
| ξ - х | ≤ ع
Задача определения корней уравнения (1) включает в себя два этапа:
· отделение корней, т.е. определение как можно более узкого отрезка [ a;b] на котором имеется только один корень;
· уточнение корней, т.е. доведение их приближенных значений до требуемой степени точности.
Процесс отделения корней проводится в соответствии с физическим смыслом задачи графически или с помощью таблицы значений функции f(x), если,. конечно такая таблица имеется. Обычно используют графический способ. Очевидно, что точность определения области существования корня таким образом будет невелика,. однако эти значения будут уточнены на втором этапе решения.
Прежде чем приступить к рассмотрению методов приближенного решения уравнения отметим, что если функция f(x) на концах отрезка [ a;b] принимает значения разных знаков, а ее производная в этом интервале не меняет знак, то в данном интервале имеется только один корень уравнения.
|
|
|
Метод половинного деления
Построив график функции f(x) и определив отрезок [a;b], на котором лежит корень уравнения (рис. 1),. можно уточнить его значение методом половинного деления.
Метод заключается в последовательном уменьшении отрезка [a;b], вдвое для этого определяем значения f(а) и f(b), которые должны иметь разные знаки, делим отрезок пополам и вычисляем значение f(с), где
с=(а+b)/2
Если при этом f(c) = 0, то с – корень уравнения. Если же f(c) ≠ 0, то из двух отрезков [a;с] и [с;b] выбираем тот, на концах которого функция f(x) имеет значения разных знаков, т.к. только на этом отрезке может находиться
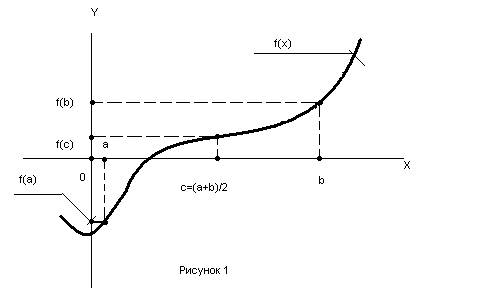
корень уравнения. Для нашего примера таким отрезком будет [a;с]. Обозначив его [a1;b1], последовательно определяем с1=(а1+b1)/2, f(c1) и проводим аналогичные рассуждения.
В результате таких «половинных делений» получим ряд отрезков [a1;b1], [a2;b2], [a3;b3], …, [ai;bi], …, [an;bn], каждый из которых удовлетворяет условию
f(аi) f(bi)<0,

Вычислительный процесс окончится в том случае, если выполнится условие f(сi)=0, т.е. будет найдено точное значение корня (что на практике встречается редко), или же получится отрезок [ai;bi] для которого выполнится условие
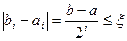 , где
, где  – заданная точность вычисления корня (погрешность вычислений).
– заданная точность вычисления корня (погрешность вычислений).
Метод итераций (метод последовательных приближений)
Запишем уравнение f(х)=0, для которого должен быть определен интервал изоляции в [a;b] виде:
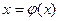 (2)
(2)
Если при этом во всех точках отрезка в [a;b] выполняется условие
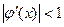 (3),
(3),
то итерационный процесс сходится к искомому корню.
Метод итераций заключается в следующем: выбираем начальное значение корня х0 (любую точку принадлежащую интервалу изоляции) и подставляем его в правую часть уравнения (2), т.е. определяем 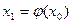 . Затем в уравнение (2) подставляем найденное значение х1, получая
. Затем в уравнение (2) подставляем найденное значение х1, получая 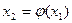 и т. д.
и т. д.
Если в качестве начального приближения х0 принять одну из границ отрезка [a;b], например а, то процесс уточнения корня методом итераций можно представить следующей схемой:
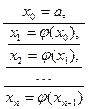
Таким образом, каждое новое приближение определяется по формуле:

где n=11,2,…
Процесс вычислений по рассмотренной выше схеме продолжаем до тех пор, пока не выполнится условие
|
|
|
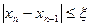 ,
,
где  – заданная точность вычисления корня.
– заданная точность вычисления корня.
В том случае, если условие (3) не выполнилось, т.е. если  , процесс будет расходиться и уравнение вида (1), следовательно, не может быть решено методом итераций.
, процесс будет расходиться и уравнение вида (1), следовательно, не может быть решено методом итераций.
Чтобы получить сходящийся итерационный процесс, над уравнением (1) необходимо выполнить равносильные преобразования – умножим обе части уравнения на некоторое число 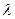 , а затем прибавим к обеим частям полученного уравнения
, а затем прибавим к обеим частям полученного уравнения 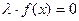 х:
х:
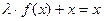 (4)
(4)
Обозначив левую часть уравнения (4) как 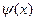 , т.е.
, т.е. 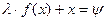 , запишем это уравнение в виде:
, запишем это уравнение в виде:
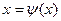 (5)
(5)
Таким образом, мы привели уравнение (4), равносильное уравнению (1), к виду, удобному для применения метода итераций.
Число 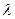 , входящее в уравнение (5), выбираем таким, чтобы в интервале [a;b] выполнялось условие (3), т.е.
, входящее в уравнение (5), выбираем таким, чтобы в интервале [a;b] выполнялось условие (3), т.е. 
Очевидно, что это выражение можно записать в виде
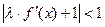
Подобрав значения  , подставляем его в уравнение (4) и решаем это уравнение по рассмотренной выше схеме.
, подставляем его в уравнение (4) и решаем это уравнение по рассмотренной выше схеме.
Примечание:
· при реализации программы методами половинного деления или итераций на С++ вычисление f(x) целесообразно оформить в виде функции;
· для определения участка на котором существует корень функции следует использовать математический пакет MathCad.
Метод хорд
Пусть дано уравнение f(x)=0, где f(x) – непрерывная функция, имеющая в интервале [a,b] производные первого и второго порядков. Корень считается отделенным и находится наа отрезке [a,b], т.е. f(a)∙f(b)<0.
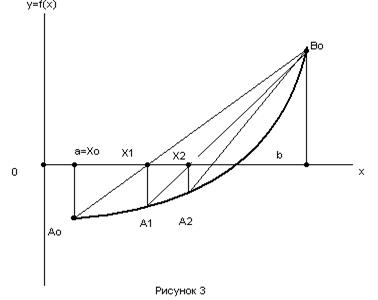
Идея метода хорд состоит в том, что на достаточно малом отрезке [a,b] дуга кривой y=f(x) (рис. 3) заменяется стягивающей ее хордой. В качестве приближенного значения корня принимается точка Х1 пересечения хорды с осью 0Х.
Рассмотрим случаи, когда первая и вторая производные имеют одинаковые знаки, т.е.  .
.
Пусть, например,  ,
, 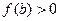 ,
, 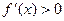 ,
, 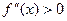 . График функции проходит через точки A0(a,f(a)), B0(b,f(b)).
. График функции проходит через точки A0(a,f(a)), B0(b,f(b)).
Искомый корень уравнения f(x)=0 есть абсцисса точки пересечения графика функции y=f(x) с осью 0Х. эта точка пока неизвестна, но вместо нее мы возьмем точку Х1 пересечения хорды A0B0 с осью 0Х. Это и будет приближенное значение корня.
|
|
|
Уравнение хорды, проходящей через точки A0 и B0 имеет вид:
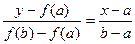
Найдем значение Х=Х1, для которого Y=0:

Эта формула называется формулой метода хорд. Теперь корень уравнения находится внутри отрезка [x1,b]. Соединим точку А1(x1,f(x1)) с точкой B(b,f(b)) и найдем Х2 – точку пересечения хорды А1В с осью 0Х:
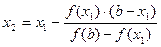
Продолжая процесс, находим

и вообще

Процесс продолжается до тех пор, пока мы не получим приближенный корень с заданной точностью, т.е.  .
.
По выше приведенным формулам вычисляются корни и для случая, когда 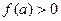 ,
, 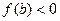 ,
, 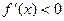 ,
,  (рис. 4).
(рис. 4).
Теперь рассмотрим случаи, когда первая и вторая производные имеют разные знаки, т.е. 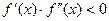 (рис. 5).
(рис. 5).
Пусть, например,  ,
, 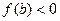 ,
, 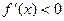 ,
, 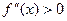 .
.
Соединим точки Ао(a, f(a)) и Bo(b, f(b)) и запишем уравнение хорды, проходящей через Ао и Bo:

Найдем x1 как точку пересечения хорды с осью ОХ, полагая y=0:
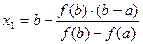
Теперь корень заключен внутри отрезка [a, x1].
Применяя метод хорд к отрезку [a,x1]., получим

и вообще
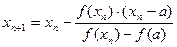
По этим же формулам находится приближенное значение корня и для случая, когда  ,
, 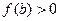 ,
, 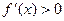 ,
,  (рис. 6).
(рис. 6).
Выбор формул можно осуществить, пользуясь правилом: неподвижным концом отрезка является тот, для которого знак функции совпадает со знаком второй производной.
Варианты заданий:
| № варианта | алгебраические уравнения | трансцендентные уравнения |
| 1. | 6x3-5x2-3x+8=0 | 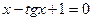
|
| 2. | 10х4-15х+8=0 | 
|
| 3. | 1х4-15х3+8х2-5х+4=0 | 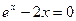
|
| 4. | 1х5-8х3+х2+3х-8=0 | 
|
| 5. | 5х3+8х2-20х+3=0 | 
|
| 6. | 7х3+5х2-13=0 | 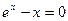
|
| 7. | 5х2+12х-13=0 | 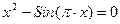
|
| 8. | 3х4+7х3+50х2+26х+4=0 | 
|
| 9. | 4х4+15х-13=0 | 
|
| 10. | 3х3+18х-16=0 | 
|
| 11. | 13х3-6х2+19х-18=0 | 
|
| 12. | 1х4-12х3-18=0 | 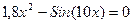
|
| 13. | 6х3-7х2+4=0 | 
|
| 14. | 3х3+10х-19=0 | 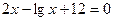
|
| 15. | 8х8-15х7-16х3-19=0 | 
|
| 16. | 3х3-12х2+12х-8=0 | 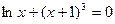
|
| 17. | 5х5-10х-2=0 | 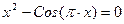
|
| 18. | 8х3-14х-12=0 | 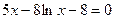
|
| 19. | (4х2-5)*(1-х3)=0 | 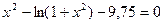
|
| 20. | 1х4-9х2-7х+3=0 | 
|
| 21. | 1х4-9х2-7х+3=0 |  
|
| 22. | 2х6-8х4+3х3-х+2=0 | 
|
| 23. | 2х3-8х2-16х+15=0 | 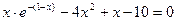
|
| 24. | 12х4-16х3+2х-3=0 | 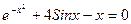
|
| 25. | 4х5-12х3-5х+2=0 | 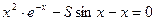
|
| 26. | 1,8х7+2х5-1,5х3+8х-4=0 | 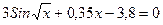
|
| 27. | 13х3-6х2+19х-18=0 | 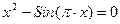
|
| 28. | 3х3-12х2+12х-8=0 | 
|
| 29. | 2х3-8х2-16х+15=0 | 
|
| 30. | 5х3+8х2-20х+3=0 | 
|
ЗАДАНИЕ 2: Нахождение определенных интегралов, заданными методами с использованием языка программирования С++.
1.Составить схему алгоритма для вычисления определенного интеграла (табл.2) при 8–10 значениях
Методические указания.
.
Вычисление определенного интеграла по общей формуле Симпсона
Требуется вычислить интеграл:
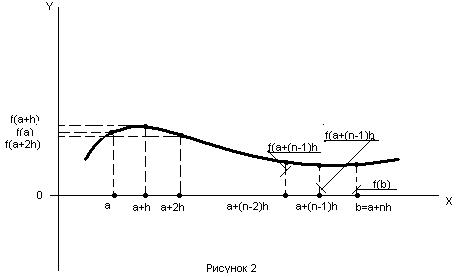
 (1)
(1)
Здесь a и b соответственно нижний и верхний пределы интегрирования; f(x)– подынтегральная функция, заданная аналитически.
Размер участка интегрирования
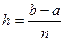 (2)
(2)
где n – число участков интегрирования, четное число. Общая формула Симпсона может быть представлена в виде
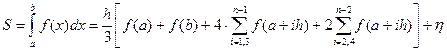 (3)
(3)
Формулу (3) можно преобразовать к виду с одной суммой
 (4)
(4)
|
|
|
Погрешность усечения
 ,
,  ?[a,b] (5)
?[a,b] (5)
По формулам (3) и (4) можно вычислить интеграл S, а по (5) – оценить погрешность вычислений. Если же потребуется вычислить интеграл с заданной точностью 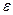 , то необходимо определить шаг интегрирования h или, что то же самое, число участков интегрирования n обеспечивающих требуемую точность.
, то необходимо определить шаг интегрирования h или, что то же самое, число участков интегрирования n обеспечивающих требуемую точность.
Можно поступить двояко:
· использовать выражение для погрешности усечения (5).
Находим такое число М, что
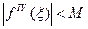 (6)
(6)
В этом случае
 (7)
(7)
Если потребовать, чтобы
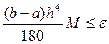 , то при
, то при
 (8)
(8)
будет получена требуемая точность вычисления.
Пример. Определить шаг интегрирования для вычисления интеграла  с
с  ; y=Sinx; yIVSsinx;
; y=Sinx; yIVSsinx;  ; M=1
; M=1
a=0; b=π.

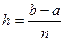 ;
; 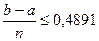 ;
; 
Выбираем 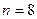 .
.
В тех случаях, когда оценка значений четвертой производной подынтегральной функции затруднительна,. применяют способ двойного пересчета;
· использовать способ двойного пересчета.
Вычисляют интеграл S дважды: сначала с некоторым шагом h (число шагов n) – S1N, а затем с шагом h/2 (число шагов 2n) – S2N.
Если
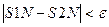 , (9)
, (9)
где 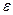 – допустимая погрешность, то полагать
– допустимая погрешность, то полагать
S=S2N.
Если же окажется, что 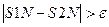 , то расчет повторить с шагом h/4 и так до тех пор, пока не выполнится условие (9).
, то расчет повторить с шагом h/4 и так до тех пор, пока не выполнится условие (9).
Погрешность вычисления
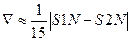 . (10)
. (10)
В случае выполнения условия (9) обязательно
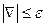 (11)
(11)
В качестве начального значения шага можно выбрать число
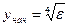 (12)
(12)
|
|
|


