 |
Модели в пространстве состояний
|
|
|
|
ЛЕКЦИЯ 3 МОДЕЛИ ЛИНЕЙНЫХ ОБЪЕКТОВ
Дифференциальные уравнения
Составляя модель объекта на основании физических законов, мы чаще всего получаем систему дифференциальных уравнений первого и второго порядка.
Для примера покажем, как построить модель двигателя постоянного тока, используя законы механики и электротехники. Вход этого объекта – напряжение якоря u (t) (в вольтах), выход – угол поворота вала θ (t) (в радианах).
Сначала вспомним некоторые «житейские» знания об электродвигателях. Вал двигателя начинает вращаться, когда приложено напряжение питания. Если напряжение не меняется, угловая скорость вращения ω(t) (в радианах в секунду) остается постоянной, при этом угол θ (t) равномерно увеличивается.
Чем больше напряжение, тем быстрее вращается вал. Если зажать вал рукой (или подключить нагрузку, например, заставить двигатель вращать турбину), скорость вращения постепенно уменьшается до нового значения, при котором вращающий момент двигателя будет равен моменту сопротивления (нагрузки). Пока эти моменты равны, скорость вращения остается постоянной и ее производная равна нулю.
Рисунок 3.1 – Вращение вала ДПТ
Теперь переведем эти рассуждения на строгий язык математики. Угловая скорость вращения ω(t) вычисляется как производная от угла поворота вала θ (t), то есть 
. Соответственно, угол θ (t) – это интеграл от угловой скорости. В механике уравнение вращательного движения обычно записывают в виде
,
где M (t) – вращающий момент (измеряется в H·м), MH (t) – момент нагрузки (возмущение, также в H·м). Буквой J обозначен суммарный момент инерции якоря и нагрузки (в кг·м2). Величина момента инерции говорит о том, насколько легко «разогнать» двигатель (чем больше момент инерции, тем сложнее «разогнать»).
|
|
|
Перейдем к электротехнике. В нашем случае момент M (t) – это электромагнитный момент двигателя, который вычисляется по формуле
,
где CМ – коэффициент, Φ – магнитный поток, создаваемый обмоткой возбуждения (измеряется в веберах); i (t) – ток якоря (в амперах), который может быть найден из уравнения
,
где e (t) – электродвижущая сила (ЭДС) якоря (в вольтах) и R – сопротивление якорной цепи (в омах). В свою очередь, ЭДС рассчитывается через магнитный поток и частоту вращения
,
где Cω – коэффициент. Вводя новые постоянные 
и 
, можно записать модель двигателя в виде системы уравнений
, 
, , . (1)
Модель (1) описывает связи реальных сигналов в системе, ее внутреннее устройство.
Часто нам достаточно знать, как будет реагировать объект на заданный входной сигнал (управление). При этом его внутреннее устройство нас не очень интересует, то есть мы рассматриваем объект в качестве «черного ящика». Подставив второе уравнение из системы (1) в четвертое, найдем i (t) и подставим в первое уравнение. Переходя к переменной θ (t), получаем
,
или, перенося все члены, зависящие от θ (t), в левую часть равенства
. (2)
Это дифференциальное уравнение второго порядка, связывающее вход u (t) и нагрузку MH (t) с выходом θ (t). В сравнении с системой (1), все внутренние сигналы исходной модели (e (t) и i (t)) были исключены из уравнений. Поэтому уравнение (2) называется уравнением «вход-выход».
Порядком модели называют порядок соответствующего дифференциального уравнения. В данном случае мы получили модель второго порядка.
В этом разделе на простом примере мы посмотрели, как на основе физических законов строятся математические модели объектов управления. Как правило, они представляют собой дифференциальные уравнения.
Модели в пространстве состояний
|
|
|
Для того, чтобы было легче исследовать модель объекта, желательно привести ее к некоторому стандартному виду, для которого уже есть готовые общие решения. Таким «стандартом» в теории управления считается система дифференциальных уравнений первого порядка, которая называется нормальной формой Коши.
Рассмотрим снова модель электродвигателя, считая, что MH (t)=0 (нагрузки нет). Вспомнив, что 
, можно записать (2) в виде системы
.
Эта система дифференциальных уравнений первого порядка быть записана в матричной форме
. (3)
Значения θ (t) и ω (t) определяют состояние двигателя в момент времени t. Это значит, что зная их значения в некоторый момент времени t0 и входной сигнал u (t) при всех t ≥ t0 можно рассчитать поведение объекта для любого последующего момента. При этом предыдущие значения θ (t), ω (t) и u (t) (при t < t 0) не играют никакой роли. Поэтому θ (t) и ω (t) называются переменными состояния, а вектор 
- вектором состояния.
В теории управления принято обозначать вектор состояния через x (t), вход объекта (сигнал управления) – через u (t). Тогда модель (3) может быть записана в виде
, (4)
где 
, 
, 
. Модель (4) связывает вход u (t) и вектор состояния x (t), поэтому она называется моделью вход-состояние.
Полная модель объекта в пространстве состояний содержит еще одно уравнение – уравнение выхода, которое показывает, как формируется выход объекта y (t)
, (5)
Эта модель называется моделью вход-состояние-выход. Выходная координата для двигателя постоянного тока – это угол поворота вала
,
так что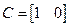 
и D =0. Если же в качестве выхода принять угловую скорость, то 
.
С помощью модели (5), изменяя матрицы C и D, можно принять за выход любую линейную комбинацию переменных состояния и входа. Во многих практических задачах выход – это одна или несколько переменных состояния, которые мы можем измерить.
Поскольку момент инерции J, сопротивление якоря R и коэффициенты k1 и k2 не зависят от времени, матрицы A, B, C и D в модели (5) – постоянные. Такие объекты называются стационарными, в отличие от нестационарных объектов, параметры которых изменяются во времени.
Запись моделей в единой форме (5) позволяет отвлечься от смысла переменных состояния и исследовать системы разной природы стандартными методами, которые хорошо разработаны и реализованы в современных компьютерных программах.
|
|
|
Пример, как уравнения вида (5) могут быть решены и чем удобна именно такая форма записи. Предположим, что известны начальные условия, то есть вектор состояния x (0) при t = 0. Знание x (0) и входа u (t) при всех t > 0 дает возможность однозначно определить дальнейшее поведение этого объекта.
Первое уравнение в (5) позволяет найти производную, то есть, скорость изменения вектора состояния x (t) в любой момент времени. Будем считать, что при 0 ≤ t ≤ Δ t, где Δ t – малый интервал времени, эта производная не меняется. Тогда значение вектора состояния при t = Δ t приближенно определяется формулой
,
то есть, его можно легко вычислить. Зная x (Δ t) и сигнал управления u (Δ t), находим выход системы в тот же момент
.
Таким образом, можно (приближенно) рассчитать выход системы при всех t > 0. Конечно, точность будет тем выше, чем меньше Δ t, однако объем вычислений при этом также увеличится. Этот метод приближенного решения дифференциальных уравнения называется методом Эйлера. Так как не делается никаких предположений о постоянных матрицах A, B, C и D, его (как и другие, более совершенные методы) можно использовать без изменений для решения любых уравнений вида (5).
Переходная функция
Один из методов построения моделей «вход-выход» – определение реакции объекта на некоторый стандартный сигнал. Один из простейших сигналов – так называемый «единичный скачок» («единичный ступенчатый сигнал»), то есть мгновенное изменение входного сигнала с 0 до 1 в момент t = 0. Формально этот сигнал определяется так
.
Реакция объекта на единичный скачок называется переходной функцией и обозначается h (t)
Рисунок 3.2 – График переходной функции h(t)
При этом предполагается, что объект в начальный момент находится в состоянии покоя, то есть, имеет нулевые начальные условия. Это значит, что все его переменные состояния равны нулю и внутренняя энергия также нулевая.
Если начальные условия ненулевые, то для построения сигнала выхода при любом входе нужно использовать дифференциальные уравнения объекта или модель в пространстве состояний. Это значит, что переходная характеристика дает меньше информации, чем исходные уравнения.
|
|
|
Пусть модель объекта задана дифференциальным уравнением первого порядка
, (6)
где k – безразмерный коэффициент, а T – некоторая постоянная, которая имеет размерность времени (измеряется в секундах). Найдем переходную характеристику этого звена. Решая уравнение (6) при x (t) = 1 (t > 0), получаем
,
где постоянная C1 должна определяться из начальных условий. Поскольку нас интересует переходная характеристика, начальные условия считаем нулевыми, то есть y (0) = 0, что дает C1 = − k и поэтому
. (7)
На рисунке показаны переходные характеристики (7) при различных значениях параметра T, который называется постоянной времени звена
Рисунок 3.3 – Переходные характеристики
Видно, что при увеличении T выход y медленнее достигает установившегося значения, равного k, то есть постоянная времени характеризует инерционность звена (6). Чем больше постоянная времени, чем медленнее реагирует объект на управление и тем больше усилий нужно для того, чтобы перевести его в новое состояние.
Заметим, что ступенчатый сигнал легко получить на практике, поэтому переходную характеристику можно снять экспериментально.
|
|
|
