 |
Импульсная характеристика (весовая функция)
|
|
|
|
В качестве тестового сигнала можно, в принципе, использовать любой сигнал. Например, можно изучать реакцию системы на прямоугольный импульс. Вопрос в том, чтобы определить некоторый стандартный вид этого импульса. На рисунках а)-в) показаны три импульса, имеющих одинаковые площади. Для простоты будем считать, что эта площадь равна единице.
Рисунок 3.4 – Импульсная функция
Что будет, если мы будем уменьшать ширину импульса, сохраняя его площадь? Очевидно, что высота импульса будет расти и в пределе (когда ширина стремится к нулю) станет бесконечной. Таким образом, мы получили еще один классический тестовый сигнал – единичный импульс или дельта-функцию Дирака δ (t). Это идеальный (невозможный в реальной жизни) сигнал, который равен нулю во всех точках, кроме t =0, где он уходит к бесконечность, причем его площадь (интеграл по всей оси времени) равен единице
.
Поскольку бесконечный импульс невозможно нарисовать, на графике он изображается стрелкой, высота которой равна единице (см. рисунок г).
Иногда определяют дельта-функцию как производную от единичного ступенчатого сигнала 1 (t). Действительно, эта производная равна нулю при всех значениях t, кроме нуля, где она обращается в бесконечность.
Реакция системы на единичный импульс (дельта-функцию) называется импульсной характеристикой и обозначается w (t)
Рисунок 3.5 – График импульсной функции
Импульсная характеристика, так же, как и переходная характеристика, определяется при нулевых начальных условиях, то есть, объект должен находиться в состоянии покоя.
Рассматривая дельта-функцию как предельный случай прямоугольного сигнала единичной площади, можно найти связь между переходной функцией и импульсной характеристикой.
|
|
|
Пусть ширина прямоугольного импульса равна ε, а высота – 1/ ε. Такой импульс можно представить в виде разности двух ступенчатых сигналов
,
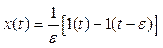где 1 (t − ε) – это единичный ступенчатый сигнал, который приходит в момент t = ε, то есть, смещен по времени на ε (см. рисунок далее).
Так как для линейных систем справедлив принцип суперпозиции, сигнал на выходе будет равен разности реакций системы на входы 1 (t) и 1 (t −ε), умноженной на коэффициент 1/ε. Учитывая, что реакция на сигнал 1 (t) – это переходная функция h (t), получаем
.
Переходя к пределу при ε →0, находим, что импульсная характеристика
,
как оказывается, равна производной от переходной функции. Наоборот, переходная функция – это интеграл от импульсной характеристики на интервале от 0 до t
.
Дифференцируя переходную характеристику (7) звена первого порядка, получаем соответствующую импульсную характеристику
.
Другое название импульсной характеристики – весовая функция. Это название связано с тем, что для произвольного входного сигнала x (t) выход системы y (t) при нулевых начальных условиях вычисляется как интеграл
.
Здесь функция w (t) как бы «взвешивает» входной сигнал x (t) в подынтегральном выражении. Импульсная характеристика дает неполную информацию об объекте, поскольку не учитывает ненулевые начальные условия.
В отличие от ступенчатого сигнала, мгновенный импульс бесконечной величины невозможно получить на реальном устройстве, поэтому снять импульсную характеристику системы, строго говоря, экспериментально не удается.
Передаточная функция
Выходной сигнал системы можно представить как результат действия некоторого оператора на ее вход. Для линейных моделей такой оператор можно записать следующим образом.
Пусть модель объекта задана линейным дифференциальным уравнением второго порядка, связывающим вход x (t) и выход y (t)
|
|
|
, (8)
где ai (i = 0,1) и bi (i = 0,1,2)– постоянные.
Введем оператор дифференцирования 
, который действует на сигнал x (t) по правилу 
.
Теперь запишем производные сигналов x (t) и y (t) по времени в операторной форме
.
Подставляя эти выражения в (8), получим
. (9)
Можно формально вынести за скобки y (t) в левой части равенства (9) и x (t) в правой части
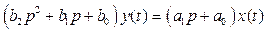. (10)
Левая часть (10) означает, что оператор 
действует на сигнал y (t), а в правой части оператор 
действует на сигнал x (t). «Разделив» (условно, конечно) обе части (10) на оператор , связь выхода и входа можно записать в виде
, (11)
где запись W (p)· x (t) означает не умножение, а действие сложного оператора
(12)
на сигнал x (t). Иначе говоря, формула y (t)= W (p)· x (t) – это не что иное, как символическая запись уравнения (8), которую удобно использовать.
Функция W (p) называется передаточной функцией объекта, который описывается уравнением (8). Она полностью описывает связи между выходом и входом объекта при нулевых начальных условиях, но не учитывает его внутреннее устройство.
Часто передаточной функцией называют функцию W (λ), которая получается из (12) в результате замены оператора p на некоторую независимую переменную λ. Эта фукнция представляет собой отношение двух полиномов (многочленов) от λ.
Передаточная функция W (λ) называется правильной, если степень ее числителя не больше, чем степень знаменателя; строго правильной, если степень числителя меньше степени знаменателя; неправильной, если степень числителя больше, чем степень знаменателя. Например, функция 
– строго правильная и одновременно правильная; 
– правильная, но не строго правильная (иногда такие функции называют биправильными), а 
– неправильная.
Нулями передаточной функции называются корни ее числителя, а полюсами – корни знаменателя. Например, функция 
имеет нуль в точке λ = 1 и два полюса в точках λ = −1 и λ = −2.
|
|
|
