Главная | Обратная связь | Поможем написать вашу работу!
 МегаЛекции

Вывести все совершенные числа в данном диапазоне.




program sov2proc; { Задача. Вывести все совершенные числа в данном диапазоне.} var a, b, m: longint; procedure sov(c, d: longint; var l: longint);var j, i, s: longint;begin for i:= a to b do begin s:= 0; for j:= 1 to i - 1 do if i mod j = 0 then s:= s + j; if s = i then writeln(i); end;end; begin write('Введите диапазон для вывода совершенных чисел: '); readln(a, b); writeln('Совершенные числа в данном диапазоне:'); sov(a, b, m); readln;end. 3.Введенное число - полиндром? program poly_3func; { Задача. Введенное число - полиндром?} var chislo: longint; function poly(n: longint): boolean;var a, b: longint;begin a:= n; b:= 0; while a <> 0 do begin b:= b * 10 + a mod 10; a:= a div 10; end; if n = b then poly:= true else poly:= false;end; begin write('Введите число: '); readln(chislo); case poly(chislo) of true: writeln('Ваше число - полиндром.'); false: writeln('Ваше число - не полиндром.'); end; readln;end. 4. Вывести заданное количество членов функции: 1+1!/2**1+2!/2**2+...+n!/2**n program summ_rada_func; { Задача. Вывести заданное количество членов функции: 1+1!/2**1+2!/2**2+...+n!/2**n} var m: integer; function fac(n: integer): longint;var i, rez: longint;begin rez:= 1; for i:= 2 to n do rez:= rez * i; fac:= rez;end; function st(n: integer): longint;var i, r: longint;begin r:= 2; for i:= 1 to n do r:= r * 2; st:= r;end; function summ_rada(n: integer): real;var s: real; i, j: integer;begin s:= 1; for i:= 1 to n do s:= s + (fac(i) / st(i)); summ_rada:= s;end; begin write('Количество членов равно '); readln(m); writeln('Сумма членов равна ', summ_rada(m):0:4); readln;end.
  : Понятие рекурсии  
   

Рекурсия (от латинского recursio - возвращение) - это такой способ организации вычислительного процесса, при котором процедура или функция в ходе выполнения составляющих ее операторов обращается сама к себе.

Для того, чтобы такое обращение не было бесконечным, в тексте подпрограммы должно быть условие, по достижению которого дальнейшего обращения не происходит. таким образом, рекурсивное обращение может включаться только в одну из ветвей подпрограммы.

В языке Паскаль нет никаких ограничений на рекурсивные вызовы подпрограмм, необходимо только понимать, что каждый очередной рекурсивный вызов приводит к образованию новой копии локальных объектов подпрограммы и все эти копии, соответствующие цепочке активизированных и не завершенных рекурсивных вызовов, существуют независимо друг от друга

Рекурсия достаточно широко применяется в программировании, что основано на рекурсивной природе многих математических алгоритмов. А также Вы должны знать, что любой рекурсивный алгоритм можно преобразовать в эквивалентный итеративный (то есть использующий циклические конструкции).

В больших и сложных программах иногда приходится заменять рекурсию на итерацию. Дело в том, что рекурсия связана с многократными вызовами процедур, а это несколько менее эффективно при выполнении по сравнению с использованием циклов. Однако рекурсивные версии программ, как правило, гораздо короче и нагляднее.

Хорошей иллюстрацией механизма рекурсии является функция для вычисления факториала натурального числа. Вспомним, что факториалом числа называется произведение всех натуральных чисел от 1 до этого числа включительно:

N! = 1*2*3*... *(N-2)*(N-1)*N
1! = 1
0! = 1

Сначала покажем обычную не рекурсивную функцию для вычисления факториала, которая реализует итеративный алгоритм вычисления:

Function NonRecFact(N:integer): LongInt;
Var
i: integer; {переменная цикла }
Res: LongInt; {результат}
Begin
Res:= 1;
for i:= 1 to N do
res:= Res*i;
NonResFact:= Res;

End;

Вторая функция использует рекурсивные обращения, что делает ее гораздо компактнее, и основана на очевидном соотношении:

N! = (N-1)!*N

Иными словами, чтобы получить значение факториала от числа N, достаточно умножить на N значение факториала от предыдущего числа:

Function RecFact(N:integer): LongInt;
Begin
if N <= 1
then
ResFact:= 1
else
ResFact:= N*ResFact(N-1);
End;

Полностью программа, вычисляющая факториал числа, будет выглядеть так:

Program Rekurs;
Var
N: integer;
F: Longint;
{ - - - - - - - - - - - - - - - - - - - -}
Function RecFact(N:integer): LongInt;
Begin
if N <= 1
then
ResFact:= 1
else
ResFact:= N*ResFact(N-1);
End;
{ - - - - - - - - - - - - - - - - - - - -}
Begin
writeln('Введите число N > ';
read(N);
F:= RecFact(N);
writeln('Для числа ',N,' значение факториала равно ',F);
End.

После запуска программы на экран выводится запрос "Введите число N > ", затем с клавиатуры считывается введенное значение и в выражении F:=RecFact(N) вызывается функция RecFact с параметром-значением N. В подпрограмме-функции проверяется условие N<=1. Если оно выполняется, то функции ResFact присваивается значение 1 и на этом выполнение подпрограммы завершается. Если условие N<=1 не соблюдается, то выполняется вычисление произведения N*ResFact(N-1). Вычисление произведения носит рекурсивный характер, так как при этом осуществляется вызов функции ResFact(N-1), значение которой вычисляется, в свою очередь, через вызов функции ResFact, параметром которой также будет функция ResFact, и т.д., до тех пор пока значение формального параметра N не будет равно 1. Так как базовая часть описания рекурсивной функции ResFact определяет значение ResFact для N=1, равным единице, то рекурсивные вызовы функции ResFact больше не выполняются, а наоборот выполняется вычисление функции ResFact для чисел, возрастающих от 1 до N, причем функция ResFact всякий раз возвращает значение, равное произведению очередного числа на факториал от предыдущего числа. Последнее возвращение результата вычисления функции ResFact присвоит переменной F значение произведения всех чисел от 1 до N, т.е. факториал числа N.

Итак, при выполнении рекурсивной подпрограммы осуществляется многократный переход от некоторого текущего уровня организации алгоритма к нижнему уровню последовательно до тех пор, пока не будет получено тривиальное решение поставленной задачи. В нашем примере решение при N=1 тривиально, т.е. ResFact=1. Затем осуществляется возврат на верхний уровень с последовательным вычислением значения функции ResFact.

Задание. Введите текст рассмотренной выше программы и запишите файл на диск под соответствующим именем, а затем откомпилируйте его. После того, как компиляция закончится успешно, задайте для просмотра в окне отладчика переменные N, F. Установите видимыми одновременно окна редактора с текстом программы и окно просмотра. Исполните программу в пошаговом режиме с заходом в функцию и пронаблюдайте за изменением значения переменной N при рекурсивных вызовах функции ResFact.

Задание. Напишите программы, демонстрирующие выполнение рекурсивного и итеративного алгоритма для задач:

  1. На печать выводится сказка “О попе и его собаке” определенное число раз. ("У попа была собака, он ее любил. Она съела кусок мяса - он ее убил. В землю закопал, надпись написал...)
  2. Напишите рекурсивный алгоритм нахождения степени числа. ах=ах-1*а, а0=1
  Примеры задач рекурсивного решения в текстовом и графическом режимах  
   

Задача 1. Нахождение n-го члена арифметической прогрессии

(an=a1+d*(n-1)-формула n-го члена арифметической прогрессии).

Program Progressiy;
Var
a1, d, k: real;
n: integer;
{ - - - - - - - - - - - - - - - - - - - -}
Function Arif (a1, d: real; n: integer): real;
Begin
if n = 1
then
Arif:= a1
else
Arif:= Arif(a1, d, n - 1) + d;
End;
{ - - - - - - - - - - - - - - - - - - - -}
Begin
writeln('Задайте первый член прогрессии');
readln(a1);
writeln('Задайте разность арифметической прогрессии');
readln(d);
writeln('Арифметическая прогрессия ', Аrif(a1, d, n): 4: 2);
End.

Задание. Составьте программу

a) нахождения n-го члена геометрической прогрессии,
б) нахождения суммы членов арифметической прогрессии,
в) нахождения суммы членов геометрической прогрессии,
г) нахождения n-го члена ряда Фибоначчи.

Задача 2. Вложенность квадратов.

Program KaparovS;
Uses
Crt, Graph;
Var
x, y, x1, y1, x2, y2, x3, y3, n, d, a, b: integer
{ - - - - - - - - - - - - - - - - - - - -}
Procedure Pic(x, y, x1, y1, x2, y2, x3, y3, n, d: integer);
Var
k, j: integer;
Begin
if n >=1
then
begin
Line(x, y, x1, y1);
Line(x1, y1, x2, y2);
Line(x2, y2, x3, y3);
Line(x3, y3, x, y);
j:= x;
k:= y;
x:= (x1-x) div 2 + x;
y:= (y1-y) div 2 + y;
x1:= (x2-x1) div 2 + x1;
y1:= (y2-y1) div 2 + y1;
x2:= (x3-x2) div 2 + x2;
y2:= (y3-y2) div 2 + y2;
x3:= (j-x3) div 2 + x3;
y3:= (k-y3) div 2 + y3;
Pic(x, y, x1, y1, x2, y2, x3, y3, n-1, d);
end;
End;
{ - - - - - - - - - - - - - - - - - - - -}
Begin
ClrScr;
write ('Введите количество повторений: ');
readln (n);
x:= 0;
y:= 0;
x1:= 400;
y1:= 0;
x2:= 400;
y2:= 400;
x3:= 0;
y3:= 400;
a: Detect;
InitGraph(a, b, 'D:\TP7\BGI');
ClearDevice;
Setcolor(Green);
Pic(x, y, x1, y1, x2, y2, x3, y3, n, d);
readln;
CloseGraph;
End.

Задание. Наберите программу и просмотрите ее действие. Дополните программу комментарием. По желанию улучшите алгоритм.

Творческое задание. Придумайте и решите задачу на демонстрацию рекурсии в графическом режиме.

 

  Косвенная рекурсия.  
   

Рассмотренные выше программы использовали так называемую прямую рекурсию, когда в теле некоторой процедуры содержался непосредственный вызов самой себя. В языке Паскаль допускается также и косвенная рекурсия, когда, например, процедура, процедура А вызывает процедуру В, а та, в свою очередь,- процедуру А. Длина таких цепочек вызовов может быть произвольной, однако при разработке программы необходимо тщательно следить за тем, чтобы рекурсивный алгоритм был сходимым, то есть не приводил к бесконечным взаимным вызовам подпрограмм.

Образно косвенную рекурсию можно описать так. Перед зеркалом 1 стоит зеркало 2, в котором отражается само зеркало 1. В последнем видно зеркало 2 и т.д.

Приведем пример программы, иллюстрирующей косвенные рекурсивные вызовы процедур. В этой программе процедуры Rec1 и Rec2 рекурсивно вызывают друг друга, поочередно уменьшая свои фактические параметры. Легко видеть, что обе процедуры работают с одной глобальной переменной А, которая передается в них по ссылке. Критерием завершения работы является обращение этой переменной в ноль.

Обратите внимание, что в программе необходимо предварительное определение второй процедуры Rec2, так как ее вызов встречается в процедуре Rec1, т.е. перед ее полным описанием.

Program KosvRecurs;
Var
A: integer;
Procedure Rec2 (Var Y:integer); Forward;
{ - - - - - - - - - - - - - - - - - - - -}
Procedure Rec1 (Var X:integer);
Begin
X:= X-1;
if X>0
then
Rec2;
writeln (X)
End;
{ - - - - - - - - - - - - - - - - - - - -}
Procedure Rec2 (Var Y:integer);
Begin
Y:= Y div 2;
if Y>2
then
Rec1;
writeln (Y)
End;
{ - - - - - - - - - - - - - - - - - - - -}
Begin
A:= 15;
Rec1(A);
End.

Творческое задание. Придумайте и решите задачу на демонстрацию косвенной рекурсии в графическом режиме.

 

 

  Решение задач.  
   
  1. Определите члены последовательность Фибоначчи.
  2. Найдите максимальный элемент в одномерном массиве.
  3. Составьте алгоритм вычисления суммы
    .
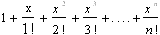    Указание. Обозначьте и используйте соотношения
  4. Вычислите
  5. Определите n-й член последовательности, в которой каждый следующий член равен сумме обратных величин всех предыдущих.
  6. Определите n-й член последовательности, в которой каждый следующий член равен сумме квадратов всех предыдущих.
  7. При положительном а решением уравнения х=х/2+а/(2х) служит х=√a. Рекуррентное соотношение
    можно использовать для быстрого вычисления √a. Определите корень квадратный числа а.
  8. Составьте алгоритм для вычисления 3√a, используя соотношение
  9. Составьте алгоритм, вычисляющий n-й член последовательности, заданной соотношениями:
  10. Составить рекурсивную программу ввода с клавиатуры последовательности чисел (окончание ввода - 0) и вывода ее на экран в обратном порядке.

Для сдачи зачета приготовьте файлы и листинги с решенными задачами, а также будьте готовы ответить на теоретические вопросы, рассмотренные в этой теме.

Для любознательных
Поделиться:





Воспользуйтесь поиском по сайту:



©2015 - 2024 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...