 |
§ 35. Обращение простых интервалов
|
|
|
|
м. 6 ув. 5
§ 35. Обращение простых интервалов
Обращением интервала называется результат перемены мест составляющих его тонов, когда основание становится вершиной, а вершина — основанием интервала.
При обращении обязательно образуется новый интервал, который вместе с первоначальным непременно составляет октаву. Однако числовое выражение суммы обоих интервалов (данного и его обращения) всегда будет равняться 9 (а не 8), так как во взаимообратимых интервалах один из звуков считается дважды, ибо входит как в первый, так и во второй интервал. Итак:
| прима | обращается в | октаву | (1 + 8 = 9) | квинта | — »— | кварту | (5 + 4 = 9) | |
| секунда | — »— | септиму | (2 + 7 = 9) | секста | — »— | терцию | (6 + 3 = 9) | |
| терция | — »— | сексту | (3 + 6 = 9) | септима | — »— | секунду | (7 + 2 = 9) | |
| кварта | — »— | квинту | (4 + 5 = 9) | октава | — »— | приму | (8 + 1 = 9) |
Из приведенной таблицы видно, что тесные интервалы (от примы до кварты включительно) обращаются в широкие (от квинты до октавы включительно) и наоборот.
Сам процесс обращения простых интервалов сводится к следующему: один из звуков данного интервала переносится на октаву в сторону, противоположную его местонахождению (основание — вверх или вершина — вниз), а другой звук при этом остается на месте, в результате чего образуется новый интервал, являющийся обращением первого, где функции составляющих его звуков меняются ролями: основание становится вершиной, а вершина — основанием. Если подвергающийся переносу на октаву звук был альтерированным, то он сохраняет свой знак альтерации:
|
|
|
79 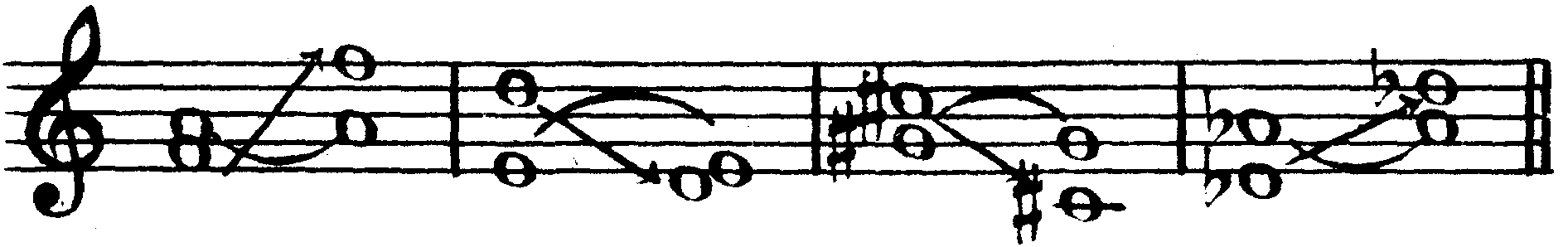
Что же касается вида интервала, определяемого, как известно, его тоновой величиной, то при обращении все интервалы (за исключением чистых) получают противоположный вид, то есть большие интервалы обращаются в малые, увеличенные — в уменьшенные, дважды увеличенные — в дважды уменьшенные и наоборот. Только чистые интервалы при обращении сохраняют свой вид и обращаются тоже в чистые интервалы. Сумма тонов обоих взаимообращающихся интервалов всегда равняется 6 тонам (то есть тоновой величине чистой октавы):
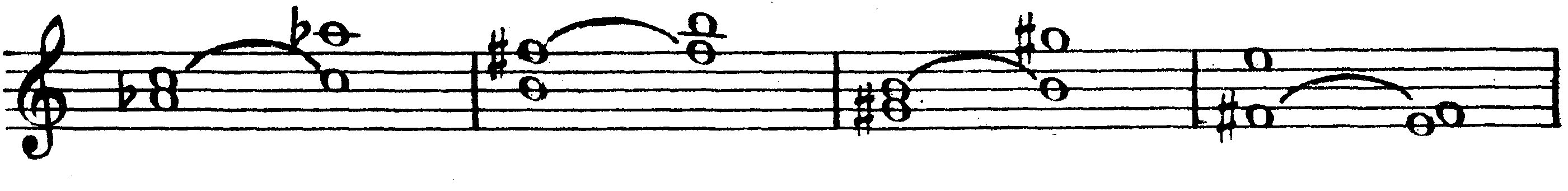
б. 3 м. 6 ч. 5 ч. 4 м. 3 б. 6 м. 7 б. 2
2 т. + 4 т. 3 1/2 т. +2 1/2 т. 1 1/2 + 4 1/2 + 5 т. + 1 т.

ум. 4 ув. 5 дв. ув. 4 дв. ум. 5 ч. 1 ч. 8 ув. 6 ум. 3
2 т. + 4 т. 3 1/2 т. + 2 1/2 т. 0 т. + 6 т. 5 т. + 1 т.
Другие же категории, характеризующие те или иные интервалы, при обращении последних не изменяются. Так, диатонические интервалы обращаются тоже в диатонические, при обращении хроматических снова образуются хроматические интервалы. Консонансы обращаются в консонансы, а диссонансы — в диссонансы. При обращении простых интервалов, как правило, образуются тоже простые интервалы.
§ 36. Обращение составных интервалов
Обращение составных интервалов может производиться одним из следующих двух способов:
1) один из звуков составного интервала переносится на две октавы в сторону, противоположную его местонахождению (основание — вверх или вершина — вниз), а другой звук при этом остается на месте;
2) оба звука составного интервала одновременно переносятся на одну октаву навстречу друг другу, перекрещиваясь при этом.
В обоих случаях образуется простой интервал, являющийся обращением данного составного интервала. Второй способ часто оказывается более предпочтительным, так как позволяет избегать появления многих добавочных линий у отдельных нот и делает саму запись более компактной и удобочитаемой.
|
|
|
В остальном следует руководствоваться сказанным выше в отношении обращения простых интервалов. Однако надо иметь в виду, что в творческой композиторской практике проблема обращения интервалов понимается и осуществляется несравненно шире и свободнее, чем в учебном курсе теории музыки. Так, например, в полифонических пьесах, где нередко встречается так называемый двойной вертикально-подвижной контрапункт* [Двойным вертикально-подвижным контрапунктом называется полифонический прием, при котором голоса меняются местами по вертикали: нижний становится верхним и наоборот. ] можно увидеть, что простые интервалы обращаются в составные (и даже в ультраширокие), составные — в ультраширокие (или тоже составные), ультраширокие — в простые и т. д. Обязательным условием при обращении любых интервалов является перекрещивание голосов, перемена их местами, иначе не образуется нового интервала, являющегося обращением первого. Ниже приводится пример обращения составных интервалов обоими описанными способами:
81 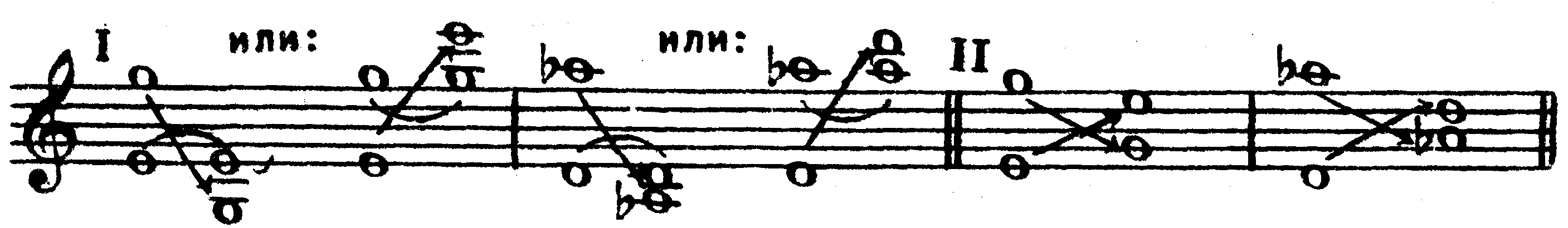
м. 10 б. 6 м. 10 б. 6 ум. 12 ув. 4 ум. 12 ув. 4 ум. 10 б. 6 ум. 12 ув. 4
|
|
|


