 |
3.2.2 Исследования гидродинамики в системе жидкость-жидкость
|
|
|
|
3. 2. 2 Исследования гидродинамики в системе жидкость-жидкость
Опыты проводились на установке, изображенной на рисунке 9. Внимание обращалось на поведение масло-спиртовой смеси в прозрачной трубке 5 с внутренними диаметрами 2 мм и 5 мм и длиной 230 мм (см. рисунок 15).
Рисунок 15 - Трубка
Последовательность действий при выполнении опытов (см. рисунок 12) была следующей:
1. Наполняем соответствующие емкости 1 и 2 маслом и спиртом.
2. Устанавливаем рабочие расходы на насосах 3.
3. Одновременно включаем насосы.
4. С помощью фотоаппарата ведем фотосъемку наблюдаемого режима.
5. По окончании всех опытов промываем установку чистой водой и просушиваем воздухом.
По методике, описанной выше, проведена серия опытов с различными расходами масла и спирта.
Таблица 6 – Расходы масла и спирта при проведении опытов
| Qмасла, мл/мин | Qспирта, мл/мин |
| 10, 4 | 5, 3 |
| 15, 1 | 5, 3 |
| 20, 8 | 5, 3 |
| 25, 5 | 5, 3 |
| 30, 2 | 5, 3 |
| 50, 1 | 5, 3 |
| 5, 3 | |
| 64, 3 | 6, 4 |
Фотографии с режимами течения не поддались обработке. Но визуально оптимальные расходы компонентов составляют Qмасла=53 мл/мин; Qспирта=5, 3 мл/мин. При таких расходах наблюдался более равномерный снарядный режим (см. рисунок 11) по сравнению с другими расходами.
3. 2. 3 Скорость уноса частиц
Для начала определим скорость потока масла в трубке, при котором начинается движение частиц с ферментом. Итак, для определения скорости начала ожижения воспользуемся формулой Тодеса[8, 9]
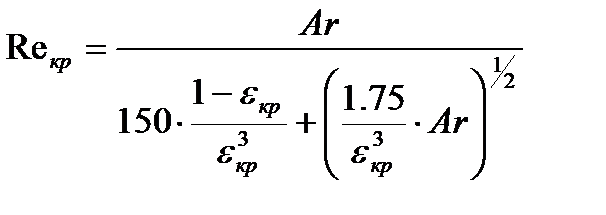, (4)
При беспорядочной загрузке порозность неподвижного слоя составляет 
, при подстановке 
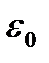в формулу Тодеса получим
|
|
|
(5)
Находим значение критерия Архимеда
, (6)
(7)
где 
- средний размер частиц с ферментом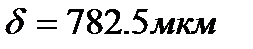 
- плотность частиц 
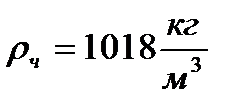
, (8)
Верхний предел существования кипящего слоя часто связывают с понятием скорости витания частиц, при котором начинается массовый унос частиц. Начало уноса частиц из слоя происходит при скорости масла, равной скорости витания частиц. Верхний предел существования кипящего слоя часто связывают с понятием скорости витания частиц, при которой начинается массовый унос частиц. [9]
Для расчета скорости уноса частиц существуют ряд формул, но существует универсальная формула Тодеса, приближенно пригодная для всех режимов[8].
, (9)
Скорость 
, (10)
Рабочая скорость 
лежит в пределах
3. 2. 4 Расчет скорости движения частиц в трубке
Для начала определим скорости в каждой точке трубки, изображенной на рисунке 16. Для этого разобьем участок на равные отрезки (рисунок 17) и отложим график зависимости диаметра от длины (рис. 18). Далее строим график площади сечения от длины (рис. 19), а затем, зная расход смеси (Qсм=Qмасла+Qспирта=53+ 5, 3= 58, 3мл/мин), построим зависимость скорости от длины (рис. 20).
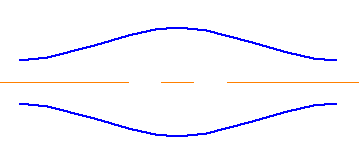
Рисунок 16 - Участок трубки
Рисунок 17 - Разбиение на равные участки
Рисунок 18 - График зависимости диаметра от длины
Рисунок 19 - График зависимости площади сечения от длины
Рисунок 20 - График зависимости скорости от длины
Запишем уравнение движения частицы
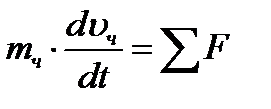, (11)
где 
- сумма всех сил, действующих на частицу; 
- масса частицы.
|
|
|
z
Рисунок 21 - Силы, действующие на частицу при осаждении
Подставляя 
и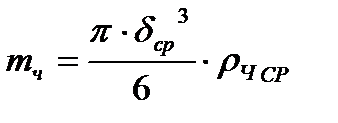 
в уравнение (11), получим
, (12)
где 
- вязкость смеси (0, 043 Па*с);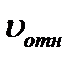 
- скорость относительного движения 
; 
= 
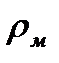- плотность масла
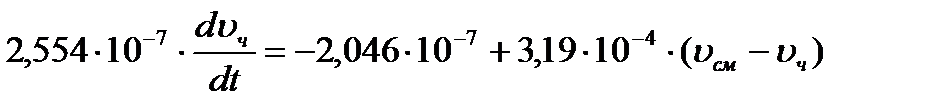
Уравнение (12) решается численным интегрированием, т. е.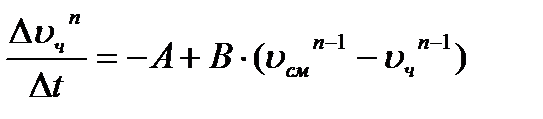 
; 
при 
.
Начальное условие: 
; 
; 
; 
.
Программа, реализующая решение численного интегрирования:
Строим график зависимости 
от длины участка на графике 
(рис. 20) 
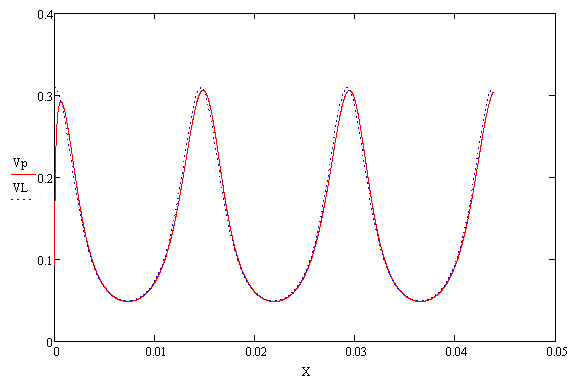
Рисунок 22 – График скоросте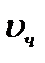й 
и 
Из графика (рис. 22) видно, что существует относительная скорость частиц, которая описывалась в п. 3. 1. 2. Малое смещение графиков говорит о том, что плотность частиц близка к плотности жидкости.
Запишем уравнение Бернулли для произвольных сечений канала:
(13)
(14)
(15)
Подставляя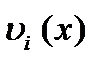 
и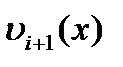 
, найдем распределение давления по участку канала (рис. 20).
Рисунок 23 - Распределение давления
|
|
|
