 |
Способы нормирования и формы выражения характеристик
|
|
|
|
Погрешности
Для большинства СИ, используемых в статическом режиме, нормируют пределы допускаемых погрешностей по ГОСТ 8.401-80 «Классы точности средств измерений. Общие требования».
Согласно этому стандарту пределы допускаемых основной и дополнительных погрешностей выражают в форме приведенных, относительных или абсолютных погрешностей в зависимости от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения СИ.
Нормирование пределов абсолютной основной погрешности применяется, если погрешность таких измерений принято выражать в единицах измеряемой величины или в делениях шкалы. Например, пределы допускаемых погрешностей мер массы или длины.
В остальных случаях используют нормирование пределов приведенной или относительной основной погрешности. Выражение пределов допускаемой погрешности в форме приведенных и относительных погрешностей является предпочтительным, так как они позволяют выражать пределы допускаемой погрешности числом, которое остается одним и тем же для СИ одного уровня точности, но с различными верхними пределами измерений.
ГОСТ 8.401-80 предусматривает следующие формы выражения пределов основной погрешности СИ.
1. Пределы допускаемой абсолютной основной погрешности, выраженной в единицах измеряемой величины или условно в делениях шкалы, устанавливают по формуле
∆ = ± а; (1)
или
∆ = ±(а + bх); (2)
где ∆ – пределы допускаемой абсолютной основной погрешности, выраженной в единицах измеряемой величины на входе (выходе) или условно в делениях шкалы;
х – значение измеряемой величины на входе (выходе) СИ или число делений, отсчитанных по шкале;
|
|
|
а, b – положительные числа, не зависящие от х.
2. Пределы допускаемой приведенной основной погрешности устанавливают по формуле
 (3)
(3)
где Δ – пределы допускаемой абсолютной основной погрешности, устанавливаемые по формуле (1);
XN – нормирующее значение, выраженное в тех же единицах, что и Δ;
p – отвлеченное положительное число, выбираемое из ряда:
1·10 n; 1,5·10 n; 2·10 n; 2,5·10 n и т. д., где (n = 1; 0; –1, –2 и т. д.).
3. Пределы допускаемой относительной основной погрешности устанавливают по формуле
 если ∆ = ± а; (4)
если ∆ = ± а; (4)
или формуле
 если ∆ = ±(а + bх); (5)
если ∆ = ±(а + bх); (5)
где δ – пределы допускаемой относительной основной погрешности;
q – отвлеченное положительное число;
X к – больший (по модулю) из пределов измерений;
c и d – положительные числа, выбираемые из приведенного выше ряда
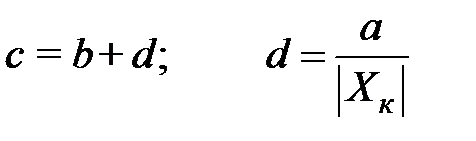 ,
,
а, b – числа, см. формулу (1). d характеризует аддитивную составляющую.
В обоснованных случаях пределы допускаемой относительной основной погрешности устанавливают по более сложной формуле или в виде графика либо таблицы.
Примеры нормирования основной погрешности при различном характере изменения основной погрешности показан в таблице.
| Δ = const; δ возрастает с уменьшением х | Δ возрастает с увеличением х; δ = const. | аддитивная и мультипликативная погрешности сопоставимые по величине |
| Нормируется: | Нормируется: | Нормируется: |
| ∆ = ± а | ∆ = ±(а + bх); (2) | |
 (3) (3)
| 
| 
|
| Стрелочные вольтметры и амперметры, АЦП (погрешность квантования) | Масштабные преобразователи: делители напряжения, шунты и т. п. | Цифровые вольтметры, омметры и др. |
1.8.2.2. Правила выбора нормирующего значения XN:
1. Для СИ с равномерной или степенной шкалой, а также для измерительных преобразователей, если нулевое значение входного (выходного) сигнала находится на краю или вне диапазона измерений, нормирующее значение устанавливают равным большему из пределов измерений. В данном примере нормирующее значение XN = 10.
|
|
|

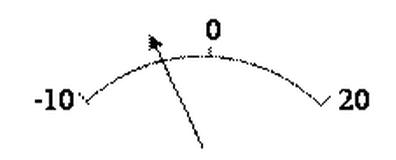
2. Если нулевое значение находится внутри диапазона измерений, то нормирующее значение берется равным большему из модулей пределов измерений, т.е. XN = 20.
3. Для электроизмерительных приборов с равномерной шкалой, практически равномерной или степенной шкалой и нулевой отметкой внутри диапазона измерений XN допускается устанавливать равным сумме модулей пределов измерений:
XN = | – 10| + |20| = 30.

4. Для средств измерений, для которых принята шкала с условным нулем (например, в градусах Цельсия), нормирующее значение устанавливают равным модулю разности пределов измерений, т. е. XN = |200 – 10| = 190.
Пример: Для милливольтметра термоэлектрического термометра с пределами измерений от 200 до 600 °С нормирующее значение ХN = 400 °C.
5. Для средств измерений с установленным номинальным значением нормирующее значение равно этому номинальному значению.
Пример. Для частотомеров с диапазоном измерений 45 - 55 Гц и номинальной частотой 50 Гц нормирующее значение ХN = 50 Гц.
6. Для измерительных приборов с существенно неравномерной шкалой (например, для омметров) нормирующее значение устанавливают равным всей длине шкалы или ее части, соответствующей диапазону измерений. В этом случае пределы абсолютной погрешности выражают, как и длину шкалы, в единицах длины.
|
|
|


