 |
16. Использование подземных пространств
|
|
|
|
Пещеры, я люблю ваш кров...
П. Ронсар
16. 1. Qui prodest - кому выгодно?
Этот обычный в судебной практике вопрос, ответ на который раскрывает мотивы поступков обвиняемых, нередко задают себе исследователи естественных и искусственных полостей. Наиболее полные сводки о возможностях использования подземных пространств (40-60 видов) опубликовали X. Триммель (1968), Г. А. Максимович (1972, 1974), Р. Скриванис (1990) и П. Ф. Швецов (1992). Системный анализ, выполненный под руководством автора студентами Симферопольского университета Ириной и Максимом Козловыми, выявил более 130 различных видов использования подземных пространств. Оказалось, что между использованием пещер и искусственных полостей нет принципиальных различий. Удобнее всего характеризовать их по сферам деятельности: промышленной, сельскохозяйственной, коммуникационной, военной, социальной, культовой и научной.
Промышленная сфера. Типы и виды использования полостей:
для добычи вмещающих пород (известняк, мел, каменная и калийная соли, песчаник и пр. );
добыча выполняющих отложений (кремень, медь, золото, железо, свинец, серебро, мышьяк, уран, драгоценные камни, мраморный оникс и пр. );
размещение заводов и объектов инженерного оборудования (железоплавильни, обогатительные фабрики, заводы точного приборостроения, ГЭС, АЭС, заводы по очистке воды, производству вина и пр. );
хранение различных веществ, материалов, продуктов производства (холодильные установки, нефтепродукты, отходы промышленности и пр. ).
Сельскохозяйственная сфера. Типы и виды использования полостей:
выращивание грибов (шампиньоны);
созревание сыров (рокфор и др. );
овощеводство (огурцы, томаты, лук, помидоры);
|
|
|
цветоводство (ландыши, жасмины, гвоздики, каллы и пр. );
пчеловодство (хранение ульев, пчеломатериалов и пр. );
добыча гнезд птиц (для еды и лечения);
загоны для скота (мелкий и крупный рогатый скот, домашняя птица);
скотомогильники.
Кроме того, из заполнителя полостей разных видов используются вода, гуано летучих мышей и птиц, костяная брекчия, гипс, мумие.
Коммуникационная сфера. Типы и виды использования полостей:
пути сообщения (пешеходные, велосипедные, железнодорожные, водные);
вокзалы, депо, стоянки автомашин;
коллекторы (водопроводы, газопроводы, водонесушие и водоотводящие коммуникации, электрические и телефонные кабели).
Военная сфера. Типы и виды использования полостей:
убежища и укрытия (мирные жители, военные, криминогенные элементы);
коммуникационные сооружения (пути сообщения, узлы связи, типографии и пр. );
фортификационные сооружения (укрепленные районы, бункера и пр. );
заводы (для производства оружия, боеприпасов и пр. );
полигоны (испытание оружия, стрельбища, места тренировок).
Из заполнителя полостей используются селитра (для производства пороха) и сталактиты (наконечники для стрел).
Социальная сфера. Типы и виды использования полостей:
жилье (города, убежища, тюрьмы);
водоснабжение (цистерны для сбора и хранения воды, колодцы);
склады (вино, фрукты, медикаменты, золотой запас, клады, послания потомкам и инопланетянам, мусор и пр. );
торговые помещения (магазины, рестораны, буфеты, мастерские, почта, телеграф и пр. );
лечебные цели (лечебницы разных профилей, а также отложения: мумие, гипс, мирабилит, галмей, гнезда стрижей, вода);
спортивно-экскурсионные цели (спортзалы, хоккейные поля, плавательные бассейны, учебные полигоны, спелеотуризм, экскурсии, танцевальные и концертные залы, музыкальные школы, проведение соревнований по спелеоориентированию, новогодние елки, фотографирование и пр. );
|
|
|
культурно-просветительные цели (горные, археологические, биологические, фармакологические, спелеологические музеи; библиотеки, архивы и пр. ).
Культовая сфера. Типы и виды использования полостей:
отправления культов (первобытные святилища, языческие капища, ведические, индуистские, исламские, иудейские, синтоистские, христианские храмы, часовни, церкви, мечети, монастыри);
отправления обрядов (инициация, бракосочетание, похороны и пр. ).
Научная сфера. Типы и виды использования полостей:
выяснение условий образования и существования полостей (маршрутные и стационарные геологические, гидрогеологические, микроклиматические, инженерно-геологические, биологические и прочие исследования);
изучение процессов, происходящих в земной коре и в космосе (геофизические наблюдения - наклономерные, деформографические, сейсмические, электромагнитные и др.; астрофизические наблюдения - изучение космических излучений, частиц больших энергий и пр. );
изучение жизни под землей (биологические наблюдения - жизнь животных в условиях вечной темноты, постоянной температуры и влажности; медицинские - изучение биоритмов человека при длительном пребывании под землей в спокойной и стрессовой обстановке, поведение человека и коллектива людей в условиях замкнутого пространства и информационной изоляции и пр. ).
Изучение пещерных пространств дает важные результаты не только в перечисленных, но и во многих других научных направлениях геологии (минералогия, седиментология и пр. ), гидрогеологии (изучение конденсации, особенностей движения подземных вод и формирования их гидрохимии, математики (проблемы топологии и пр. ).
Таким образом, использование подземных пространств полифункционально. Оно началось с палеолита и продолжается на протяжении всей истории человечества. К концу XX в. отмечается резкое увеличение видов и типов использования пещерных пространств, а также - увеличение количества используемых для разных целей объектов. Поэтому возникает проблема их оценки как ресурсов. В. Н. Андрейчук и Г. А. Бачинский считают пещерные пространства природными ресурсами особого типа; В. П. Коржик рассматривает их отдельные компоненты (горная порода, атмосфера, вода, биота) как специфические виды природных ресурсов. Приведенные данные свидетельствуют, что их нельзя в полной мере соотносить ни с одним из типов ресурсов, выделенных Н. Ф. Реймерсом.
|
|
|
Пещерные пространства - это интегральные ресурсы. Отдельные их типы (емкостные, газообразные, жидкие, твердые) в разных комбинациях входят в состав общих ресурсов: природных (пространственные, энергетические, литосферы, гидросферы, атмосферы, биосферы), трудовых (лечебные, познавательно-информационные, культурные, рекреационно-эстетические) и материальных (строительные, коммуникационные). Ресурсный подход к пещерным пространствам нуждается в выработке предложений и нормативов по их оценке, рациональному использованию и охране.
Наличие подземных пространств осложняет инженерно-строительное освоение территории. Если в 50-е гг. XX в. считалось, что естественные и искусственные полости оказывают влияние на устойчивость территории при глубине залегания до 20 м, то затем этот предел стал быстро увеличиваться. В настоящее время известны случаи их отрицательного влияния при глубине заложения 100-400 (Подмосковье, Приуралье, отдельные штаты США), а кое-где (Германия, Китай) - даже до 800-1000 м. Это заставляет по-новому подходить к геологической и экономической оценке территорий, где имеются пещеры и искусственные выработки.
Детальное рассмотрение возможностей использования подземных пространств уведет нас далеко в сторону. Поэтому остановимся только на нескольких из них, раскрывающих связи пещер с точными науками, археологическими и медико-биологическими проблемами.
16. 2. Сравнение не есть доказательство
В 1915 г. в Московском университете защищал магистерскую диссертацию " отец русского карстоведения" А. А. Крубер. Один из его оппонентов, профессор А. Лейст, задал " коварный" вопрос: как определялась глубина карстовых шахт, в которые никто не спускался? Ответ был кратким: " по времени падения камня". Но дотошный физик потребовал разъяснений. Они свелись к следующему. В шахте Монастыр-Чокрак звук от удара камня о дно слышен через 5 с после начала его падения. Так как камень падает равноускоренно, S = v0 + a*t2/2, где S - путь (глубина шахты, м); V0 - начальная скорость, м/с (равна нулю); t - время, с; а - ускорение свободного падения тел (9, 8 м/с2). Таким образом, S = 4, 9 t12 (t1 - время падения камня). Но звук в воздухе распространяется равномерно, со скоростью 330 м/с. Поэтому S = 330 t2. Получаем систему уравнений:
|
|
|
t1 + t2 = 5
4, 9 t2 = 330t2
из которых легко найти t1 и t2, а затем и S.
Глубина полости по расчету оказалась примерно равной 100 м. (Забегая вперед, отметим, что только в 1963 г. удалось проверить этот расчет прямым замером; глубина полости составила 90 м. ) Этим методом продолжали пользоваться до середины XX в. Еще в 1954 г. французский исследователь Ф. Тромб приводил в своей монографии " Спелеология" специальную таблицу, заменяющую расчеты. Но определить примерную глубину шахты - это лишь поставить задачу. Решить ее - значит спуститься на дно и благополучно выйти на поверхность. Вес спелеолога в полном снаряжении в среднем 90 кг. Сизальские, манильские и пеньковые веревки, которые использовались в конце XIX -начале XX вв., имели усилие на разрыв 385-1000 кг, что соответствует допустимой нагрузке 65-160 кг (1/6 разрывного усилия).
Положение осложнялось тем, что для подъема из шахты часто применялся " неподвижный блок" - веревка, переброшенная через ствол дерева. Согласно закону Эйлера, выведенному еще в начале XVIII в., в этом случае прилагаемая сила (Т, кг) больше веса спелеолога (Р, кг): Т = Р*ек*, где е - основание натуральных логарифмов, к - коэффициент трения (0, 35-0, 50), - угол охвата блока, рад. Для подъема через неподвижный блок приходится прикладывать усилие 150-180 кг. Именно поэтому при первых подъемах часто использовали лошадей. Таким образом, даже работая в статических условиях, веревки уже были на пределе крепости.
В середине XX в. сизаль и пенька были вытеснены из альпинизма и спелеологии более легкими и устойчивыми ко внешним воздействиям веревками из полиамида (капрон, нейлон, перлон), полиэстера (терилен), полипропилена и пр. Их разрывное усилие увеличилось до 1200-2400 кг. Однако применение новой техники (различные устройства для спуска и подъема) и тактики (использование одной или двух веревок, веревки и лестницы, веревки и троса и пр. ) поставило новые задачи. Пришлось разрабатывать более сложные формулы, учитывающие разные коэффиценты трения соприкасающихся материалов, изменяющуюся геометрию зажимных устройств, возникновение динамической нагрузки и пр.
В качестве примера приведем лишь формулу, используемую для определения разрывающего усилия веревки, Р, кг:
|
|
|
Р = М + (М2 + 4*M*H*W / L)0, 5,
где М - падающая масса, кг; Н - высота падения, м; W - предельная статическая нагрузка, кг; L - длина рабочего конца веревки, м. Для простейшего случая (М = 90 кг, Н = 5 м, W = 1500 кг, L = 50 м) величина Р достигает 250 кг...
Необходимо учитывать, что прочность веревок ощутимо снижается при хранении, увлажнении, загрязнении, длительном пребывании на солнце, завязывании узлов и пр. Оценить степень потери прочности (а, следовательно, и риска) можно только с использованием математики.
Но вот спелеолог на дне. Начата работа, первый и обязательный элемент которой - топографическая съемка. Она полностью основывается на геометрии и тригонометрии, а оценка ее результатов - на теории ошибок. Большинство топосъемок пещер по международной шкале имеет 3-й класс точности - создание съемочной сети без закрепления точек, измерение магнитных азимутов компасом, вертикальных углов - эклиметром, а расстояний - мерной лентой (с точностью до 1° и 10 см). Общая ошибка съемки крупной пещерной системы может достигать 4%. Это значит, что при расчетной глубине пройденной шахты 500 м ее истинная глубина может находиться в пределах 500±20 м. В практике отечественной спелеологии в 60-80 гг. было принято использовать меньшую величину. Именно поэтому шахта Киевская на массиве Кырк-Тау внесена в список крупнейших с глубиной 990 м, хотя имелись замеры 1030 и даже 1080 м. Позднее это было признано " перестраховкой", и в литературу проникли цифры типа 1508 м (шахта В. Пантюхина). Уж 8 метров здесь явно " от лукавого"...
Один из важнейших параметров карстовой полости, используемый затем в морфометрии, спелеометеорологии, гидрохимии, - ее объем. Определение объема элементарной геометрической фигуры, имеющей сечение в виде окружности, квадрата, треугольника или прямоугольника, трудностей не представляет. Но как быть в пещере, где эти сечения непрерывно чередуются, меняя свои размеры (длина, ширина, высота, радиус и пр. )? Оказывается, имеется универсальная формула Симпсона, обходящая все эти трудности /12/:
V = h/6(b1 + 4b2 + b3),
где V - объем полости, h - расстояние между сечениями, b1, b2, b3 - площади 1, 2 и 3 сечений. Единственное, что необходимо для расчетов, - набор данных о форме и размерах возможно большего числа сечений полости.
Современная спелеология имеет в своем арсенале и более точные методы. Например, чешские ученые разработали метод " щелевой" фотосъемки: лампа-вспышка, заключенная между двумя непрозрачными пластинами, " высвечивает" контур полости. Имея набор таких фотоснимков, увязанных между собой обычной топосъемкой, можно получить объем полости с ошибкой менее 15%, что вполне достаточно даже для инженерных изысканий.
Математика может пригодиться и при анализе особенностей заложения карстовых полостей. В Горном Крыму известно около 400 нивально-коррозионных колодцев и шахт, как помнит читатель, образованных тающим на их дне снегом. Они имеют разную глубину (Н, м), которая является функцией площади входа (S, м2):
H = 0, 5S + 7.
Итак, с глубиной " снежных" полостей все ясно. Но как они распределяются по глубине? Прежде всего, мы осреднили данные по 10-метровым интервалам и построили график-гистограмму (рис. 80 А).
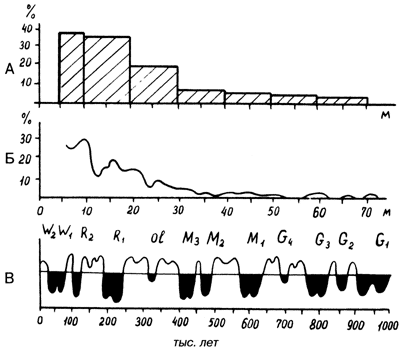
Рис. 80. Распределения нивально коррозионных полостей Горного Крыма. Распределение по глубине (А, Б) и смена оледенений-межледниковий в антропогене (В). А - гистограмма; Б - по истинным значениям; В - оледенения (черное) и межледниковья (белое)
Как и многие геологические процессы, распределение нивально-коррозионных полостей по глубине имеет логнормальный характер: максимум в интервале глубин 10-20 м и закономерное убывание количества полостей к 70-80 м. Через десяток лет возникла идея: что мешает нам построить не гистограмму, а диаграмму, с шагом по глубине 1 м? Неожиданно возникла многовершинная (многомодальная) кривая с 12 пиками (рис. 80 Б). Попытки расчленить ее на более простые распределения, учесть размещение полостей на разных массивах, высоту их заложения, литологию карстующихся пород, количество выпадающих осадков и т. д. результата не дали. На всех " частных" графиках упрямо возникали эти же 12 пиков... Загадочные кривые надолго легли в один из ящиков стола.
Ответ пришел неожиданно. Перелистывая " Реферативный журнал", мы натолкнулись на кривую оледенений-межледниковий, составленную итальянским геоморфологом Ч. Эмилиани. " Стоп, - сказало подсознание, - такое мы уже видели".
Но где? Конечно же, на графике в ящике стола. Сравнение материалов показало их удивительное сходство. Для подтверждения его пришлось использовать более современную палеоклиматическую кривую В. А. Зубакова, построенную с учетом периодичности колебаний земной орбиты, и довольно тонкий математический аппарат. Особенно хорошо совпали пики, соответствующие оледенениям рисс-2, рисс-1, миндель-3, миндель-1, гюнц-4 и гюнц-3. Несколько хуже фиксировались оледенения глюч, миндель-2, гюнц-2. Пики, не имеющие аналогов в оледенениях, соответствуют климатическим минимумам межледниковых периодов. Таким образом, интенсивность образования карстовых полостей нивально-коррозионного класса увязывается с климатическими ритмами третьего порядка, проявляющимися в чередовании ледниковых и межледниковых эпох, обусловленном колебаниями количества и состава солнечной радиации /21/. Вот как глубоко завели нас совсем небольшие и неинтересные для спелеолога нивально-коррозионные колодцы и шахты!
Космические ритмы давно фиксируются в спилах древесных стволов в виде чередования колец разной толщины. Появилась даже специальная наука - дендрохронология, а лучшими " гидами в прошлое" считались деревья-долгожители - североамериканская секвойя или туркестанская арча, возраст которых достигает 2 тысяч лет. По ним созданы дендрошкалы, с помощью которых удается с точностью до 1 года определить возраст каждого кольца. Однако А. Е. Ферсман еще в 1915 г. отмечал, что их аналогами являются годовые кольца сталактитов. Но, в отличие от деревьев, они могут на длительное время прекращать свой рост или даже подвергаться растворению. Это приводит к " выпадению" листков подземного календаря. Поэтому специалисты с большим интересом встретили сообщение крымских спелеологов о нахождении в русле подземной реки Краснопещерной естественных плотин-гуров, выросших прямо в потоке воды. Их рост никогда не прерывался, а количество сезонных слойков превышало 10 тысяч.
Расшифровка ритмограмм в трех натечных плотинах позволила выявить ритмы второго порядка протяженностью около 1800 лет, связанные с колебаниями общей увлажненности материков, и большое количество 11-летних ритмов, подчиняющихся гармоническим колебаниям солнечной активности. Компьютерная расшифровка ритмичности строения гуров пещер Европы и других материков - космической летописи за 10-12 тысяч лет - дело будущего.
Более мелкие космические ритмы оказывают влияние на гидрогеологию карстовых массивов, определяя некоторые особенности спелеогенеза (формирования пещер). Приливы и отливы лунно-солнечной природы прослежены не только в Мировом океане, но и на суше, в земной коре, от экватора до 50-60° северной и южной широты. Они приводят к полусуточной пульсации воды в карстовых сифонах, а на большой глубине, в зоне замедленного движения карстовых вод, вызывают расширение трещин и пор за счет коррозии смешивания (" выжимание" воды из пор в трещины во время приливов и их обратное " засасывание" при отливах). Суточный эффект этого процесса ничтожно мал. Но природа нетороплива: его повторение на протяжении миллионов лет приводит к формированию полостей там, где вроде бы их быть не должно...
В гидрологии имеется понятие " выработанный профиль", или " профиль равновесия". Это теоретическая кривая, которой стремится достичь всеми своими точками реальный водоток. Она очень крутая в верхней, более пологая - в средней и совсем пологая - в нижней части. Описывает ее уравнение y = а*евх, где х - расстояние от истоков, у - высота над уровнем моря, е - основание натуральных логарифмов, а и в - числовые коэффициенты.
Спелеологи давно обратили внимание на то, что подземные водотоки состоят из чередующихся участков наклонных, иногда меандрирующих галерей разной длины и соединяющих их вертикальных колодцев или шахт разной глубины. Казалось бы, никакого порядка! Но итальянский спелеолог Г. Абрами в 1968 г. выдвинул смелое предположение: может быть, подземные водотоки подчиняются той же закономерности? После публикации Атласа крупнейших пещер мира /35/ возникла возможность проверить эту гипотезу. 28 полостей, расположенных в Пиренеях, Альпах, Динаридах, Крыму и на Кавказе, легли днищами колодцев на теоретическую кривую (рис. 81). Определив ее числовые коэффициенты для данного карстового массива, спелеологи получили возможность предсказывать, как поведет себя полость дальше: ждать ли за сифоном наклонных, затопленных водой ходов, или готовить снаряжение для преодоления следующих колодцев... Хорошо " работает" этот метод и для предсказания сухих продолжений в верхней части карстовых систем. Кроме того, выяснилось, что вертикальные элементы карстовых систем хорошо коррелируются с этапами поднятий массива, что очень заинтересовало тектонистов и палеогеографов.
Не обойтись без математики и при определении " спелеологического потенциала" разных карстовых районов. Сведения о количестве пещер в разных странах мира противоречивы. По данным X. Триммеля (1968), во Франции и в Италии внесено в кадастры более 10 тыс. полостей, в США - более 13-ти. Эти данные очень быстро устаревают. Кроме того, многое зависит от точки отсчета. В большинстве регионов бывшего СССР кадастры полостей включали объекты протяженностью или глубиной 10 м и более. После того как на Урале " порог" учета был снижен до 5 м, количество полостей в этом регионе сразу возросло с 670 (1980 г. ) до 1870 (1993 г. ).

Рис. 81. Реальный профиль карстовой водоносной системы и кривая предельного равновесия, рассчитанная по днищам карстовых колодцев.
К счастью для спелеологов будущего века, даже в хорошо изученных регионах сегодня далеко не все пещеры открыты и исследованы. Сколько осталось таких неоткрытых полостей? Ответ на этот вопрос попытался дать американский спелеолог и химик Р. Кирл. Пусть в данном районе имеется 1 полость с пятью входами, 2-е четырьмя, 5 - с тремя, 26 - с двумя и 774 - с одним. Построив кривую их распределения и " спрямив" ее, применив полулогарифмический график, можно экстраполировать имеющиеся данные в область неизвестных пещер (с " нулем" входов). Для Горного Крыма их должно быть 1740. То есть сегодня нам известно только 35% от общего числа существующих полостей...
Спелеологам как представителям естественных наук часто приходится сравнивать между собой разные объекты: отдельные пещеры, их форму, размеры, микроклимат, обводненность. Но недаром французский математик Араго говорил: - сравнение не есть доказательство... Если подключить математику, достоверность выводов значительно повышается. Приведем лишь два примера.
В 60-е гг. были начаты исследования гипсовых лабиринтов Подолии (Украина). Понимая, что механизм их образования существенно отличается от крымского, автор предложил переточную модель: вода поглощается в бортах и днище одного притока Днестра и перетекает под водоразделом в долину смежной, более глубоко врезанной реки. Моделью для этой гипотезы послужила пещера Вертеба, расположенная в шейке меандра р. Серет и явно образованная при частичной потере стока этой крупной реки. Выдвинутая идея была подтверждена наблюдениями геофизиков: электроразведочными работами на предполагаемых путях перетока были обнаружены продолжения пещеры, заполненные глинистым материалом.
В 90-е гг. А. Климчук предложил обоснованную новыми фактическими данными артезианскую модель гипсового спелеогенеза. Пещеры прорабатываются не сверху или сбоку, а снизу, за счет подтока менее минерализованных напорных вод. Она убедительно объясняла многие особенности пещер Подолии, что, однако, не означало необходимости полного отказа от " переточного" механизма. По новейшим данным, приведенным в работе А. Климчука " Гипсовый карст мира" (1997), тринадцать пещер Подолии имеют коэффициент объемной закарстованности 0, 002-0, 007, а четырнадцатая (Вертеба) - 0, 120. Возникает сомнение: а относится ли она к генеральной совокупности (то есть к группе пещер, имеющих артезианский генезис). Для проверки используем t-критерий:
= (х - хср)/,
где х - текущее, a xср - среднее значение коэффициента объемной закарстованности, - его среднее квадратическое отклонение. Расчет дает величину = 2, 3. Но для выборки из 14 членов нормированное отклонение а составляет 2, 6. Так как а < (2, 6 < 2, 3), сомнительное значение коэффициента объемной закарстованности (0, 120) не входит в генеральную совокупность. Это означает, что для пещеры Вертеба артезианская модель не подходит.
Второй классический пример касается сравнения двух выборок. При исследовании группы Воронцовских пещер на Кавказе в 50-е гг. были отобраны по три пробы инфильтрационной воды, имеющие минерализацию 100, 200 и 300 мг/л (пещера А) и 200, 400 и 600 мг/л (пещера Б). Сделан вывод, что вода из пещеры Б имеет в два раза более высокую среднюю минерализацию, чем из пещеры А (400 и 200 мг/л). Однако при малом объеме выборки сравнивать средние без дополнительной проверки опасно. Если число наблюдений заключено между 3 и 10, то для сравнения выборок следует использовать tQ -критерий:
tQ = (|Xcp1 - Xcp2|) / [(Q1 - Q2) / (n1 - n2 - 4) * (1/n1 + 1/n2)]0, 5 > = 2,
где Q1 = (хi-хср)2; Q2 = (хi-хср)2.
Выполнив вычисления, получаем tQ = 1, 4 < 2, то есть между пробами из пещер А и Б нет различий. Они принадлежат к одной генеральной совокупности с xср =300 и = 178... Так математика страхует спелеолога от ошибочных выводов.
Читатель, естественно, понимает, что мы привели только самые простые примеры применения математики, свидетельствующие о ее возможностях. В разных случаях используются более сложные приемы обработки материалов и более мощные критерии оценки их результатов.
16. 3. Магическая семерка
Еще совсем недавно развитие астрономии как науки связывалось с древнейшими земледельческими цивилизациями. Отдельные находки свидетельствовали о том, что охотники, собиратели, рыболовы разных частей света умели ориентироваться по небесным светилам, связывали сезонные изменения в природе с появлением определенных животных и т. д. Американский исследователь А. Маршак именно так интерпретировал рисунок кузнечика, выгравированный на кости мамонта из пещеры Трех Братьев (рис. 82): прискакал кузнечик - жди тепла!
В 30-е гг. XX в. чешский археолог К. Абсолон обратил внимание на частое повторение числа 5 в рядах зарубок, надрезов, штрихов, из которых состояли узоры на различных предметах из пещер Дольни Вестонице, Пшедмости и пр. (Моравия). Значение этих находок оценили не сразу, но в 1938 г. историк математики Дж. Сартон включил " счетную палочку" из Вестонице в перечень древнейших доказательств становления счета у первобытного человека. Позднее выяснилось, что кроме 5 (число пальцев на руке) на предметах их пещерных стоянок упорно повторяется число 4 (четыре стороны света, четыре ветра), давшие начало четырехконечному кресту и двадцатеричному (5*4) счету индейцев Америки. Значительно реже встречается более древняя (пещера Пеш дель-Азе, Франция, 300 000 лет) троичная система (3-6-9), которой пока нет убедительных природных или этнокультурных объяснений.
В 60-е гг. появились первые публикации о наличии на предметах разного рода из палеолита (бивни мамонта, рога оленя, пряжки, статуэтки, рисованные композиции из пещер Ласко, Альтамира, Гранде, Вертеш) ритмически повторяющихся ямок и нарезок, состоящих из 7-14 элементов. Использовав методы статистического анализа, историк Б. Фролов доказал, что число 7 с удивительным постоянством проявляется в орнаментах, мифах, обрядах, фольклоре народов, живших в разное время и в разных районах Земли. На 7 зон по значимости делятся палеолитические пещеры, семь линий или ямок обязательно присутствуют в орнаменте, нанесенном на женские статуэтки...
Детальный анализ выявил еще более удивительные закономерности. Черточки, нанесенные под углом к краю орнаментированного предмета, объединяются в группы (7 + 7 = 14), а затем меняют направление наклона; каждая " двойная" группа соответствует одному и тому же природному явлению - нарастанию диска Луны до полнолуния и убыванию его до новолуния в течение 28-29 дней. При достаточно больших размерах орнамента (на браслете, бивне мамонта и пр. ) на нем наносятся десять двойных групп. Так выглядит архаичная форма первобытного календаря, связанного с 10 лунными месяцами продолжительности беременности. Это подтверждается наличием рисунков, непосредственно изображающих фазы Луны (пещера Канчал де Маома, 8-7 тыс. лет до н. э. ).
Теперь становятся понятными и некоторые другие рисунки первобытного человека. Во многих пещерах (заметим - и во многих более поздних мифах! ) очень часты композиции, объединяющие быков и женские знаки (точки, округленные ромбы, треугольники, направленные вершиной вниз). Ключом к теме является одинаковый календарный срок беременности!
Не меньшую роль в формировании астрономических познаний палеолитического человека играло и Солнце. Смена сезонов года, происходящая примерно за 360 дней, сопоставляется со сроком беременности кобыл и ослиц. Может быть, именно поэтому рисунки лошади занимают первое место по численности? Солнечный год находит отображение не только в рисунках, но и в орнаментах: на многих из них к 282 черточкам (10 лунных месяцев) симметрично добавляются еще по 42, что дает 366 дней (солнечный год).
В древнешумерийской поэме, записанной на 12 глиняных табличках (3 тыс. до н. э. ), повествуется о подвигах полумифического царя Гильгамеша. Разные эпизоды поэмы отражают чередование времен года и соответствуют названиям созвездий. Десятый месяц называется месяцем " Пещеры восходящего солнца". Исследования А. Маршака показали, что необходимый для земледелия комплекс знаний о периодичности природных процессов на Земле и их связях с небесными явлениями сложился уже 10 тыс. лет назад. Затем он непрерывно совершенствовался с учетом новых потребностей.
А. Гурштейн предположил, что следующим этапом формирования астрономических знаний первобытного человека было выделение в поясе Зодиака четырех особых точек: весеннего и осеннего равноденствия (уравнивание светлого и темного времени суток) и летнего и зимнего солнцестояния (высшей и низшей полуденной высоты Солнца над горизонтом). Это требует наблюдений за перемещениями Солнца на протяжении года и " закрепления" его положения среди созвездий. Первые представления о " квартете", включающем современные созвездия Близнецов (символ рождения новой жизни), Девы (символ лета), Стрельца (символ осени) и Рыб (символ зимы), судя по археологическим находкам из пещер, сформировались еще в 8-4 тысячелетиях до нашей эры.
Таким образом, сакрализация числа 7 (отнесение его к определенному религиозному ритуалу) произошла еще в позднем палеолите. Она имеет астрономическую (фазы Луны) и биологическую (продолжительность беременности) природу. Но возможно, в чем-то правы и современные психологи, которые доказали ограниченность оперативных возможностей человека 7 однотипными единицами восприятия, памяти, действий...
Итак, находки в пещерах помогли специалистам разобраться в путях и методах формирования первичных астрономических знаний человека. Чтобы сделать следующие шаги, ему необходимо было перейти к систематическим наблюдениям. Так появились пещеры-обсерватории.
16. 4. Подземные обсерватории
Возникновение астрономии связано с ранней историей развития человеческого общества. Охота, скотоводство, позднее - торговля требовали умения ориентироваться в пространстве. Еще в незапамятные времена было замечено, что два раза в год Солнце всходит и заходит в определенных точках на востоке и западе, а отдельные яркие звезды в течение ночи совершают оборот вокруг некоторой точки. Такие периодические явления, как фазы Луны, смена дня и ночи, дали начало календарю. По этому поводу имеется огромная специальная литература, из которой выделим лишь некоторые моменты, связанные с пещерами.
На стенах многих пещер имеются " сезонные" рисунки - изображения змей, рыб, птиц, растений (рис. 82). В пещере Чокурча под Симферополем краевед А. Столбунов в 1979 г. нашел лопаточную кость мамонта со множеством нанесенных на нее точечных изображений (11-10 тыс. до н. э. ). Астроном В. М. Чернов определил, что на ней изображен участок звездного неба северного полушария, на котором удалось отождествить 16 созвездий (Северная Корона, Гончие Псы, Волопас, Дева и пр. ) и 102 звезды.
В 1987 г. болгарские спелеологи провели археологические исследования в небольшой пещере Байловского комплекса. На ее стенах обнаружены и изображения фаз Луны, выполненные черной органической (гуано летучих мышей) и лиловой минеральной красками. Возраст изображений восходит к 3 тыс. до н. э. Предполагается, что это первая в мире " школа" жрецов. Изображения фиксируют календарную последовательность выполнения ритуалов, определяемую положением Солнца и Луны. Астрономическая символика (астральные и солярные знаки, календари, композиции с космологическим содержанием) обнаружены во многих пещерах Болгарии.
В районе Дублина (Ирландия) находится сложенная из камней гробница (3 тыс. до н. э. ). В день зимнего солнцестояния через отверстие в ее передней стене луч восходящего солнца освещает ритуальные знаки, нанесенные на ее заднюю стенку.
При раскопках в одной из пещер Китая найден панцирь черепахи, датируемый по другим находкам XIV в. до н. э. На нем иероглифами записано сообщение о появлении на небе новой яркой звезды. Сейчас на этом месте находится источник гамма-излучения. Так что это, вероятно, самое древнее сообщение о вспышке Сверхновой.
На острове Наксос (Эгейское море) А. Петрохилос обнаружила много пещер и гротов с астральными знаками (1 тыс. до н. э. ). Среди них выделяются спирали, символизирующие смену зимы летом, зодиакальные знаки и пр.
А. Нуньес-Хименес описал несколько пещер Кубы и Венесуэлы с концентрическими красными и черными кругами (1 тыс. до н. э. ), олицетворяющими день и ночь. Некоторые круги перечеркнуты стрелой, направленной в сторону восхода солнца.
В 1054 г. вспыхнула Сверхновая звезда (на ее месте сейчас находятся Крабовидная туманность и оптический пульсар). Это феерическое событие наблюдали китайские астрономы, о чем рассказано в летописях, найденных в пещерах. Но его видели и индейцы Северной Америки. В пещере Галас (Нью-Мехико) в 1990 г. обнаружены глиняные чаши, расписанные изнутри. На них часты изображения Кролика, символизирующего Луну. На одной из чаш скрючившийся Кролик держит в лапе круглый предмет с исходящими из него лучами. Взаимное положение Сверхновой и серпа Луны соответствует наблюдениям китайских астрономов.
Это же событие отражено на скальной плите в вулканической Папоротниковой пещере (Калифорния). Древний художник почти без искажений изобразил участок звездного неба со звездами Альтаир, Вега, Арктур, Спика, Антарес, Регул, серп Луны и Сверхновую в созвездии Тельца. Американский астроном Р. Престон считает, что пещерные обсерватории в Калифорнии (XII-VII вв. до н. э. ) являются аналогом " наземных обсерваторий" (1 тыс. до н. э. ), которых много в пустыне Аризона. Имеется даже проект поиска изображений Сверхновых на стенах пещер, с тем чтобы пополнить имеющиеся данные об этом редком явлении (1700 г. - Кассиопея А, 1604 г. - Кеплера, 1572 г. - Тихо Браге и пр. ).
В пещерном монастыре Красен (Болгария) имеется келья, в стене которой пробито овальное отверстие со средним диаметром 30 см. По расчетам, в XIII в. н. э. солнечный луч освещал икону, расположенную на противоположной стене кельи, только два раза в год: в Сретенье (2 февраля) и в Преображение (6 августа). Так в монастыре действовала астрономическая система, позволяющая точно определять наступление весны и церковного праздника, связанных с ожиданием богатого урожая в конце года.
К пещерным изображениям обращаются и в конце XX века. Французский ученый А. Лот считает, что фрески грота Тасилли (Сахара) изображают живых существ в скафандре. Такой же рисунок найден в Японии. Возраст их одинаков - около 5 тыс. лет. Во многих пещерах Франции и Испании (Трех Братьев, Нио, Альтамира) найдены наскальные рисунки, напоминающие неопознанные летающие объекты. Так ли это? Кто знает...
Таким образом, пещеры являются настоящей " каменной библиотекой", хранящей астральные и космические представления человечества, переплетающиеся с его повседневной, земной деятельностью. Э. Тайлор /26/ на обширном этнографическом материале проследил связь движения Солнца с загробным миром: " В силу самого простого поэтического сравнения с ежедневно восходящим и заходящим солнцем, олицетворяющим человеческую жизнь в прелести рассвета, в блеске полудня и в


