 |
Математическая постановка транспортной задачи.
|
|
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
КАЗАХСКИЙ ГОСУДАРСТВЕННЫЙ ЖЕНСКИЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА ИНФОРМАТИКИ
Дипломная работа
ПО ТЕМЕ:
«Решение транспортной задачи линейного программирования в среде MS Excel»
Выполнила: студентка 4курса,
протокол № о/о, р/о, спец. «Информатика»
Оспанова А.А.
Научный руководитель:
к.т.н., доцент старший преподаватель
Г.И. Салгараева Мусиралиев Ж.А.
Алматы 2008 г.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
Глава I Задачи линейного программирования
1.1 Общая характеристика задачи линейного программирования
1.2 Математическая постановка задачи линейного программирования
Глава II Основные методы решения транспортной задачи линейного программирования
2.1 Математическая постановка транспортной задачи
2.2 Решение транспортной задачи с помощью программы Ms Excel
2.3 Рекомендации по решению задач оптимизации с помощью надстройки «Поиск решения»
Глава III Двойственная задача линейного программирования
Математическая формулировка двойственной задачи линейного программирования
3.2 Математическая постановка двойственной задачи о красках
3.3 Решение двойственной задачи о красках с помощью программы Ms Excel
Заключение
Литература
Введение
Транспортная задача.
В некотором географическом регионе имеется фиксированное число пунктов производства и хранения некоторого однородного продукта и конечное число пунктов потребления этого продукта. В качестве продукта может выступать, например, нефть, уголь, песок, цемент, т.д. Для каждого из пунктов производства и хранения известен объем производства продукта или его запаса. Для каждого пункта потребления задана потребность в продукте в этом пункте потребления.
|
|
|
Требуется определить оптимальный план перевозок продукта, так чтобы потребности во всех пунктах потребления были удовлетворены, а суммарные затраты на транспортировку всей продукции были минимальными.
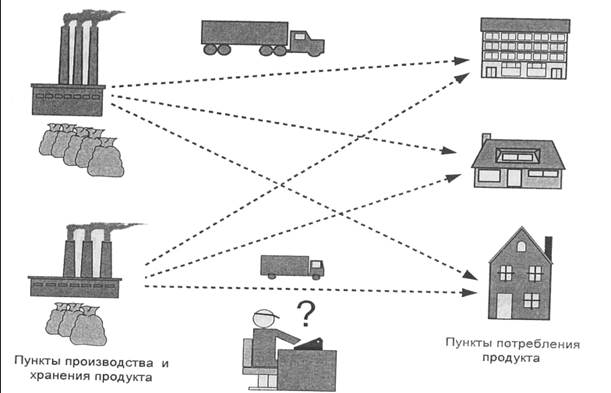
Рисунок1. Иллюстрация транспортной задачи для двух пунктов производства и трех пунктов потребления
Очевидно, оценочной функцией в данной задаче являются суммарные затраты на транспортировку всей продукции, а ограничениями служат объемы производства и потребности в продукте в каждом пункте потребления.
Данная задача также является одной из классических задач линейного программирования, методы ее решения мы будем рассматривать далее. В бизнес приложениях эта задача известна как задача о перемещении товаров со складов на торговые точки или задача о планировании цепочек поставок. В случае штучного товара, например, телевизоры, компьютеры, пылесосы, автомобили и пр., соответствующая транспортная задача относится к классу задач целочисленного программирования.
Транспортная задача: Уменьшение затрат на перевозку.
В этой работе мы рассмотрим решение классической транспортной задачи Excel 7.0 позволяет находить оптимальное решение, сохраняя заданные ограничения.
Транспортная задача является классической задачей исследования операций. Множество задач распределения ресурсов сводятся именно к этой задаче.
Математическая постановка транспортной задачи.
Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из т пунктов отправления А1,А2,…,Ат в п пунктов назначения В1,В2,..,Вп. При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза. Обозначим через сij тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, через ai-запасы груза в j-м пункте отправления, через bj-потребности в грузе в j-м пункте назначения, а через xij-количество единиц груза, перевозимого из i-го пункта отправления в j-й пункт назначения. Тогда математическая постановка задачи состоит в определении минимального значения функции:
|
|
|
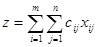, [1]
при условиях:
[2]
[3]
[4]
Поскольку переменные 
удовлетворяют системам уравнений(2) и (3) и условию неотрицательности (4), то обеспечивается доставка необходимого количества груза в каждый из пунктов назначения (условие (2)), вывоз имеющегося груза из всех пунктов отправления (условие (3)), а также исключаются обратные перевозки (условие (4)).
Определение 1. Всякое неотрицательное решение системы линейных уравнений (2) и (3), определяемое матрицей Х=(
) (i=1,…m;j=1,…n), называется планом транспортной задачи.
Определение2. План 
=(
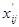) (i=1,…m;j=1,…n), при котором функция (1) принимает своё минимальное значение, называется оптимальным планом транспортной задачи.
Обычно исходные данные транспортной задачи записывают в виде (см. таблицу 1.)
Очевидно, общее наличие груза у поставщиков равно:
,
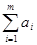а общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т.е.
единиц.
Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т.е.
= , [5]
То модель такой транспортной задачи называется закрытой. Если же указанное условие не выполняется, то модель транспортной задачи называется открытой.
Таблица 1
Теорема 1. Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения, т.е. чтобы выполнялось равенство (5)
| Пункты отправления | Пункты назначения | Запасы | ||||
| … | 
| … | 
| ||
| 
| 
| 
| 
| ||
| … | … | … | … | … | … | … |
| 
| 
| 
| 
| ||
| … | … | … | … | … | … | … |
| 
| 
| 
| 
| ||
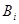
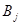
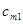
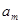
| Потреб ности | 
| … | 
| … | 
| |
В случае превышения запаса над потребностью
> 
,
вводится фиктивный (n+1)-й пункт назначения с потребностью
= -
|
|
|
и соответствующие тарифы считаются равными нулю: 
=0 (i=1,…m). Полученная таким образом задача является транспортной задачей, для которой выполняется равенство (5).
Аналогично, при
< ,
вводится фиктивный (m+1)-й пункт отправления с запасом груза
= -
и тарифы пологаются равными нулю: 
=0 (j=1,…m). Этим задача сводится к обычной транспортной задаче, из оптимального плана которой получается оптимальный план исходной задачи.
Число переменных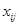 
в транспортной задаче с m пунктами отправления и пунктами назначения равно m n, а число уравнений в системах (2) и (3) равно n+m-1. Следовательно, опорный план транспортной задачи может иметь не более n+m-1 отличных от нуля неизвестных.
Если в опорном плане число отличных от нуля компонент равно в точности n+m-1, то план является невырожденным, а если меньше-то вырожденным.
Для определения опорного плана существует несколько методов. (Как и для всякой задачи линейного программирования, оптимальный план транспортной задачи является и опорным планом). Для определения оптимального воспользуемся средством Поиска решений, реализованного в Excel.
Допустим, что ваша фирма занимается переработкой некоторого сырья на нескольких заводах (потребители-З1,З2,…), расположенных в разных районах города. Сырье поставляется со складов (поставщики-П1,П2,…), расположенных в нескольких городах области. Стоимость сырья одинаковая, однако, перевозка со склада и завода. Потребность заводов в сырье различна, и запасы на каждом складе ограничены. Требуется определить: с какого склада, на какой завод поставлять, сколько сырья для минимизации общих затрат на перевозку.
В нашем примере обозначим заводы З1,З2,З3,З4, а склады П1,П2,П3,П4,П5. Стоимость перевозки измеряется в тенге на тонну груза, а потребность заводов и складские запасы - в тоннах.
|
|
|
