 |
линейного программирования
|
|
|
|
В общем случае двойственной по отношению к стандартной задаче линейного программирования (1.6) и (1.7) называется такая задача линейного программирования, которая может быть записана в следующем виде:
b1y1+b2y2+,…,+bmym →  (3.1)
(3.1)
где множество допустимых альтернатив  формируется следующей системой ограничений типа неравенств:
формируется следующей системой ограничений типа неравенств:
 (3.2)
(3.2)
и y1,y2,,…,yn  0.
0.
Как не трудно заметить, количество переменных двойственной задаче линейного программирования равно количеству ограничений стандартной задачи, а количество ограничений двойственной задачи равно количеству переменных стандартной задачи линейного программирования. При этом, если исходная задача формулируется как задача максимизации целевой функции, то двойственная- как задача минимизации и наоборот. Аналогично изменяются и знаки ограничений двойственной задачи по отношению к исходной задаче линейного программирования.
Существует важная взаимосвязь между двойственной и стандартной задачами линейного программирования. А именно, если одна из задач (1.6) и (1.7) или (3.1) и (3.2) имеет оптимальное решение, то и двойственная ей задача линейного программирования имеет оптимальное решение, при этом оптимальные значения соответствующих целевых функций двойственных задач имеют равные значения, т.е. f’op=fopt, где f’(y)- целевая функция в выражении (3.1), а f(x)–целевая функция в выражении (1.6). Если же для одной из задач (1.6) и (1.7) или (3.1) и (3.2) целевая функция не ограничена на допустимом множестве альтернатив, то соответствующая ей двойственная задача линейного программирования не имеет решения, т.е. имеет множество допустимых альтернатив. Наконец, если одна из задач (1.6) и (1.7) или (3.1) и (3.2) имеет пустое множество допустимых альтернатив, то соответствующая ей двойственная задача линейного программирования либо имеет неограниченную целевую функцию, либо пустое множество допустимых альтернатив.
|
|
|
В общем случае совместное рассмотрение пары двойственных задач линейного программирования позволяет не только выполнить качественный анализ их решения, но и практически использовать найденное решение одной из них для более простого решения другой задачи. Хотя данное свойство оказывается полезным, главным образом, при выполнении ручных расчетов, далее рассмотрим процесс решения двойственных задач линейного программирования с помощью программы MS Excel применительно к задаче о красках.
3.2 Математическая постановка двойственной задачи о красках
Напомним, что исходная постановка задачи о красках сформулирована в форме (3.1) и (3.2). двойственная к ней задача линейного программирования после выполнения простейших преобразований с целью получения целочисленных коэффициентов целевой функции и ограничений может быть записана в следующем виде:
100y1+70y2+100y3→  (3.3)
(3.3)
где множество допустимых альтернатив  формируется следующей системой ограничений типа:
формируется следующей системой ограничений типа:
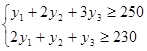 (3.4)
(3.4)
и y1,y2,y3  0.
0.
3.3 Решение двойственной задачи о красках
с помощью MS Exsel
Для решения двойственной задачи о производстве красок с помощью программы MS Exsel создадим новый рабочий лист с именем Двойственная задача. Далее необходимо выполнить следующие действия:
1. Внесем необходимые записи в ячейки А1:Е1, А2:А6, Е4:F4. Следует отметить, что конкретное содержание этих надписей не оказывает никакого влияния на решение рассматриваемой двойственной задачи линейного программирования.
2. В ячейки B2:D3 введем значения коэффициентов целевой функции (3.3) b1=10, b2=7, b3=5.
3. В ячейку E2 введем формулу: =суммпроизв(В2:D2; B3:D3), которая представляет целевую функцию (3.3).
|
|
|
4. В ячейки B5:D6 введем значения коэффициентов ограничений (3.4.).
5. В ячейки F5:F6 введем значения правых значений ограничений (3.4.).
В ячейку E5 введем формулу: =суммпроизв($В$2:$D$2; B5:D5), которая представляет левую часть первого ограничения (3.4).
Рисунок 3.1 Исходные данные для решения двойственной
|
7. Скопируем формулу, введенную в ячейку Е5, в ячейку Е6.
Внешний вид рабочего листа MS Office Excel 2003 с исходными данными для решения задачи об оптимальном рационе питания имеет следующий вид рисунок 3.1.
Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию главного меню: Сервис|Поиск решения.
После появления диалогового окна Поиск решения следует выполнить следующие действия:
1. В поле с именем Установить целевую ячейку: ввести абсолютный адрес ячейки $Е$2.
2. Для группы Равной: выбрать вариант поиска решения- минимальному значению.
3. В поле с именем Изменяя ячейки: ввести абсолютный адрес ячеек $В$2:$D$2.
4. Добавить три ограничения, соответствующие (3.5), и одно ограничение на допустимые значения переменных.
5. В дополнительном окне параметров поиска решения следует выбрать отметки Линейная модель и Неотрицательные значения рисунок 3.2.
 |
Рисунок 3.2. Ограничения на значения переменных и параметры мастера поиска решения для двойственной задачи о красках
После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать Выполнить. После выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет следующий вид рисунок 3.3.
Рисунок 3.3 Результат количественного решения
двойственной задачи о красках

Рисунок 3.4. Отчет по результатам
 |
Результатом решения двойственной задачи о производстве красок являются найденные оптимальные значения двойственных переменных: у1=70, у2=90, у3=0,которымсоответствует значение целевой функции: f’opt=13 300. При выполнении расчетов для ячеек был выбран числовой формат с тремя знаками после запятой.
Одним из наиболее важных свойств двойственных задач является наличие в симплекс-таблице, соответствующей оптимальному решению одной из них, значений оптимального решения двойственной задачи. Применительно к задаче о красках, значения оптимального решения двойственной задачи о красках (3.3) и (3.4) можно сразу получить из последней симплекс-таблицы. А именно, оптимальное решение двойственной задачи содержится в индексной строке в столбцах, соответствующих дополнительным переменным х3,х4,х5.поскольку переменная х3 вводится в первое ограничение прямой задачи, которому, в свою очередь, соответствует первая переменная у1 двойственной задачи, то из табл. непосредственно следует оптимальное значение для у1=хf3=70.
|
|
|
Аналогично могут быть получены и значения у2=хf4=90 и у3=хf5=0. При этом нет никакой необходимости в непосредственном решении двойственной задачи.
Экономическая интерпретация полученных решений прямой задачи двойственной задач заключается в следующем. Решение прямой задачи о красках (4.3.1) и (4.3.2) дает оптимальный план производства красок первого и второго вида. Решение двойственной задачи о красках (3.3) и (3.4)- оптимальную систему оценок типов сырья, используемого для производства этих красок. При этом выполняются следующие условия. Если некоторый тип сырья используется полностью, то соответствующая этому типу двойственная переменная в оптимальном решении двойственной задачи будет иметь положительное значение. Если же некоторый тип сырья используется не полностью, то соответствующая этому типу двойственная переменная в оптимальном решении двойственной задачи будет равняется нулю.
Применительно к паре решенных двойственных задач (4.3.1) и (4.3.2) и (3.3) и (3.4) первые два неравенства прямой задачи (4.3.2) превращаются в равенства, откуда следует, что запасы индиго и железного купороса используются полностью. Об этом свидетельствуют и оптимальные значения двойственных переменных: у1=70, у2=90. Напротив, запасы свежегашеной извести используются не полностью, что согласуется со значением третьей двойственной переменной найденного оптимального решения у3=0.
Для целей экономического анализа модели задачи линейного программирования удобно предположить, что двойственные переменные могут выступать в роли оценок типов сырья, используемого в производстве красок. Более того, величина данной двойственной оценки показывает, на сколько возрастет максимальное значение целевой функции прямой задачи при увеличении количества сырья соответствующего типа на 1кг.
|
|
|
Таким образом, двойственные оценки могут быть использованы для определения степени дефицитности типов сырья для производства продукции. В связи с этим анализ оптимальных решений прямой и двойственных задач линейного программирования становится необходимым этапом экономического анализа эффективного планирования производства продукции.
Список литературы
1. Леоненков А. Решение задач оптимизации в среде MS Excel –СПб..БХВ- Петербург, 2005.- 704 с.. ил.
2. Сдвинков О.А. математика в MS Excel 2002- М… Солон-Пресс, 2004-192 с.. ил.
3. Калихман И.Л. Сборник задач по математическому программированию. Изд. 2-е, доп. И перераб. М., “Высшая школа”, 1975.-270 с.
4. Шапкин А.С., Мазаева Н.П. Математичаские методы и модели исследования операций: Учебник.- М.. Издательско-торговая корпорация “Дашков и К°”, 2003.
5. Банди Б. Методы оптимизации. Вводный курс –М.. Радио и связь, 1988.-128 с.
6. Гаас С. Линейное программирование.- М… ГИМФМЛ, 1961-304 с.
7. Гилл Ф., Мюррей У., Райт М. Практическая оптимиация. – М.. Мир, 1985.- 512 с.
8. Заславский Ю.Л. Сборник задач по линейному программированию.- М.. Наука, 1969.- 256.
9. Калихман И.Л. Сборник задач по линейной алгебре и программированию.- М.. Высшая школа, 1969.-160 с.
|
|
|



