 |
Как вычислить двойной интеграл?
|
|
|
|
Понятие двойного интеграла
Двойной интеграл в общем виде записывается следующим образом:

Разбираемся в терминах и обозначениях:
 – значок двойного интеграла;
– значок двойного интеграла;
 – область интегрирования (плоская фигура);
– область интегрирования (плоская фигура);
 – подынтегральная функция двух переменных, часто она довольно простая;
– подынтегральная функция двух переменных, часто она довольно простая;
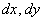 – значки дифференциалов.
– значки дифференциалов.
Что значит вычислить двойной интеграл?
Вычислить двойной интеграл – это значит найти ЧИСЛО. Самое обычное число:

И крайне желательно найти его правильно =)
Результат (число  ) может быть отрицательным. И ноль тоже запросто может получиться. Специально остановился на данном моменте, поскольку немало студентов испытывают беспокойство, когда ответ получается «шото вроде как странный».
) может быть отрицательным. И ноль тоже запросто может получиться. Специально остановился на данном моменте, поскольку немало студентов испытывают беспокойство, когда ответ получается «шото вроде как странный».
Многие помнят, что «обычный» определённый интеграл – тоже число. Здесь всё так же. У двойного интеграла существует и отличный геометрический смысл, но об этом позже, всему своё время.
Как вычислить двойной интеграл?
Для того чтобы вычислить двойной интеграл, его необходимо свести к так называемым повторным интегралам. Сделать это можно двумя способами. Наиболее распространён следующий способ:

Вместо знаков вопроса необходимо расставить пределы интегрирования. Причём одиночные знаки вопроса  у внешнего интеграла – это числа, а двойные знаки вопроса
у внешнего интеграла – это числа, а двойные знаки вопроса  у внутреннего интеграла – это функции одной переменной
у внутреннего интеграла – это функции одной переменной  , зависящие от «икс».
, зависящие от «икс».
Откуда взять пределы интегрирования? Они зависят от того, какая в условии задачи дана область  . Область
. Область  представляет собой обычную плоскую фигуру, с которой вы неоднократно сталкивались, например, при вычислении площади плоской фигуры или вычислении объема тела вращения. Очень скоро вы узнаете, как правильно расставлять пределы интегрирования.
представляет собой обычную плоскую фигуру, с которой вы неоднократно сталкивались, например, при вычислении площади плоской фигуры или вычислении объема тела вращения. Очень скоро вы узнаете, как правильно расставлять пределы интегрирования.
|
|
|
После того, как переход к повторным интегралам осуществлён, следуют непосредственно вычисления: сначала берётся внутренний интеграл  , а потом – внешний. Друг за другом. Отсюда и название – повторные интегралы.
, а потом – внешний. Друг за другом. Отсюда и название – повторные интегралы.
Грубо говоря, задача сводится к вычислению двух определённых интегралов. Как видите всё не так сложно и страшно, и если вы совладали с «обыкновенным» определённым интегралом, что мешает разобраться с двумя интегралами?!
Второй способ перехода к повторным интегралам встречается несколько реже:

Что поменялось? Поменялся порядок интегрирования: теперь внутренний интеграл берётся по «икс», а внешний – по «игрек». Пределы интегрирования, обозначенные звёздочками – будут другими! Одиночные звёздочки внешнего интеграла – это числа, а двойные звёздочки внутреннего интеграла – это обратные функции  , зависящие от «игрек».
, зависящие от «игрек».
Какой бы мы ни выбрали способ перехода к повторным интегралам, окончательный ответ обязательно получится один и тот же:

Пожалуйста, запомните это важное свойство, которое можно использовать, в том числе, для проверки решения.
Алгоритм решения двойного интеграла:
Систематизируем информацию: в каком порядке нужно решать рассматриваемую задачу?
1) Необходимо выполнить чертёж. Без чертежа задачу не решить. Точнее, решать-то она решается, но это будет похоже на игру в шахматы вслепую. На чертеже следует изобразить область  , которая представляет собой плоскую фигуру. Чаще всего фигура незамысловата и ограничена какими-нибудь прямыми, параболами, гиперболами и т.д. Грамотную и быструю технику построения чертежей можно освоить на уроках Графики и основные свойства элементарных функций, Геометрические преобразования графиков. Итак, этап первый – выполнить чертёж.
, которая представляет собой плоскую фигуру. Чаще всего фигура незамысловата и ограничена какими-нибудь прямыми, параболами, гиперболами и т.д. Грамотную и быструю технику построения чертежей можно освоить на уроках Графики и основные свойства элементарных функций, Геометрические преобразования графиков. Итак, этап первый – выполнить чертёж.
2) Расставить пределы интегрирования и перейти к повторным интегралам.
|
|
|
3) Взять внутренний интеграл
4) Взять внешний интеграл и получить ответ (число).
Область интегрирования. Порядок обхода области интегрирования.
Как изменить порядок обхода?
В данном параграфе мы рассмотрим важнейший вопрос – как перейти к повторным интегралам и правильно расставить пределы интегрирования. Как было сказано выше, сделать это можно так:

И так:

На практике эта вроде бы несложная задача вызывает наибольшие затруднения, и студенты часто путаются в расстановке пределов интегрирования. Рассмотрим конкретный пример:
Пример 1
Дан двойной интеграл  с областью интегрирования
с областью интегрирования  . Перейти к повторным интегралам и расставить пределы интегрирования двумя способами.
. Перейти к повторным интегралам и расставить пределы интегрирования двумя способами.
Решение: Изобразим область интегрирования на чертеже:

Обычная плоская фигура и ничего особенного.
Теперь я выдам каждому из вас орудие труда – палку-копалку лазерную указку. Задача состоит в том, чтобы просканировать лучом лазера каждую точку заштрихованной области:

Луч лазера проходит область интегрирования строго снизу вверх, то есть указку вы ВСЕГДА держите ниже плоской фигуры. Луч входит в область через ось абсцисс, которая задаётся уравнением  и выходит из области через параболу
и выходит из области через параболу  (красная стрелка). Чтобы просветить всю область, вам нужно строго слева направо провести указкой вдоль оси
(красная стрелка). Чтобы просветить всю область, вам нужно строго слева направо провести указкой вдоль оси  от 0 до 1 (зелёная стрелка).
от 0 до 1 (зелёная стрелка).
Итак, что получилось:
«игрек» изменяется от 0 до  ;
;
«икс» изменяется от 0 до 1.
В задачах вышесказанное записывают в виде неравенств:

Данные неравенства называют порядком обхода области интегрирования или просто порядком интегрирования
После того, как мы разобрались с порядком обхода, можно перейти от двойного интеграла к повторным интегралам:

Половина задачи решена. Теперь необходимо перейти к повторным интегралам вторым способом. Для этого следует найти обратные функции. Кто ознакомился со вторым параграфом урока Объем тела вращения, тому будет легче. Смотрим на функции, которыми задается область  . Если совсем просто, то перейти к обратным функциям, это значит – выразить «иксы» через «игреки». Единственной функцией, где есть и «икс» и «игрек», является
. Если совсем просто, то перейти к обратным функциям, это значит – выразить «иксы» через «игреки». Единственной функцией, где есть и «икс» и «игрек», является  .
.
Если  , то
, то  , причём:
, причём:
обратная функция  задает правую ветку параболы;
задает правую ветку параболы;
обратная функция  задает левую ветку параболы.
задает левую ветку параболы.
|
|
|
Нередко возникают сомнения, вот, к примеру, функция  определяет левую или правую ветвь параболы? Сомнения развеять очень просто: возьмите какую-нибудь точку параболы, например,
определяет левую или правую ветвь параболы? Сомнения развеять очень просто: возьмите какую-нибудь точку параболы, например,  (с правой ветви) и подставьте её координаты в любое уравнение, например, в то же уравнение
(с правой ветви) и подставьте её координаты в любое уравнение, например, в то же уравнение  :
:

Получено верное равенство, значит, функция  определяет именно правую ветвь параболы, а не левую.
определяет именно правую ветвь параболы, а не левую.
Более того, данную проверку (мысленно или на черновике) желательно проводить всегда, после того, как вы перешли к обратным функциям. Времени займет всего ничего, а от ошибки убережёт наверняка!
Обходим область интегрирования вторым способом:

Теперь лазерную указку держим слева от области интегрирования. Луч лазера проходит область строго слева направо. В данном случае он входит в область через ветвь параболы  и выходит из области через прямую, которая задана уравнением
и выходит из области через прямую, которая задана уравнением 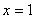 (красная стрелка). Чтобы просканировать лазером всю область, нужно провести указкой вдоль оси
(красная стрелка). Чтобы просканировать лазером всю область, нужно провести указкой вдоль оси  строго снизу вверх от 0 до 1 (зеленая стрелка).
строго снизу вверх от 0 до 1 (зеленая стрелка).
Таким образом:
«икс» изменяется от  до 1;
до 1;
«игрек» изменяется от 0 до 1.
Порядок обхода области следует записать в виде неравенств:

И, следовательно, переход к повторным интегралам таков:

Ответ можно записать следующим образом:

Еще раз напоминаю, что окончательный результат вычислений не зависит от того, какой порядок обхода области мы выбрали (поэтому поставлен знак равенства). Но, до конечного результата ещё далеко, сейчас наша задача – лишь правильно расставить пределы интегрирования.
Пример 2
Дан двойной интеграл  с областью интегрирования
с областью интегрирования  . Перейти к повторным интегралам и расставить пределы интегрирования двумя способами.
. Перейти к повторным интегралам и расставить пределы интегрирования двумя способами.
Это пример для самостоятельного решения. Грамотно постройте чертёж и строго соблюдайте направления обхода (откуда и куда светить лазерной указкой). Примерный образец чистового оформления в конце урока.
Чаще всего типовое задание встречается немного в другой формулировке:
Пример 3
Построить область интегрирования и изменить порядок интегрирования

|
|
|
Решение: По условию дан первый способ обхода области. Решение опять начинается с чертежа. Здесь область  не лежит на блюдечке с голубой каёмочкой, но построить её не составляет особого труда. Сначала «снимаем» функции с пределов интегрирования:
не лежит на блюдечке с голубой каёмочкой, но построить её не составляет особого труда. Сначала «снимаем» функции с пределов интегрирования:  ,
,  . Функция
. Функция  , понятно, задаёт прямую, но что задаёт функция
, понятно, задаёт прямую, но что задаёт функция  ? Давайте её немного преобразуем:
? Давайте её немного преобразуем:
 – окружность с центром в начале координат радиуса 2. Функция же
– окружность с центром в начале координат радиуса 2. Функция же  задаёт верхнюю полуокружность (не забываем, что если есть сомнения, то всегда можно подставить точку лежащую на верхней или нижней полуокружности).
задаёт верхнюю полуокружность (не забываем, что если есть сомнения, то всегда можно подставить точку лежащую на верхней или нижней полуокружности).
Смотрим на пределы внешнего интеграла: «икс» изменяется от –2 до 0.
Выполним чертёж:

Для наглядности я указал стрелками первый способ обхода области, который соответствует повторным интегралам условия:  .
.
Теперь нужно изменить порядок обхода области, для этого перейдем к обратным функциям (выразим «иксы» через «игреки»):

Недавно мы преобразовали функцию  к уравнению окружности
к уравнению окружности  , далее выражаем «икс»:
, далее выражаем «икс»: 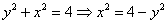
В результате получаем две обратные функции:
 – определяет правую полуокружность;
– определяет правую полуокружность;
 – определяет левую полуокружность.
– определяет левую полуокружность.
Опять же, если возникают сомнения, возьмите любую точку окружности и выясните, где лево, а где право.
Изменим порядок обхода области:

Согласно второму способу обхода, лазерный луч входит в область слева через левую полуокружность  и выходит справа через прямую
и выходит справа через прямую  (красная стрелка). В то же время лазерная указка проводится вдоль оси ординат снизу вверх от 0 до 2 (зелёная стрелка).
(красная стрелка). В то же время лазерная указка проводится вдоль оси ординат снизу вверх от 0 до 2 (зелёная стрелка).
Таким образом, порядок обхода области:

В общем-то, можно записать ответ:

Пример 4
Построить область интегрирования и изменить порядок интегрирования
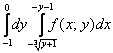
Это пример для самостоятельного решения. Пример не очень сложный, но обратите внимание, что порядок обхода изначально задан вторым способом! Что делать в подобных случаях? Во-первых, возникает трудность с чертежом, поскольку чертить график обратной функции наподобие  непривычно даже мне самому. Я рекомендую следующий порядок действий: сначала из
непривычно даже мне самому. Я рекомендую следующий порядок действий: сначала из  получаем «обычную» функцию (выражаем «игрек» через «икс»). Далее строим график этой «обычной» функции (всегда можно построить хотя бы поточечно). Аналогично поступаем с более простой линейной функцией: из
получаем «обычную» функцию (выражаем «игрек» через «икс»). Далее строим график этой «обычной» функции (всегда можно построить хотя бы поточечно). Аналогично поступаем с более простой линейной функцией: из 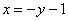 выражаем «игрек» и проводим прямую.
выражаем «игрек» и проводим прямую.
Анализируем исходные пределы интегрирования: входим слева в область через  и выходим через
и выходим через 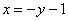 . При этом все дела происходят в «игрековой» полосе от –1 до 0. После того, как вы определили на чертеже область интегрирования, сменить порядок обхода не составит особого труда. Примерный образец оформления решения в конце урока.
. При этом все дела происходят в «игрековой» полосе от –1 до 0. После того, как вы определили на чертеже область интегрирования, сменить порядок обхода не составит особого труда. Примерный образец оформления решения в конце урока.
Похожий пример я еще разберу подробнее чуть позже.
|
|
|
Даже если вы всё отлично поняли, пожалуйста, не торопитесь переходить непосредственно к вычислениям двойного интеграла. Порядок обхода – вещь коварная, и очень важно немного набить руку на данной задаче, тем более, я еще не всё рассмотрел!
В предыдущих четырёх примерах область интегрирования находилась целиком в 1-й, 2-й, 3-й и 4-й координатных четвертях. Всегда ли это так? Нет, естественно.
Пример 5
Изменить порядок интегрирования

Решение: Выполним чертёж, при этом, график функции  фактически представляет собой кубическую параболу, просто она «лежит на боку»:
фактически представляет собой кубическую параболу, просто она «лежит на боку»:

Порядок обхода области, который соответствует повторным интегралам  , обозначен стрелками. Обратите внимание, что в ходе выполнения чертежа прорисовалась еще одна ограниченная фигура (левее оси ординат). Поэтому следует быть внимательным при определении области интегрирования – за область можно ошибочно принять не ту фигуру.
, обозначен стрелками. Обратите внимание, что в ходе выполнения чертежа прорисовалась еще одна ограниченная фигура (левее оси ординат). Поэтому следует быть внимательным при определении области интегрирования – за область можно ошибочно принять не ту фигуру.
Перейдем к обратным функциям:
 – нужная нам правая ветвь параболы;
– нужная нам правая ветвь параболы;
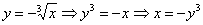
Изменим порядок обхода области. Как вы помните, при втором способе обхода, область нужно сканировать лазерным лучом слева направо. Но тут наблюдается интересная вещь:

Как поступать в подобных случаях? В таких случаях следует разделить область интегрирования на две части и для каждой из частей составить свои повторные интегралы:
1) Если «игрек» изменяется от –1 до 0 (зеленая стрелка), то луч входит в область через кубическую параболу  и выходит через прямую
и выходит через прямую  (красная стрелка). Поэтому порядок обхода области будет следующим:
(красная стрелка). Поэтому порядок обхода области будет следующим:
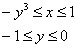
И соответствующие повторные интегралы:

2) Если «игрек» изменяется от 0 до 1 (коричневая стрелка), то луч входит в область через ветвь параболы  и выходит через ту же прямую
и выходит через ту же прямую  (малиновая стрелка). Следовательно, порядок обхода области будет следующим:
(малиновая стрелка). Следовательно, порядок обхода области будет следующим:

И соответствующие повторные интегралы:

У определенных и кратных интегралов есть весьма удобное свойство аддитивности, то есть, их можно сложить, что в данном случае и следует сделать:
 – а вот и наш обход области вторым способом в виде суммы двух интегралов.
– а вот и наш обход области вторым способом в виде суммы двух интегралов.
Ответ записываем так:

Какой порядок обхода выгоднее? Конечно тот, который был дан в условии задачи – вычислений будет в два раза меньше!
Пример 6
Изменить порядок интегрирования

Это пример для самостоятельного решения. В нём присутствуют полуокружности, разборки с которыми были подробно рассмотрены в Примере 3. Примерный образец оформления решения в конце урока.
А сейчас обещанная задача, когда изначально задан второй способ обхода области:
Пример 7
Изменить порядок интегрирования

Решение: Когда порядок обхода задан вторым способом, то перед построением чертежа целесообразно перейти к «обычным» функциям. В данном примере присутствуют два пациента для преобразования:  и
и  .
.
С линейной функцией всё просто: 
График функции  представляется собой параболу с претензией на каноничность.
представляется собой параболу с претензией на каноничность.
Выразим «игрек» через «икс»:

Получаем две ветви параболы:  и
и  . Какую из них выбрать? Проще всего сразу выполнить чертёж. И даже если вы крепко позабыли материал аналитической геометрии о параболе, то всё равно обе ветви можно построить поточечно:
. Какую из них выбрать? Проще всего сразу выполнить чертёж. И даже если вы крепко позабыли материал аналитической геометрии о параболе, то всё равно обе ветви можно построить поточечно:

Еще раз обращаю внимание на тот факт, что на данном чертеже получилось несколько плоских фигур, и очень важно выбрать нужную фигуру! В выборе искомой фигуры как раз помогут пределы интегрирования исходных интегралов:
 , при этом не забывайте, что обратная функция
, при этом не забывайте, что обратная функция  задаёт всю параболу.
задаёт всю параболу.
Стрелочки, которыми обозначен обход фигуры, в точности соответствуют пределам интегрирования интегралов  .
.
Довольно быстро вы научитесь проводить такой анализ мысленно и находить нужную область интегрирования.
Когда фигура найдена, заключительная часть решения, в общем-то, очень проста, меняем порядок обхода области:

Обратные функции уже найдены, и требуемый порядок обхода области:

Ответ: 
Заключительный пример параграфа для самостоятельного решения:
Пример 8
Изменить порядок интегрирования

Полное решение и ответ в конце урока.
|
|
|


