3. Лабораторное задание. 5. Контрольные вопросы. Лабораторная работа № 2. 1. Цель работы. 2. Краткие теоретические сведения

3. Лабораторное задание

3. 1. Используя криптографические алгоритмы замены, составить программу для шифрования и дешифрования текстов.

3. 2. Проверить стойкость шифров, подсчитав статистику для каждого символа текста. Сравнить результаты со стандартной статистической таблицей.

4. Содержание отчета:

· название и цель лабораторной работы;

· описание алгоритма и блок-схемы программы;

· результаты выполнения программы: исходный, зашифрованный и дешифрованный тексты;

· расчеты статистических характеристик;

· выводы, отражающие достоинства и недостатки исследуемых алгоритмов.

 

5. Контрольные вопросы

1. Что называют шифрами замены?

2. Каков общий алгоритм шифров замены?

3. К какому классу относится древний шифр императора Цезаря, как он реализуется, разновидностью какого алгоритма является?

4. Описать разновидности шифра Виженера.

5. Каковы особенности шифра Плейфера?

6. Что является ключом шифра замены? Чему равен ключ составных шифров замены?

7. В чем слабость шифров замены?

8. Как можно увеличить стойкость шифра замены?

 

Лабораторная работа № 2

Шифрование, дешифрование информации с применением криптографических алгоритмов перестановок

1. Цель работы

Криптоанализ и программная реализация алгоритмов перестановок для шифрования и дешифрования исходного текста.

2. Краткие теоретические сведения

Шифры перестановки

Шифр, преобразования из которого изменяют только порядок следования символов исходного текста, но не изменяют их самих, называется шифром перестановки (ШП).

Пусть имеем сообщение из n символов. Его можно представить с помощью таблицы:

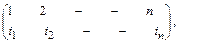
где i₁ - номер места зашифрованного текста, на которое попадает I-ая буква исходного сообщения при выбранном преобразовании, i₂ - номер места для II-й буквы и т. д. В верхней строке таблицы выписаны по порядку числа от 1 до n, а в нижней - те же числа, но в произвольном порядке. Такая таблица называется подстановкой степени n.

Зная подстановку, задающую преобразование, можно как зашифровать, так и расшифровать текст.

Например, если для преобразования используется подстановка:

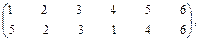
и в соответствии с ней зашифровывается слово МОСКВА, то получится слово КОСМВА.

Итак, используя метод математической индукции, определим, что существует n! вариантов заполнения нижней строки таблицы. Т. е. число различных преобразований шифра перестановки, предназначенного для зашифрования сообщения длины n, меньше либо равно n! . При больших n для вычисления n! можно пользоваться формулой Стирлинга:

.

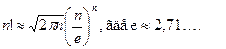 Примером ШП, предназначенного для зашифрования сообщения длины n, является шифр, в котором в качестве множества ключей взято множество всех подстановок степени n. Число ключей такого шифра =n! .

Для использования на практике такой шифр не удобен, т. к. при больших значениях n приходится работать с длинными таблицами.

Примеры простейших шифров перестановок

Широкое распространение получили шифры перестановки, использующие некоторую геометрическую фигуру. Преобразования из этого шифра состоят в том, что в фигуру исходный текст вписывается по ходу одного «маршрута», а затем по ходу другого выписывается из нее. Такой шифр называют маршрутной перестановкой. Например, можно вписывать исходное сообщение в прямоугольную таблицу, выбрав такой маршрут по горизонтали, начиная с левого верхнего угла поочередно слева направо и справа налево. Используем прямоугольник размера 4× 7

è

П	Р	И	М	Е	Р	М	ê
Н	Т	У	Р	Ш	Р	А	ç
О	Й	П	Е	Р	Е	С	ê
И	К	В	О	Н	А	Т	ç

Выписывать будем по вертикали, начиная с верхнего правого угла и двигаясь поочередно сверху вниз и снизу вверх.

МАСТАЕРРЕШРНОЕРМИУПВКЙТРПНОИ

Теоретически, маршруты могут быть более изощренными.

Шифр «Сцитала» эквивалентен следующему шифру маршрутной перестановки: в таблицу, состоящую из m столбцов, построчно записывается сообщение, после чего выписывают буквы по столбцам. Число задействованных столбцов таблицы не может превосходить длины сообщения.

Из истории имеются еще чисто физические ограничения, накладываемые реализацией шифра Сцитала. Естественно предположить, что диаметр жезла не должен превосходить 10 сантиметров. При высоте строки в 1 см на одном витке такого жезла уместится не более 32 букв (10π < 32). Таким образом, число перестановок, реализуемых Сциталой, не больше 32.

Шифр вертикальной перестановки (ШВП). В нем снова используется прямоугольник, в который сообщение вписывается обычным способом (по строкам слева направо). Выписываются буквы по вертикали, а столбцы при этом берутся в порядке, определяемом ключом. Впишем сообщение в прямоугольник, столбцы которого пронумерованы в соответствии с ключом:

В	О	Т	П	Р	И	М
Е	Р	Ш	И	Ф	Р	А
В	Е	Р	Т	И	К	А
Л	Ь	Н	О	Й	П	Е
Р	Е	С	Т	А	Н	О
В	К	И	-	-	-	-

Выбирая столбцы в порядке, заданном ключом, выписываем последовательно буквы сверху вниз:

ОРЕЬЕКРФИЙА-МААЕО-ТШРНСИВЕВЛРВИРКПН-ПИТОТ-

Число ключей ШВП не более m!, где m - число столбцов таблицы. Пользуясь формулой Стирлинга, при больших m и n можно оценить, во сколько раз n! больше m!, если n кратно m.

В случае, когда ключ не рекомендуется записывать, его можно извлекать из какого-то легко запоминающегося слова или предложения.

Например, пусть ключевым словом будет ПЕРЕСТАНОВКА. Буква А получает номер 1. Если какая-то буква входит несколько раз, то ее появления нумеруются последовательно слева направо. Таким образом, второе вхождение А получает номер 2. Поскольку Б нет, то В получает номер 3 и т. д., пока все буквы не получат номера:

ПП	ЕЕ	РР	ЕЕ	СС	ТТ	АА	НН	ОО	ВВ	КК	АА
(9

Транспозиция с фиксированным периодом d. В этом случае сообщение делится на группы символов длины d и к каждой группе применяется одна и та же перестановка. Эта перестановка является ключом; она может быть задана некоторой перестановкой первых d целых чисел. Таким образом, для d=5 в качестве перестановки можно взять: 23154. Это будет означать, что:

 

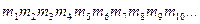
переходит в:

.

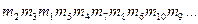Последовательное применение двух или более транспозиций будет называться составной транспозицией. Если периоды этих транспозиций d₁,..., d_s, то, очевидно, в результате получится транспозиция периода d, где d - наименьшее общее кратное d₁,..., d_s.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: