 |
Датчики М-последовательностей
|
|
|
|
М-последовательности также популярны, благодаря относительной легкости их реализации.
М-последовательности представляют собой линейные рекуррентные последовательности максимального периода, формируемые k-разрядными генераторами на основе регистров сдвига. На каждом такте поступивший бит сдвигает k предыдущих и к нему добавляется их сумма по модулю 2. Вытесняемый бит добавляется к гамме.
Строго это можно представить в виде следующих отношений:
r1: =r0 r2: =r1. .. rk-1: =rk-2
r0: =a0 r1 Å a1 r2 Å... Å ak-2 rk-1
Гi: = rk-1-
Здесь r0 r1. .. rk-1 - k однобитных регистров, a0 a1. .. ak-1 - коэффициенты неприводимого двоичного полинома степени k-1. Гi - i-е значение выходной гаммы.
Период М-последовательности исходя из ее свойств равен 2k-1.
Другим важным свойством М-последовательности является объем ансамбля, т. е. количество различных М-последовательностей для заданного k. Эта характеристика приведена в таблице 3. 1.
Таблица 3. 1
| k | Объем ансамбля |
Очевидно, что такие объемы ансамблей последовательности неприемлемы.
Поэтому на практике часто используют последовательности Голда, образующиеся суммированием нескольких М-последовательностей. Объемы ансамблей этих последовательностей на несколько порядков превосходят объемы ансамблей порождающих М-последовательностей. Так при k=10 ансамбль увеличивается от 1023 (М-последовательности) до 388000.
Также перспективными представляются нелинейные датчики ПСП (например сдвиговые регистры с элементом “И” в цепи обратной связи), однако их свойства еще недостаточно изучены.
Возможны и другие, более сложные варианты выбора порождающих чисел для гаммы шифра.
|
|
|
Шифрование с помощью датчика ПСЧ является довольно распространенным криптографическим методом. Во многом качество шифра, построенного на основе датчика ПСЧ, определяется не только и не столько характеристиками датчика, сколько алгоритмом получения гаммы. Один из фундаментальных принципов криптологической практики гласит о том, что даже сложные шифры могут быть очень чувствительны к простым воздействиям.
Шифр Вернама – шифр, в котором открытый текст записан в двоичном виде (последовательность 0; 1), ключ - случайная равновероятная двоичная последовательность той же длины, что и открытый ключ, шифрованный текст получается суммированием по модулю 2 (т. е. 0+0=1+1=0, 0+1=1+0=1). Процедура расшифрования совпадает с процедурой шифрования.
Внешняя простота этого шифра немедленно привлекла внимание специалистов, которые предприняли немало попыток его дешифрования, ни одна из которых не увенчалась успехом. Теоретическую невозможность дешифрования этого шифра, при условии однократного использования случайной равновероятной гаммы-двоичной последовательности, используемой для шифрования путем суммирования с открытым текстом, доказал в своих работах К. Шеннон в середине 30-ых годов. С этого момента шифр приобрел еще одно название - «Совершенно стойкий шифр».
Парадоксально, но факт, если одну и ту же гамму использовать дважды для разных сообщений, то шифр из совершенно стойкого превращается в «совершенно нестойкий» и допускает дешифрование практически вручную. Кроме того, если ключевая последовательность отличается от случайной равновероятной, то шифр также теряет свойство «совершенной стойкости».
При наличии на руках шифрованного текста
ШИФР = 10011000100010001001010010010000
используя для расшифрования ключ
00010010000000110000101000000111
мы получим открытый текст
КЛЮЧ = 1000 1010 1000 1011 1001 1110 1001 0111
|
|
|
используя для расшифрования ключ
00010111000011010001100100001100
мы получим открытый текст
ПЕНЬ = 10001111100001011000110110011100
При этом мы не сможем определить, какой же именно открытый текст был зашифрован, более того, опробуя все ключи, мы получим вообще все возможные открытые тексты, выбрать из которого истинный не сможем в силу отсутствия какого либо критерия выбора.
При всех достоинствах - простота реализации, теоретически гарантированная стойкость, удобство применения этот шифр обладает двумя недостатками - первый и наиболее существенный заключается в том, что объем ключевого материала совпадает с объемом передаваемых сообщений. Второй - с тем, что необходимо иметь эффективные процедуры для выработки случайных равновероятных двоичных последовательностей и специальную службу для развоза огромного количества ключей. Тем не менее, подобные системы шифрования используются на особо важных направлениях секретной связи, например, на некоторых «горячих линиях», их использование обусловлено тем, что шифр имеет теоретически обоснованную стойкость, а на финансирование снабжения ключевой информацией, при защите особо важных каналов денег не считают (что, кстати, вполне резонно).
В связи с вышеизложенным желанием разработчиков систем шифрования стало создание шифров с одной стороны по своим качествам близким к шифру Вернама, с другой стороны не требующих такого объема ключей и сохраняющих стойкость при многократном использовании ключа.
Наиболее близкими по своим качествам к шифру Вернамаявляются шифры гаммирования с псевдослучайной гаммой. Для определения шифра гаммирования в общем виде нам потребуется определение операции модульного сложения и вычитания. Определим ее следующим образом для чисел A и B меньших C и больших или равных нулю.
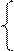
A + B, если (A+B) меньше C
A + B по модулю C =
A + B -C, если (А+ B) больше или равно С,
 |
A - B, если (A-B) больше или равно нулю
A - B по модулю C =
A - B + C, если (А- B) меньше нуля
Например для С=3 эти операции определяются следующим образом
0+0=0 1+0=1 2+0=2
0+1=1 1+1=2 2+1=0
0+2=2 1+2=0 2+2=1
0-0=0 1-0=1 2-0=2
|
|
|
0-1=2 1-1=0 2-1=1
0-2=1 1-2=2 2-2=0
Пусть каждый знак открытого сообщения может принимать С значений (например для русского алфавита без учетов знаков препинания С=33). Занумеруем их от 0 до (С-1).
Шифр гаммирования -шифр, в котором открытый текст, представленный последовательностью чисел, каждое из которых принимает значение от 0 до С-1, преобразуется в шифрованный, представленный аналогичной последовательностью той же длины, путем позначного сложения по модулю C с гаммой - последовательностью чисел, каждое из которых принимает значение от 0 до С-1 длины, равной длине открытого текста и полученной из ключа по какому либо закону.
Пример: используется двоичный ключ длины 3. Первые три знака гаммы совпадают с ключом, каждый следующий знак гаммы равен сумме по модулю 2 трех предыдущих.
Например, в шифре Вернамагамма и ключ суть одно и то же, и операции сложения проводятся по модулю два. Если, при тех же условиях, в качестве ключа использовать некоторую двоичную последовательность фиксированной длины, а двоичную гамму нужной длины вырабатывать из нее по некоторому фиксированному закону, то получается шифр гаммирования псевдослучайной двоичной гаммой. Термин псевдослучайная означает, что ключ выбирается случайно, а сама гамма, лишь внешне похожа на случайную, хотя на самом деле получена по детерминированному закону. Очевидно, что число различных гамм не превышает мощности ключевого множества, и при длине открытых текстов, большей длины ключа шифр гаммирования псевдослучайной гаммой теряет свойство совершенной стойкости. Преимуществом данного шифра является резкое сокращение ключевого материала, необходимого для функционирования сети секретной связи. Для обеспечения стойкости данного шифра необходимо обеспечить два основных условия:
1. Максимальную близость гаммы по статистическим свойствам к случайной равновероятной последовательности независимых величин (далее по аналогии с термином «белый шум», известным из физики, такую последовательность будем называть «белой гаммой»).
2. Отсутствие возможности практического восстановления неизвестных отрезков гаммы (в том числе и ключа) по известным.
|
|
|


