 |
Схемы интегрирования и дифференцирования
|
|
|
|
Схема интегратора может строиться как на основе инвертирующего, так и на основе неинвертирующего усилителя. На рис. 2.16, а показана схема интегратора на основе инвертирующего усилителя.
В цепи обратной связи вместо резистора включается конденсатор. Как известно, конденсатор заряжается током, который на основании двух допущений (см. рис. 2.14, а) равен
.
Как известно из основ электротехники, ток, заряжающий конденсатор, определяется производной от разности напряжений на его обкладках, т.е.
,
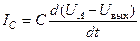а учитывая первое допущение (UA = 0):
.
Приравняв оба выражения для тока IC, получим
.
Интегрируя это выражение, получим
.
Таким образом, выходное напряжение схемы пропорционально интегралу от входного напряжения. Значения сопротивления и емкости определяют постоянный коэффициент схемы интегрирования, что можно объяснить и с чисто физических соображений. Чем больше R и С, тем меньше ток, заряжающий конденсатор, и тем больше величина его емкости, поэтому заряд конденсатора, а следовательно, и выходное напряжение будут нарастать медленнее.
Чтобы иметь схему, обеспечивающую вычисление интеграла с высокой степенью точности, используют усилители с малыми входными токами и дрейфом напряжения смещения нуля, высокоточные резисторы и конденсаторы с малыми токами утечки.
Поменяв местами сопротивление и конденсатор в интеграторе (рис. 2.16, а), получим схему дифференцирования (рис. 2.16, б). Ток конденсатора (с учетом, что UA = 0)
,
а ток в цепи обратной связи по закону Ома
.
Согласно второму допущению эти токи можно считать равными, т.е.
,
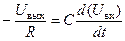откуда
.
Таким образом, выходное напряжение в схеме пропорционально первой производной от входного напряжения.
|
|
|
Рис. 2.16. Схемы интегрирования (а) и дифференцирования (б)
Многие задачи описываются простыми дифференциальными уравнениями. Такие задачи можно решить, реализуя исходное дифференциальное уравнение с помощью аналоговых интегрирующих схем и измеряя установившееся выходное напряжение. Обычное дифференциальное уравнение — это зависимость функции у и ее производных от переменной х. Например, линейное дифференциальное уравнение второго порядка выглядит следующим образом:
.
Для решения уравнения производят замену переменной х на время t, т.е. x = t /τ. Тогда первая и вторая производные 
и 
равны
.
Путем таких преобразований дифференциальное уравнение приводится к виду, которое может быть реализовано на основе схем интегрирования:
,
или
.
Интегрируя левую и правую части уравнения, получим
.
Выражение, стоящее справа, реализуется с помощью интегратора. Обозначим его выходной сигнал переменой z, тогда
.
С использованием переменной z уравнение преобразуется к виду
.
Проинтегрировав обе части уравнения, получим
.
Правая часть этого уравнения, так же как и в предыдущем случае, реализуется с помощью интегратора. Его выходной сигнал соответствует функции – у. Сигнал z поступает с выхода предыдущего интегратора, а сигнал – k 1 y — через обратную связь с собственного выхода.
Рис. 2.17. Аналоговая схема решения дифференциального уравнения
Таким образом, для реализации дифференциального уравнения второго порядка требуется два интегратора и один инвертирующий усилитель (рис. 2.17). Инвертирующий усилитель нужен для изменения знака сигнала с второго интегратора, формирующего – у. Выходной сигнал с этого усилителя с коэффициентом k 0 подается на вход первого интегратора.
|
|
|
