 |
Задания для самостоятельной работы
|
|
|
|
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Юго-Западный государственный университет»
(ЮЗГУ)
Кафедра экономики и управления
«ЭКОНОМИЧЕСКАЯ ОЦЕНКА ИНВЕСТИЦИЙ»
ПРАКТИКУМ
для студентов очной (заочной) формы обучения направления 38.03.03Управление персоналом Профиль «Управление персоналом организации»
Курск 2015
Темы и задания для практических и семинарских занятий
Главная цель практических занятий состоит в том, чтобы студенты на основе прочитанных для них лекций, самостоятельного изучения рекомендуемой литературы, активного участия в обсуждении вопросов на семинарах, дискуссий по актуальным проблемам, выполнения практических заданий овладели современными методами оценки и прогнозирования инвестиционного рынка и отдельных его сегментов; освоили существующие подходы к оценке инвестиционной привлекательности отраслей и регионов; самостоятельно могли принимать решения по выбору эффективных инвестиционных проектов; использовать в управлении предприятием знания о методах инвестиционной деятельности, межфирменной научно-технической кооперации, интеграции науки и частного капитала; управлять временными проблемными коллективами и малыми инновационными фирмами; внедрять новшества в производство.
Темы практических занятий.
Занятие 1
1. Экономическая роль инвестиций, их отличие от капитальных вложений.
2. Законодательная база инвестиционной деятельности РФ.
3. Особенности зарубежного регулирования инвестиционной деятельности.
4. Определение стоимости инвестиционных ресурсов.
|
|
|
Занятие 2.
1. Разделы инвестиционного проекта согласно рекомендациям ЮНИДО.
2. Разработка технико-экономического обоснования (ТЭО) инвестиционного проекта.
Занятие 3.
1. Расчет показателей эффективности инвестиционного проекта.
2. Ранжирование критериев эффективности конкретного инвестиционного проекта.
Занятие 4.
1. Оценка эффективности инвестиций методами, не включающими временной аспект стоимости денег.
Занятие 5.
1. Учет инфляции, неопределенности и риска при принятии решения о реализации инвестиционного проекта.
Занятие 6.
1. Расчет технологической, воспроизводственной и видовой структуры капитальных вложений.
2. Определение сметной стоимости проекта, проектной эффективности капитальных вложений
Занятие 7.
1. Определение эффективности вложения средств в рыночные ценные бумаги.
2. Оценка доходности акций и облигаций.
Занятие 8.
1. Анализ инновационной деятельности предприятия.
2. Разработка основных разделов инновационного проекта.
Задания для практических занятий и пример их выполнения
ЗАДАЧА №1.
Необходимо рассчитать показатели оценки эффективности инвестиционного проекта (NPV, PI, IRR, PP, ARR) на основании данных таблицы 2 и сделать по каждому значению выводы о приемлемости или неприемлемости реализации данного инвестиционного проекта.
Таблица 2
Исходные данные для задачи, тыс. руб.
| Название показателя | 1 год | 2 год | 3 год | 4 год | 5 год |
| 1.Объем реализации | |||||
| 2.Текущие расходы | |||||
| 3.Износ (амортизация) | |||||
| 4.Налогооблагаемая прибыль | |||||
| 5.Налог на прибыль | |||||
| 6.Чистая прибыль | |||||
| 7.Чистые денежные поступления |
R(ставка дисконтирования) = 10%,
I0 (первоначальные инвестиции) = 10000 тыс. руб.
|
|
|
Решение
1. NPV =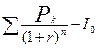 
,
NPV =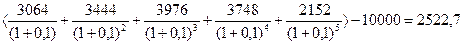 
тыс. руб.
Т.к. NPV > 0, то проект следует принять.
2. PI =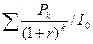 
= 1,25 тыс. руб.
Т.к. PI > 1, то проект следует принять.
3. IRR = r1 +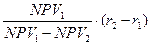 
;
 |
NPV2 = (
) – 10000 = -79,2
IRR = 10000 +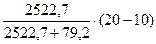 
= 19,6%
Т.к. IRR =19.6%, а предполагаемый WACC=15%, то проект следует принять. (WACC < IRR)
4. PP =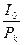 
Т.к. первоначальные инвестиции I0 =10000 руб., то срок окупаемости равен 3 года.
PP = 3064 + 3444 + 3976 =10484 руб.
5. ARR = 
, RV = 5000 руб;
ARR = 
, Þ ARR = 51%.
ЗАДАЧА №2.
Инвестиционная ссуда в размере 50000 руб. выдана на 6 месяцев по простой ставке процентов, равной 28% годовых. Определить наращенную сумму?
Решение:
S = P (1 + n × i), где
S – наращенная сумма;
P – первоначальная сумма;
n – продолжительность периода начисления в годах;
i - относительная величина годовой ставки %.
S = 50 (1 + 0,28 × 0,5) = 57000 руб.
ЗАДАЧА №3.
Инвестиционный кредит в размере 10000 тыс. руб. выдан 2 марта до 11 декабря под 30% годовых (год високосный). Определить размер наращенной суммы для обыкновенного и точного расчета.
Решение:
SS = P (1 + 
× i), где
d – продолжительность периода в днях;
k – продолжительность года в днях.
SS = 10000 (1 + 
× 0,3) = 12366,666;
SS = 10000 (1 + 
× 0,3) = 12327,868.
Разница равна 38798 тыс. руб.
ЗАДАЧА №4.
Кредит в размере 20 млн. руб. выдан на 3,5 года. Ставка % за 1-й год – 30%. За каждое последующее полугодие она снижается на 1%. Определить множитель наращения и наращенную сумму.
Решение:
Определение величины наращенной суммы S называется компаундингом, а определение современной величины P наращенной суммы S называется дисконтированием.
P =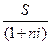 
.
Множитель (коэффициент) наращения – это величина, показывающая, во сколько раз вырос первоначальный капитал.
К-т наращения = 20 (1 + 0,3 + 0,5 × 0,29 + 0,5 × 0,28 + 0,5 × 0,27 + 0,5 × 0,26 + 0,5 × 0,25) = 20 × 1,975 = 39,5 млн. руб.
ЗАДАЧА №5.
Кредит на капитальные вложения на полгода выдается по простой учетной ставке 20%. Необходимо рассчитать сумму, получаемую заемщиком и величину дисконта, если требуется возвратить 30 млн. руб.
Решение:
Дисконт – это доход, полученный по учетной ставке, т.е. разница между размеров кредита и непосредственно выдаваемой суммы.
|
|
|
30 =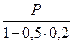 
Þ P = 30 (1 – 0,1) = 27 млн. руб.
Дисконт = 30 – 27 = 3 млн. руб.
ЗАДАЧА №6.
Первоначальная вложенная сумма равна 200 тыс. руб. Определить наращенную сумму через 5 лет при использовании простой и сложной ставок процентов в размере 28% годовых.
Решение:
Сложные проценты начисляются к сумме долга и к начисленным за предыдущие интервалы времени проценты.
S = P (1 + ic)n,
где ic – относительная величина годовой ставки сложных ссудных процентов.
КНС = (1 + ic)n;
P = 
- текущая стоимость.
P = S × a,
где а – коэффициент дисконтирования
a = 
или а = 
.
Таким образом, текущий денежный эквивалент будущей денежной суммы тем ниже, чем отдаленнее срок ее получения и чем выше норма доходности.
Простые %: S = 200 (1 + 5 × 0,28) = 480 тыс. руб.
Сложные %: S = 200 (1 + 0,28)5 = 687,19 тыс. руб.
Формула для определения сложных ставок процентов по полугодиям и кварталам имеет вид:
Smn = P (1 +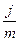 
)mn
По полугодиям: S = 200 (1 + 0,14)10 = 741,44;
По кварталам: S = 200 (1 + 0,07)20 = 773,94.
ЗАДАЧА №7.
Определить современную (текущую, настоящую) приведенную величину суммы в размере 100 млн. руб., выплачиваемой через 3 года, при использовании ставки сложных процентов.
Решение:
P = ;
Р = 
= 52,63.
ЗАДАЧА №8.
Первоначальная сумма долга составляет 50 млн. руб. Определить наращенную сумму через 2,5 года, используя два способа начисления сложных процентов по ставке 25% годовых.
Решение:
1. S = P (1 + ic)n = 50 (1 + 0,25)2,5 = 87,346 млн. руб.
2. S = P (1 + ic)na × (1 + nb × ic)
u = na + nb
u = 2 +0,5
Smn = 50 (1 +0,25)2 × (1 + 0,5 × 0,25) = 87,890 млн. руб.
Задания для самостоятельной работы
| Форма СРС | Наименование раздела дисциплины | Срок выполнения | Время, затрачиваемое на выполнение СРС, час. |
| Р, П | Решение конкретных экономических задач по отдельным вопросам, не предусмотренным практическими занятиями | 20 марта | |
| Р, П | Методы косвенного (экономического) регулирования | 9 апреля | |
| Р, П | Методы прямого (административного) участия государства в инвестиционной деятельности, осуществляемой в виде капитальных вложений | 26 апреля | |
| Р, П | Проектно-сметная документация (организация проектно-сметных работ) | 15 мая | |
| Р, П | Простые (статические) методы оценки эффективности инвестиционных проектов | 27 мая | |
| Р, П | Дисконтированный (динамический) метод оценки эффективности инвестиционных проектов | 5 июня | |
| Итого |
|
|
|
|
|
|
