 |
Точка, принадлежащая поверхности
|
|
|
|
Точка принадлежит поверхности, если она принадлежит линиям, составляющим каркас поверхности, а также любым линиям принадлежащим поверхности.
Рассмотрим построение проекций точек, принадлежащих поверхности конуса (рис.2), когда одна проекция точки задана. Проекция А2принадлежит очерковой образующей, следовательно проекция А1строится переносом по линии связи. На фронтальной проекции основания конуса расположена проекция точки В2, горизонтальных проекций можно построить две, на передней и задней стороне конуса, поэтому рассматриваем конкурирующие точки В и В `. На фронтальной проекции конуса зададим проекцию точкиD2иD2 `. Для того чтобы построить вторые горизонтальные проекции точек необходимо использовать вспомогательные линии: параллель или образующие. Воспользуемся параллелью, для построения горизонтальной проекции параллели, радиусотмеряется всегда от оси вращения до очерковой образующей. Для построения фронтальной проекции точки С использована образующая, которую провели через заданную проекцию. Положение образующей на основании отмечено крестиком.
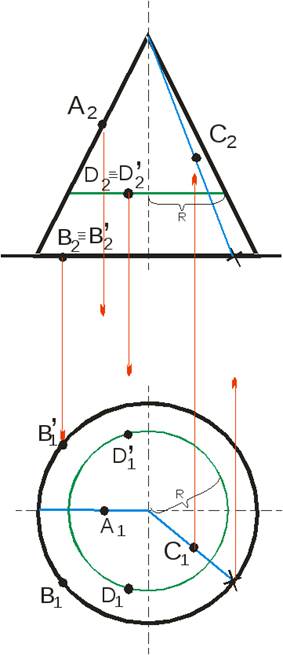
Рисунок 2. Построение точек, принадлежащих поверхности конуса.
Пересечение поверхности плоскостью.
Конические сечения.
В зависимости от положения плоскости по отношению к плоскостям проекций, сложность решения задачи, по определению линии пересечения ее с поверхностью существенно меняется. Наиболее простым представляется случай, когда плоскость проецирующая. Рассмотрим решение задачи по определению линии пересечения конуса фронтально - проецирующей плоскостью (рис.3). На фронтальной плоскости проекций линия пересечения определена, требуется построить ее вторую горизонтальную проекцию.
|
|
|
Линия пересечения плоскости с поверхностью имеет форму кривой, для ее построения определим основные и вспомогательные точки. Основные точки:
- верх и низ кривой;
- принадлежащие очерковым образующим;
- принадлежащие основанию, экватору.
Вспомогательные точки служат для уточнения формы кривой, их следует располагать приблизительно на равном расстоянии между основными.
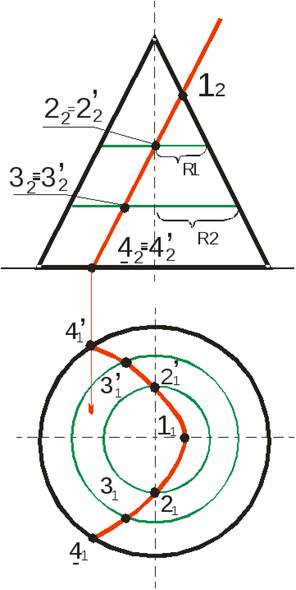
Рисунок 3.Построение линии пересечения конуса
с фронтально-проецирующей плоскостью.
Точки 1 и 4 являются основными точками, их горизонтальные проекции строятся без вспомогательных построений по принципу принадлежности. Точки 2 и 3 – вспомогательные, для их построения использованы параллели. После того как будут построены горизонтальные проекции точек соединим их плавной симметричной относительно горизонтальной оси конуса линией, которая по форме является параболой.
Рассмотрим сечение конуса горизонтально-проецирующей плоскостью (рис.4). На горизонтальной плоскости проекций линия пересечения определена, чтобы построить вторую проекцию этой линии пересечения, обозначим основные (1, 4 и 6) и вспомогательные точки (3, 2). Точки 6 и 1 принадлежат основанию конуса их вторые проекции построить легко. Точка 5 принадлежит очерковой образующей и является границей видимости кривой на фронтальной проекции, ее построение не представляет трудности. Вершина кривой это точка (4), которая находится ближе всего к вершине конуса (в предыдущей задачи она определялась на фронтальной проекции), то есть на перпендикуляре, опущенном из вершины конуса. Точки 3 и 2 являются вспомогательными. Для построения точек 4, 3 и 2 воспользуемся параллелями. Чтобы построить фронтальные проекции параллелей обозначим их пересечение с очерковой образующей крестиками и перенесем их на фронтальную проекцию образующей. После того как будут построены все проекции точек, соединим их плавной линией, при этом участок 6-5 будет невидимым, поэтому его следует провести пунктирной линией. Полученная кривая имеет форму гиперболы.
|
|
|

Рисунок 4. Построение линии пересечения конуса
с горизонтально-проецирующей плоскостью
В зависимости от положения секущей плоскости линиями сечения конической поверхности могут быть (рис.5): эллипс, парабола, гипербола, окружность и треугольник.
Если плоскость Ф пересекает все образующие поверхности конуса вращения, т.е. если φ > α, то линией сечения является эллипс (рис.5). В этом случае секущая плоскость не параллельна ни одной из образующих поверхности конуса.
В случае, когда плоскость перпендикулярна оси вращения конуса, в сечении получается окружность.
Если плоскость Ф параллельна одной образующей поверхности конуса, т.е. φ = α, то линией пересечения является парабола (рис.5). В случае, когда плоскость проходит через вершину конуса, линия пересечения совпадает с образующими. В сечении получается треугольник.
Если секущая плоскость параллельна оси вращения, в сечении – гипербола.
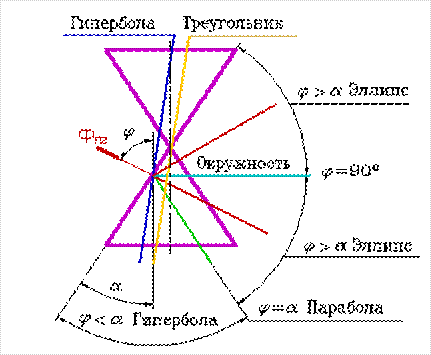
Рисунок 5. Конические сечения.
Развертка конуса.
Если задана поверхность прямого конуса, то развертка его боковой поверхности представляет круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ =360о r / l, где r – радиус окружности основания конуса. Для простоты построения используется аппроксимация длинны окружности основания конуса, для чего конус вписывается в 12-угольную пирамиду (рис.6).

Рисунок 5. Построение развертки конуса.
Построение развертки конуса начинаем с деления основания на 12 частей радиусом. Точки деления обозначаем римскими цифрами. Радиусом, равном очерковой образующей, строим сектор круга. Длина дуги определяется, последовательно откладывая на ней полученные при делении отрезки. Для построение точки С, принадлежащей поверхности конуса, строим на развертке образующую, на которой располагается точка. Чтобы определить натуральную величину расстояния от точки С до вершины конуса, переносим ее на очерковую образующую (метод вращения разбирали при построении развертки пирамиды).
|
|
|


