 |
Следует имеет в виду, что линия пересечения двух поверхностей в проекциях всегда располагается в зоне общей для этих пересекающихся поверхностей
|
|
|
|
Характер линии пересечения кривых поверхностей зависит от формы поверхностей и от из взаимного положения. Линия пересечения имеет форму замкнутой или незамкнутой кривой, за исключением случаев, когда пересекаются два цилиндра, оси вращения которых параллельны, когда пересекаются два конуса вершины которых совпадают. В этих случаях линия пересечения прямая.
Задача на построение линии пересечения значительно упрощается, если одна поверхность занимает проецирующее положение. Для этого целесообразно воспользоваться преобразованием чертежа, чтобы представить пересекающиеся поверхности в частном положении или воспользоваться третьей проекцией.
Например (рис.1), на П3цилиндр занимает проецирующее положение.

Рисунок 1. Построение линии пересечения цилиндра и конуса с
использованием третьей проекции.
Рассмотрим некоторые случаи взаимного расположения поверхностей, которые определяют характер линии пересечения.
1. Поверхности могут полностью или не полностью пересекаться (рис. 2). В случае неполного проникновения (рис.2. а.) линия пересечения – замкнутая или незамкнутая пространственная кривая линия, симметричная очерковой образующей. В случае полного проникновения (рис.2 б.) линия пересечения состоит из двух симметричных частей. На рисунке 2. в) две симметричные части кривой соединяются в точке касания. Проникновение с точкой касания.

а) б) в)
Рисунок 2. Пересечение конуса и цилиндра
а) Неполное проникновение; б) Полное проникновение; в) Проникновение
с точкой касания.
2. Оси поверхностей вращения параллельны:
- находятся в одной меридиональной плоскости (рис.3 а.). Линия пересечения симметрична относительно главного меридиана и совпадает.
|
|
|
- находятся в разных плоскостях (рис.3 б.). Линия пересечения симметрична относительно линии, соединяющей центры поверхностей.

а.) б.)
Рисунок 3. а) Ось конуса и цилиндра находятся в одной меридиональной плоскости, б) Ось конуса и цилиндра находятся в разных плоскостях.
3. Оси поверхностей вращения совпадают. Такие поверхности называются соосными. Линия пересечения таких поверхностей окружность (рис. 4).
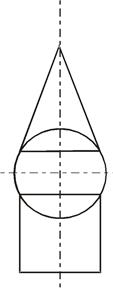
Рисунок 4. Пересечение соосных поверхностей цилиндра, конуса и сферы.
4. Особый случай пересечения поверхностей. Теорема Монжа.Если две поверхности второго порядка описаны около третьей или вписаны в нее, то линия их пересечения распадается на две плоские кривые второго порядка. Плоскости этих кривых проходят через прямую, соединяющую точки линий касания. Рисунок 5.
 а) б)
а) б)
Рисунок 5. Особый случай пересечения поверхностей.
а) Наглядное изображение. б) Эпюр.
Рассмотрим случай пересечения поверхностей вращения, ни одна из которых не является проецирующей. В этом случае линия пересечения строиться на обеих плоскостях проекций (рис. 6).
Построение линии пересечения выполняется в следующем порядке:
1. Анализируем взаимное положение и форму поверхностей.
2. Определяем положение основных и вспомогательных точек методом секущих плоскостей.
3. Соединяем полученные точки.
Разберем подробно второй пункт. Точки верха (1) и точка низа кривой (4) располагаются на пересечении главных меридианов (очерковых образующих) сферы и конуса, так как их оси вращения лежат в одной плоскости, параллельной П2. и через них можно провести вспомогательную секущую плоскость.
Между точками 1 и 4 будут располагаться основные и вспомогательные точки. Проведем вспомогательную секущую плоскость перпендикулярно оси вращения конуса на уровне экватора сферы, для того чтобы определить положение основных точек (3), которые на горизонтальной проекции определят границу видимости, а на фронтальной плоскости проекций они будут совпадать ввиду симметрии линии пересечения.
|
|
|
Данная вспомогательная секущая плоскость II пересекает конус по окружности соответствующего радиуса, сферу также по окружности. Построим эти окружности на горизонтальной плоскости проекций. На пересечении этих окружностей (сечений) получаются горизонтальные проекции искомых точек 3. Теперь необходимо построить их фронтальные проекции, спроецировав на секущую плоскость.
Для уточнения формы кривой воспользуемся вспомогательными точками (2). Для этого проведем вспомогательную секущую I плоскость между точкой 1 и экватором сферы.
Проведение секущей плоскости III нижеточки 4 не имеет смысла, так как в этой плоскости сфера и конус не будут иметь общих точек.
Теперь можно соединить полученные точки с учетом видимости на горизонтальной проекции.

Рисунок 6. Построение линии пересечения конуса и сферы.
|
|
|


