 |
Кинематическое исследование механизма.
|
|
|
|
2.1. Построение планов положений механизма.
Планы 12 положений механизма изображаются на первом листе чертежа курсовой работы. Они нужны для того, чтобы:
а) показать положение всех звеньев механизма в различные моменты времени;
б) определить ход ползуна;
в) определить угол размаха коромысла;
г) показать траекторию движения какой - либо точки. В данном задании – траекторию движения центра масс шатуна 4 (точка S 4).
Построение проводим в масштабе. Под масштабом понимают отношение действительной длины звена в метрах, к длине звена на чертеже в мм, например: 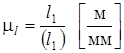 ; длина кривошипа на чертеже должна быть (l 1) = 40¸70 мм.
; длина кривошипа на чертеже должна быть (l 1) = 40¸70 мм.
Принимаем в нашем случае (l 1) = 40 мм. Тогда масштаб длин будет равен
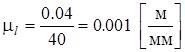
Теперь можно определить все остальные размеры на чертеже по формуле 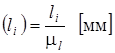
Эти размеры будут равны:
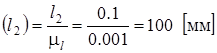
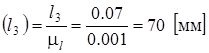
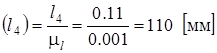
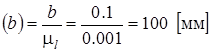
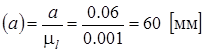
Далее вычерчиваем планы механизма в 12 положениях, используя рассчитанные длины и расстояния. Затем строим предельные положения механизма и определяем ход ползуна НЕ (в метрах) и угол размаха коромысла g (в градусах).
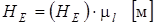
2.2. Построение планов скоростей механизма.
Планы скоростей механизма изображаются на первом листе чертежа. Они нужны для того, чтобы:
а) определить величину и направление скорости любой точки механизма в различные моменты времени;
б) определить угловые скорости звеньев в различные моменты времени.
Построение планов скоростей проводим в соответствии с формулой, известной из теоретической механики:
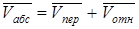 , (1)
, (1)
где: 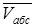 – абсолютная скорость точки;
– абсолютная скорость точки;
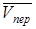 – переносная скорость выбранного полюса;
– переносная скорость выбранного полюса;
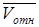 – скорость точки относительно выбранного полюса.
– скорость точки относительно выбранного полюса.
Для того, чтобы начертить планы скоростей, сначала нужно вычислить скорость точки В кривошипа АВ. Эту скорость определяем по формуле
|
|
|
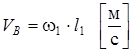 ,
,
где: 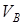 – модуль скорости точки В;
– модуль скорости точки В;
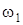 – заданная угловая скорость движения кривошипа,
– заданная угловая скорость движения кривошипа, 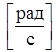 ;
;
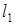 – заданная длина кривошипа (в метрах).
– заданная длина кривошипа (в метрах).
В нашем случае:
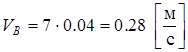
Эту скорость нужно показать на чертеже в виде вектора, перпендикулярного кривошипу АВ и имеющего длину 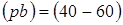 мм. Принимаем
мм. Принимаем 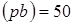 мм. Тогда масштаб будущего плана скоростей
мм. Тогда масштаб будущего плана скоростей 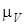 будет равен
будет равен
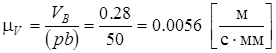
Для определения скорости точки С записываем векторные уравнения вида (1)
|
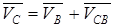
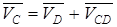
Для определения скорости точки Е записываем аналогичные векторные уравнения
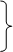
|
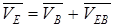
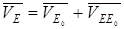
Далее строим планы скоростей для каждого положения механизма, используя в каждом из них вектор 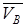 и векторные уравнения (2) и (3). После построения всех 12 планов скоростей определяем величины скоростей всех характерных точек механизма, используя формулу
и векторные уравнения (2) и (3). После построения всех 12 планов скоростей определяем величины скоростей всех характерных точек механизма, используя формулу
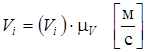 ,
,
где: 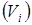 – длина вектора скорости характерной точки на плане скоростей;
– длина вектора скорости характерной точки на плане скоростей;
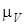 – масштаб плана скоростей, вычисленный ранее.
– масштаб плана скоростей, вычисленный ранее.
Угловые скорости вращательного движения звеньев 2, 3, 4 можно рассчитать по формуле
 ,
,
где: 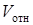 – относительная скорость, полученная из плана скоростей,
– относительная скорость, полученная из плана скоростей, 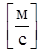 ;
;
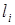 – длина соответствующего звена, [м].
– длина соответствующего звена, [м].
Результаты вычислений 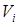 и
и 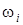 сводим в таблицу 2.
сводим в таблицу 2.
|
| ||||||||||||||
| VB (м/с) | ||||||||||||||
| VE (м/с) | ||||||||||||||
| VC (м/с) | ||||||||||||||
| VCB (м/с) | ||||||||||||||
| VEB (м/с) | ||||||||||||||
| VS 2 (м/с) | ||||||||||||||
| VS 3 (м/с) | ||||||||||||||
| VS 4 (м/с) | ||||||||||||||
| w2 (1/с) | ||||||||||||||
| w3 (1/с) | ||||||||||||||
| w4 (1/с) |
|
|
|
2.3. Построение планов ускорений механизма.
Планы ускорений механизма изображаются на первом листе чертежа. Они нужны для того, чтобы:
а) определить величину и направление ускорения любой точки механизма в различные моменты времени;
б) определить угловые ускорения звеньев в различные моменты времени.
Построение планов ускорений проводим в соответствии с формулами, известными из теоретической механики:
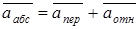 , (4)
, (4)
где:
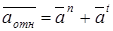 – если относительное движение является вращательным, (5)
– если относительное движение является вращательным, (5)
 – если в относительном движении вращается кулиса, вдоль которой
– если в относительном движении вращается кулиса, вдоль которой
поступательно движется кулисный камень. (6)
В этих формулах:
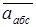 – абсолютное ускорение точки; апер – переносное ускорение точки;
– абсолютное ускорение точки; апер – переносное ускорение точки;
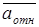 – полное относительное ускорение точки;
– полное относительное ускорение точки;
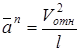 – нормальное относительное ускорение точки; (7)
– нормальное относительное ускорение точки; (7)
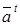 – тангенциальное относительное ускорение точки;
– тангенциальное относительное ускорение точки;
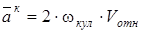 – ускорение Кориолиса; (8)
– ускорение Кориолиса; (8)
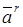 – относительное ускорение кулисного камня вдоль оси кулисы.
– относительное ускорение кулисного камня вдоль оси кулисы.
Для того, чтобы изобразить планы ускорений, сначала нужно вычислить ускорение точки В кривошипа АВ. Это ускорение определяем по формуле
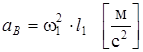 ,
,
где: 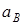 – модуль ускорения точки В кривошипа;
– модуль ускорения точки В кривошипа;
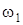 – заданная угловая скорость движения кривошипа,
– заданная угловая скорость движения кривошипа, 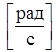 ;
;
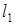 – заданная длина кривошипа (в метрах).
– заданная длина кривошипа (в метрах).
В нашем случае: 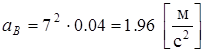
Это ускорение нужно показать на чертеже в виде вектора, параллельного кривошипу АВ и имеющего длину 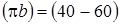 мм. Принимаем
мм. Принимаем 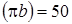 мм. Тогда масштаб будущего плана ускорений
мм. Тогда масштаб будущего плана ускорений 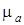 будет равен
будет равен
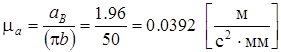
Вычисляем нормальное ускорение точки С в относительном движении вокруг точки В по формуле (7)
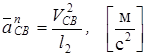
Вычисляем длину отрезка 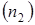 , изображающего это ускорение на чертеже
, изображающего это ускорение на чертеже
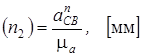
Вычисляем нормальное ускорение точки Е в относительном движении вокруг точки В по формуле (7)
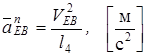
Вычисляем длину отрезка 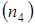 , изображающего это ускорение на чертеже
, изображающего это ускорение на чертеже
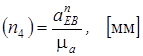 .
.
Аналогичные операции производим для всех 12 положений механизма, результаты заносим в таблицу 3.
Таблица 3. Численные значения и длины отрезков нормальных ускорений точек.
|
|
|
| Полож. мех. | ||||||||||||

| ||||||||||||
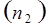
| ||||||||||||
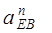
| ||||||||||||
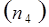
|
Далее строим планы ускорений для 12 положений механизма в соответствии с векторными уравнениями (4)÷(6), используя данные таблицы 3.
После их построения определяем величины ускорений всех характерных точек механизма (абсолютные и относительные) по формуле
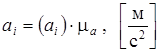 ,
,
где:  – действительное ускорение данной точки (абсолютное или относительное),
– действительное ускорение данной точки (абсолютное или относительное),
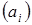 – длина вектора ускорения данной точки на плане ускорений, [мм].
– длина вектора ускорения данной точки на плане ускорений, [мм].
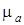 – масштаб плана ускорений.
– масштаб плана ускорений.
Угловые ускорения звеньев 2, 3, 4 можно рассчитать по формуле
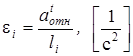 ,
,
где: 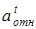 – относительное ускорение, полученное из плана ускорений,
– относительное ускорение, полученное из плана ускорений, 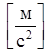 ;
;
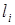 – длина соответствующего звена, [м].
– длина соответствующего звена, [м].
Результаты вычислений ускорений точек  и угловых ускорений звеньев
и угловых ускорений звеньев  заносим в сводную таблицу 4.
заносим в сводную таблицу 4.
Таблица 4. Значения ускорений точек и угловых ускорений звеньев механизма.
| aB | ||||||||||||
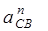
| ||||||||||||
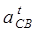
| ||||||||||||
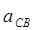
| ||||||||||||
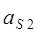
| ||||||||||||
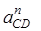
| ||||||||||||
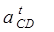
| ||||||||||||
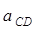
| ||||||||||||
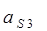
| ||||||||||||
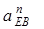
| ||||||||||||
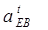
| ||||||||||||
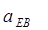
| ||||||||||||
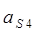
| ||||||||||||
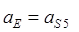
| ||||||||||||
| e2 | ||||||||||||
| e3 | ||||||||||||
| e4 |
|
|
|
2.4. Построение диаграмм перемещений, скоростей и ускорений ползуна.
Кинематические диаграммы – это графическое изображение перемещений, скоростей и ускорений отдельных точек механизма как функций времени или угла поворота кривошипа:
S = S(t), V = V(t), а = а (t),
или S = S (j), V = V (j), а = а (j).
Если построены планы 12 положений механизма, то можно построить кривую перемещения в зависимости от времени S(t), а затем, используя приёмы графического дифференцирования, построить кривые скорости V(t) и ускорения а(t).
Порядок построения кинематических диаграмм:
1. Проводим оси кинематических диаграмм.
2. Откладываем на оси времени отрезок l = (150÷200) мм, соответствующий времени одного полного оборота кривошипа. Принимаем l = 180 мм. При этом масштаб времени будет равен
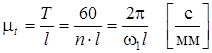
3. Масштаб перемещений m s принимаем равным или кратным масштабу m l плана положений механизма.
4. Строим диаграмму перемещений ползуна S = S (j), используя планы положений механизма.
5. Для того чтобы отрезки на оси ординат диаграммы скоростей были равны отрезкам на планах скоростей, построенных ранее, необходимо найти полюсное расстояние HV. Вычисляем его по формуле
 [мм],
[мм],
где: 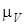 – масштаб планов скоростей, построенных ранее.
– масштаб планов скоростей, построенных ранее.
6. Строим диаграмму скоростей ползуна V = V (j), используя приёмы графического дифференцирования (метод хорд).
7. Вычисляем полюсное расстояние Ha по аналогичной формуле
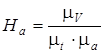 [мм],
[мм],
где: 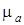 – масштаб планов ускорений, построенных ранее.
– масштаб планов ускорений, построенных ранее.
8. С помощью построенной диаграммы скоростей V = V (j) строим диаграмму ускорений а = а (j), используя тот же метод хорд.
Силовой расчёт механизма.
3.1. Определение силы сопротивления Рс по индикаторной диаграмме.
Изображаем механизм в положении, заданном для силового расчёта (см. лист 2). Отсоединяем от механизма группу Ассура, состоящую из звеньев 4 и 5 и вычисляем по индикаторной диаграмме силу РС, действующую на ползун. Для этого:
1. Строим индикаторную диаграмму под схемой механизма так, чтобы по оси абсцисс величина HС на индикаторной диаграмме совпадала с полным ходом ползуна HС на схеме механизма, а по оси ординат диаграммы изображалась сила Рmах, действующее на ползун, в масштабе 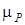 равном
равном
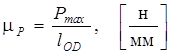 ,
,
где 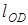 - длина отрезка ОD в мм.
- длина отрезка ОD в мм.
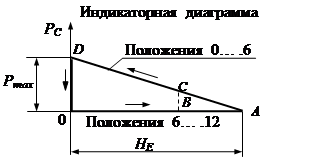 | |||||
|
|
|
2. Определяем на индикаторной диаграмме абсциссу ОВ, соответствующую положению механиза, указанному в задании для силового расчёта.
3. Ордината СВ (мм), соответствует силе сопротивления РС.
4. Вычисляем величину силы сопротивления по формуле
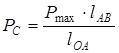 .
.
Определяем силы тяжести звеньев по формуле 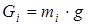 . Результаты сводим в таблицу 5.
. Результаты сводим в таблицу 5.
Таблица 5. Значения силы тяжести звеньев механизма
| Номер звена | ||||
| Масса звена (кг) | т 2 = | т 3 = | т 4 = | т 5 = |
| Сила тяжести (Н) | G 2 = | G 3 = | G 4 = | G 5 = |
Определяем силы инерции и моменты инерционных сил звеньев в положении, заданном для силового расчёта. Согласно принципу Даламбера:
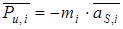
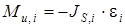
Результаты вычислений сводим в таблицу 6.
Таблица 6. Значения масс, сил инерции и моментов сил инерции звеньев.
| Номер звена | ||||
| Масса звена (кг) | т 2 = | т 3 = | т 4 = | т 5 = |
| Сила инерции (н) | Ри ,2 = | Ри ,3 = | Ри ,4 = | Ри ,5 = |
| Момент инерции звена (кг.м2 ) | JS 2 = | JS 3 = | JS 4 = | |
| Момент инерци- онных сил (н.м ) | Ми ,2 = | Ми ,3 = | Ми ,4 = |
Переносим с листа №1 на лист №2 план ускорений в положении, заданном для силового расчёта.
Показываем все силы и моменты на плане механизма. В центрах масс звеньев (точки S 2 , S 3 , S 4 , S 5) вертикально вниз – силы тяжести. В этих же точках показываем силы инерции, направленные в сторону, противоположную вектору ускорения данного центра масс.
Силу сопротивления прикладываем к ползуну и направляем так, как показано на схеме задания.
Моменты инерционных сил направляем противоположно угловым ускорениям звеньев e2, e3, e4.
3.2. Силовой расчёт группы Ассура 2-го класса 2-го вида.
Отсоединяем от механизма группу Ассура, состоящую из звеньев 4 и 5. Заменяем действие 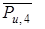 и
и  действием одной силы
действием одной силы 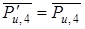 , но приложенной не в центре масс, а в точке Т 4 (точке качания звена), положение которой определяем после нахождения плеча h 4, равного
, но приложенной не в центре масс, а в точке Т 4 (точке качания звена), положение которой определяем после нахождения плеча h 4, равного
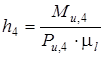 [мм].
[мм].
Переносим силу 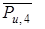 параллельно самой себе в точку Т 4.
параллельно самой себе в точку Т 4.
Определяем реакции в кинематических парах.
Прикладываем к звеньям рассматриваемой группы все внешние силы, действующие на неё: 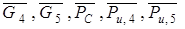 . Действие отброшенных звеньев (кривошипа 1 и стойки 0) заменяем реакциями
. Действие отброшенных звеньев (кривошипа 1 и стойки 0) заменяем реакциями 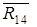 и
и 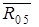 . Реакцию
. Реакцию 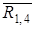 разложим на 2 составляющие:
разложим на 2 составляющие:
 , направленную по оси звена 4;
, направленную по оси звена 4;
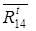 , направленную перпендикулярно оси звена 4.
, направленную перпендикулярно оси звена 4.
Реакция 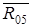 перпендикулярна направлению движения ползуна.
перпендикулярна направлению движения ползуна.
При определении реакций в кинематических парах используем уравнения равновесия всей структурной группы или её звеньев, представленных в виде:
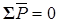 , (1)
, (1)
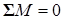 . (2)
. (2)
Составим уравнение вида (2) для звена 4:
 , то есть
, то есть 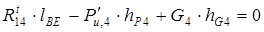 ,
,
откуда 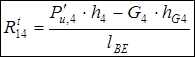 (н),
(н),
где 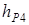 и
и 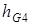 находим по чертежу:
находим по чертежу: 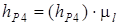 ;
; 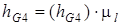
Составляем уравнение (1) для структурной группы второго вида (звеньев 4 и 5):
 , т.е.
, т.е. 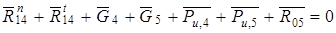 (3)
(3)
Строим план сил группы согласно уравнению (3) в выбранном масштабе 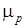 .
.
В результате построения плана сил находим величины 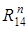 и
и 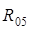 по формулам:
по формулам:
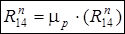 (н);
(н); 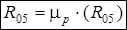 (н).
(н).
Полная реакция звена 1 на звено 4 равна геометрической сумме
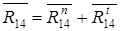 ;
;  (н).
(н).
Для нахождения реакции 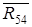 напишем уравнение вида (1) для звена 4.
напишем уравнение вида (1) для звена 4.
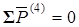 ;
; 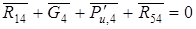 (4)
(4)
Строим план сил звена 4, из которого находим величину 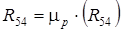 (н).
(н).
Для определения точки приложения силы 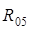 составим уравнение равновесия вида (2) для звена 5:
составим уравнение равновесия вида (2) для звена 5:
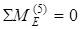 ;
; 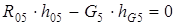 , из этого выражения находим
, из этого выражения находим
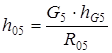 (5)
(5)
Поскольку по условию центр масс звена 5 совпадает с точкой Е, то 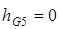 .
.
Из выражения (5) следует, что 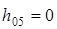 , то есть реакция
, то есть реакция 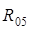 приложена в точке Е.
приложена в точке Е.
3.3. Силовой расчёт группы Ассура 2-го класса 1-го вида.
Отсоединяем от механизма группу Ассура, состоящую из звеньев 2 и 3. Заменяем действие 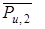 и
и 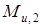 действием одной силы
действием одной силы 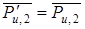 , но приложенной не в центре масс, а в точке Т 2, положение которой определяем после нахождения плеча h 2:
, но приложенной не в центре масс, а в точке Т 2, положение которой определяем после нахождения плеча h 2: 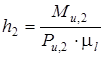 [мм].
[мм].
Переносим силу 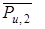 параллельно самой себе в точку Т 2.
параллельно самой себе в точку Т 2.
Аналогичные действия производим со звеном 3.
Заменяем действие 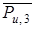 и
и 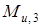 действием одной силы
действием одной силы 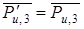 , но приложенной не в центре масс, а в точке Т 3, положение которой определяем после нахождения плеча h 3, равного
, но приложенной не в центре масс, а в точке Т 3, положение которой определяем после нахождения плеча h 3, равного 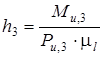 [мм].
[мм].
Переносим силу 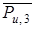 параллельно самой себе в точку Т 3.
параллельно самой себе в точку Т 3.
Определяем реакции в кинематических парах.
Прикладываем к звеньям рассматриваемой группы все внешние силы, действующие на неё:  . Действие звена 1 и стойки 0 заменяем реакциями
. Действие звена 1 и стойки 0 заменяем реакциями 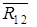 и
и 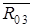 . Реакцию
. Реакцию 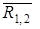 разложим на 2 составляющие:
разложим на 2 составляющие:
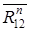 - по оси звена 2;
- по оси звена 2;
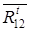 - перпендикулярно оси звена 2.
- перпендикулярно оси звена 2.
Составим уравнение равновесия вида (2) для звена 2:
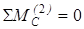 ;
; 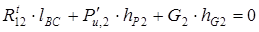 , (6)
, (6)
где плечи 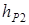 и
и 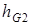 находим по чертежу:
находим по чертежу:
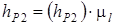 ;
; 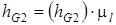
Из уравнения (6) находим: 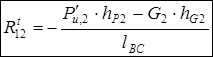 (н),
(н),
Аналогично поступаем со звеном 3.
Реакцию 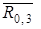 разложим на 2 составляющие:
разложим на 2 составляющие:
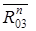 - по оси звена 3;
- по оси звена 3;
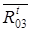 - перпендикулярно оси звена 3.
- перпендикулярно оси звена 3.
Составим уравнение равновесия вида (2) для звена 3:
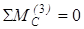 ;
; 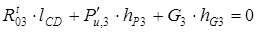 , (7)
, (7)
где плечи 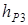 и
и 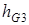 находим по чертежу:
находим по чертежу:
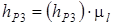 ;
; 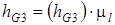
Из уравнения (7) находим:  (н)
(н)
Составляем уравнение вида (1) для группы:
 ;
; 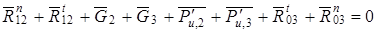 (8)
(8)
Строим план сил группы согласно уравнению (8) в выбранном масштабе 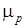 .
.
В результате построения плана сил находим величины 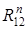 и
и 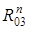 .
.
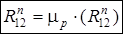 ;
; 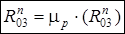 .
.
Полная реакция звена 1 на звено 2 равна геометрической сумме:
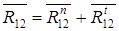 ;
; 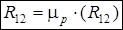 (н).
(н).
Полная реакция стойки на звено 3 равна:
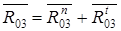 ;
; 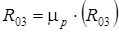 (н).
(н).
Определяем реакцию 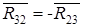 между звеньями 2 и 3. Для этого напишем уравнение вида (1) для звена 2.
между звеньями 2 и 3. Для этого напишем уравнение вида (1) для звена 2.
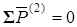 ;
; 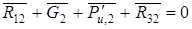 (9)
(9)
Строим план сил звена 2 согласно этому уравнению, из которого находим силу взаимодействия между звеньями 2 и 3.
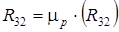 (Н).
(Н).
3.4. Силовой расчёт ведущего звена.
Изображаем звено 1 в положении, заданном для силового расчёта со всеми силами, действующими на него:
в точке В действует сила  (реакция от отброшенного звена 2, известная по величине и направлению из предыдущего расчёта);
(реакция от отброшенного звена 2, известная по величине и направлению из предыдущего расчёта);
в точке В действует сила  (реакция от отброшенного звена 4, известная по величине и направлению из предыдущего расчёта);
(реакция от отброшенного звена 4, известная по величине и направлению из предыдущего расчёта);
в точке В действует уравновешивающая сила  , направленная перпендикулярно звену 1 (пока неизвестной величины);
, направленная перпендикулярно звену 1 (пока неизвестной величины);
в точке А действует реакция 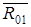 , неизвестная по величине и направлению.
, неизвестная по величине и направлению.
Из уравнения вида (2), составленного для звена 1, находим  по формуле
по формуле
 , т.е.
, т.е. 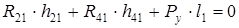 ,
,
откуда 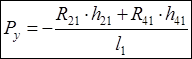 (н),
(н),
где 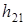 и
и 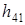 (плечи сил
(плечи сил  и
и  ) находятся по чертежу с учётом масштабного коэффициента:
) находятся по чертежу с учётом масштабного коэффициента:
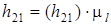 (м),
(м), 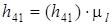 (м).
(м).
Составляем уравнение равновесия вида (1) для звена 1
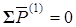 , т.е.
, т.е. 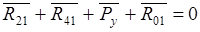
Строим план сил согласно этому уравнению и находим из него величину и направление реакции 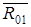 по формуле
по формуле
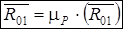 (н).
(н).
3.5. Определение уравновешивающей силы Ру методом Н.Е. Жуковского.
Переносим с листа № 1 на лист № 2 план скоростей механизма в положении, заданном для силового расчёта.
Находим на плане скоростей точки 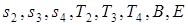 , соответствующие местам приложения внешних сил
, соответствующие местам приложения внешних сил 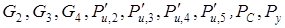 .
.
Переносим эти силы с плана механизма в соответствующие точки плана скоростей, предварительно повернув каждую сил в одну и ту же сторону на 90º.
Принимаем план скоростей за жёсткий рычаг с опорой в полюсе “ р ”, и записываем уравнение равновесия этого рычага 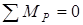 . При этом длины плеч берём с плана скоростей прямо в мм. Учитывая, что момент от силы
. При этом длины плеч берём с плана скоростей прямо в мм. Учитывая, что момент от силы 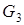 равен нулю (т.к. его плечо равно нулю), имеем:
равен нулю (т.к. его плечо равно нулю), имеем:
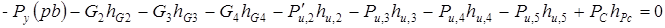
Откуда находим величину 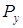 :
:
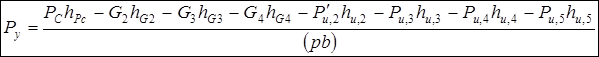 (Н).
(Н).
Определяем погрешность определения Ру методом планов сил и методом рычага Н.Е. Жуковского:
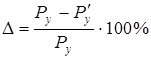
Расхождение не должно превышать (5 – 8) %.
Расчёт маховика.
На листе №3 изображаются:
1. График приведенных моментов инерции  ;
;
2. График приведенных моментов сил  ;
;
3. График работ сил сопротивления и движущих сил  и
и  ;
;
4. График избыточной работы  ;
;
5. График приращения кинетической энергии в функции от приведенного момента инерции (диаграмма энергомасс)  .
.
6. Эскиз маховика.
4.1. Построение графика приведенных моментов инерции  .
.
Из теории известно, что все реальные массы и моменты инерции звеньев механизма можно заменить эквивалентным моментом инерции 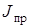 , которым как бы обладает звено приведения (кривошип).
, которым как бы обладает звено приведения (кривошип).
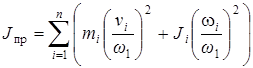 (10)
(10)
где: 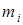 - масса звена i;
- масса звена i;
 - скорость центра масс звена i;
- скорость центра масс звена i;
 - момент инерции звена i относительно оси, проходящей через его центр масс;
- момент инерции звена i относительно оси, проходящей через его центр масс;
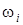 - угловая скорость звена i;
- угловая скорость звена i;
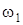 - угловая скорость звена приведения;
- угловая скорость звена приведения;
п – число подвижных звеньев;
Используя данные кинематического анализа (лист №1), вычисляем величину 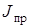 для 12 положений механизма. Для этого:
для 12 положений механизма. Для этого:
1. вычисляем постоянные величины, входящие в формулу (1):
 ,
, 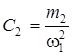 …,
…, 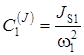 ,
, 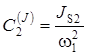 …
…
2. Составляем таблицу для будущего графика 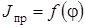 :
:
Таблица 7. Данные для построения графика 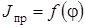 .
.
| Положения механизма | … | |||||

|
|
|
|


