 |
Свойства прямоугольного проецирования.
|
|
|
|
Свойства прямоугольного проецирования.
- Проекция точки есть точка
- В общем случае проекция прямой есть прямая линия, проекция кривой линии – кривая
- Свойство принадлежности фигур Ф и Ф1: Если Ф1 с Ф, то Ф1’ с Ф’
- Параллельные прямые проецируются в параллельные прямые
- Сохраняется просто отношение трех точек AB/BC = A’B’/B’C’
Какие линии называются линиями уровня?
Линиями уровня называются прямые, параллельные одной из плоскостей проекции.
Какие линии называются проецирующими линиями?
Проецирующие прямые — прямые, перпендикулярные плоскости проекции. На соответствующую плоскость проекции эти прямые проецируются в точку. На одну из плоскостей проекции они проецируются в натуральную величину.
Какая линия, принадлежащая плоскости, называется горизонталью? Приведите пример.
Горизонталью плоскости называется прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекций, обозначаемая h. Построение горизонтали начинается с фронтальной проекции h2. Все горизонтали одной плоскости между собой параллельны. Горизонталь есть геометрическое место точек плоскости, удаленных от плоскости p1 на одно и то же расстояние

Какая линия, принадлежащая плоскости, называется фронталью? Приведите пример.
Фронталью плоскости называется прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций, обозначаемая f. Все фронтали одной плоскости параллельны между собой. Фронталь плоскости – это геометрическое место точек, удаленных от плоскости p2 на одно и то же расстояние

Правило построения проекций точки, принадлежащей плоскости. Приведите пример.
|
|
|
Для того чтобы построить проекцию точки, принадлежащей плоскости общего положения, надо воспользоваться проекцией прямой, принадлежащей заданной плоскости и проходящей через точку.

Теорема о проецировании прямого угла.
Если одна сторона прямого угла параллельна плоскости проекции, а другая не перпендикулярна, то прямой угол проецируется на данную плоскость без искажений

На основании каких положений строят на чертеже параллельные, прямую и плоскость?
- Признак параллельности прямой и плоскости
- Свойство прямоугольного проецирования

На основании каких положений строят на чертеже две параллельные плоскости?
Построение на чертеже параллельных плоскостей основано на
- Признак параллельности двух плоскостей (если две пересекающаяся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
- Свойство прямоугольного проецирования о проекциях параллельных прямых.
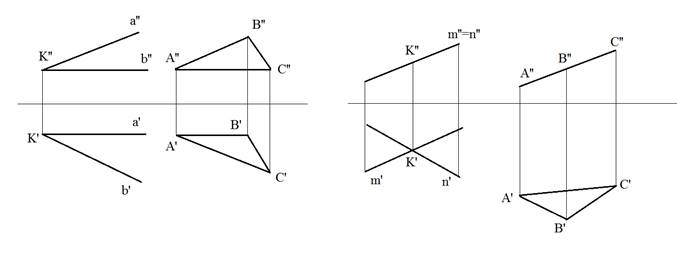
На основании каких положений строят на чертеже перпендикулярные: прямую и плоскость?
Построение на чертеже перпендикулярных прямой и плоскости
- Признаке перпендикулярности прямой и плоскости
- Теореме о проецировании прямого угла

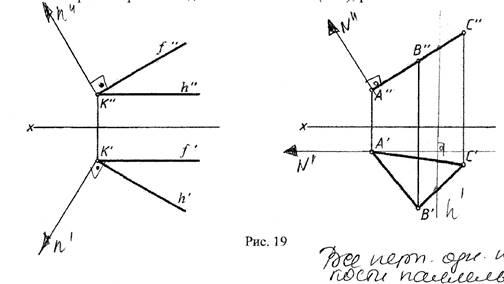
На основании каких положений строят на чертеже две перпендикулярные плоскости?
Построение на чертеже перпендикулярных плоскостей основано на:
- Признаке перпендикулярности двух плоскостей
- Теореме о проецировании прямого угла
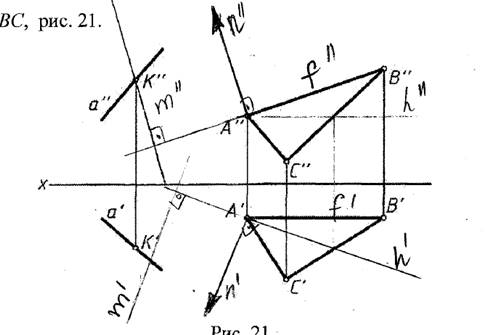
Последовательность построения точки пересечения прямой и плоскости.
1. Заключим прямую a во вспомогательную фронтально-проецирующую плоскость (плоскость перпендикулярную фронтальной плоскости проекции). На фронтальной проекции она совпадает с прямой а. m – линия пересечения этой плоскости с плоскостью треугольника ABC на фронтальной проекции так же будет совпадать с прямой a (a''=m'')
|
|
|
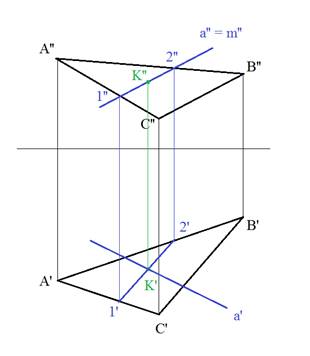
2. Определим фронтальные проекции 2 точек этой линии: 1 и 2
3. Найдем их горизонтальные проекции
4. Соединим горизонтальные проекции точек 1 и 2 – горизонтальная проекция прямой m, которая является точкой пересечения вспомогательной плоскости с плоскостью треугольника АВС и соответственно принадлежит обеим плоскостям. Так как прямая а и m принадлежит вспомогательной плоскости, то точка пересечения этих прямых k – точка пересечения прямой а с плоскостью треугольника АВС.
5. С помощью линии связи найдем фронтальную проекцию точки пересечения k.
|
|
|


